Grade 9 Exam > Grade 9 Notes > AP Statistics > Chapter Notes: Overview: Exploring Two-Variable Data
Overview: Exploring Two-Variable Data Chapter Notes | AP Statistics - Grade 9 PDF Download
Welcome to Unit 2 of AP Statistics! This unit dives into the analysis of relationships between two variables, helping you understand how to visualize, describe, and interpret data connections using tools like scatterplots, correlation, and regression models. Let’s break it down into manageable pieces with examples to guide you!
What You’ll Learn
- Scatterplots: Create and analyze scatterplots to spot patterns and trends in two-variable data.
- Correlation: Understand the correlation coefficient, which quantifies the strength and direction of a linear relationship between two variables.
- Least-Squares Regression: Learn to find the best-fit line for data and use it to predict outcomes.
- Interpreting Regression Lines: Decode the slope and y-intercept of a regression line to understand variable relationships and make predictions.
- Evaluating Linear Models: Assess how well a linear model fits the data.
- Residual Plots: Use residual plots to determine if a linear model is appropriate for describing data relationships.
Don’t worry if this feels overwhelming—this unit is broken into bite-sized sections with plenty of examples to make it clear!
Exam Weighting
- Accounts for 5–7% of the AP Statistics exam.
- Expect 2–3 multiple-choice questions.
- May include one Free Response Question (FRQ) or part of an investigative task.
Bivariate Data: Categorical vs. Quantitative
After mastering single-variable statistics, Unit 2 steps up to bivariate data, which involves two variables. These can be either categorical or quantitative, each requiring different analysis methods.
Categorical Data
Categorical bivariate data is analyzed using two-way tables to explore relationships between two categorical variables. For example, you might examine a dataset comparing students’ class levels (e.g., freshman, sophomore) with their preferred learning mode (virtual or in-person) for the 2020–2021 school year. This setup helps statisticians identify potential correlations between the variables.
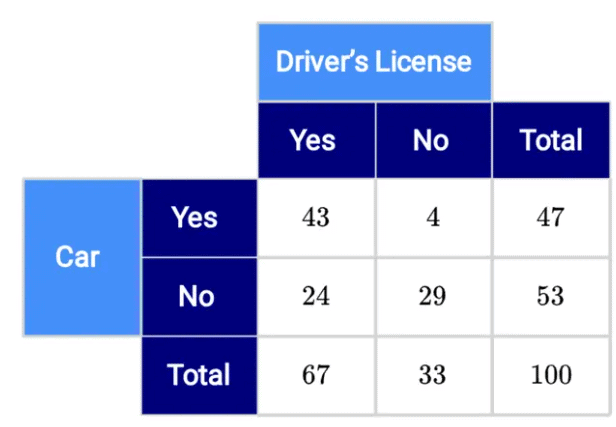
Quantitative Data
Quantitative bivariate data is visualized using scatterplots, with one variable (independent) plotted on the x-axis and the other (dependent) on the y-axis. For instance, plotting height (x-axis) against shoe size (y-axis) might reveal a positive correlation, where taller individuals tend to have larger shoe sizes. Linear regression models are often used to fit a line to the scatterplot, enabling predictions within the data range.
Computer Outputs
Rather than creating scatterplots or regression models from scratch, the AP exam typically provides computer-generated outputs (e.g., scatterplots, two-way tables, or regression models) for interpretation. Your key skill is understanding and explaining these outputs in context, including elements like slope, y-intercept, correlation coefficient, and coefficient of determination for regression models, or joint, marginal, and conditional relative frequencies for categorical data.

Mathematical Practices
This unit incorporates three College Board mathematical practices:
- Selecting Statistical Methods: Choose appropriate methods for analyzing two-variable data, distinguishing between categorical and quantitative approaches.
- Data Analysis: Calculate statistics, create models, and draw conclusions from bivariate datasets.
- Statistical Argumentation: Build arguments about variable relationships, remembering that correlation does not imply causation. For example, if rainfall is higher on Tuesdays than Mondays, it doesn’t mean the day of the week causes more rain—correlation exists, but not causation.
Main Concepts
- Categorical Variables: Two-way tables, joint/marginal/conditional relative frequencies, side-by-side bar graphs, segmented bar graphs, mosaic plots.
- Quantitative Variables: Scatterplots (form, direction, strength, unusual features like gaps, clusters, outliers), correlation coefficient, linear regression, residuals, r, R², s, extrapolation, influential points, data transformations.
Question for Chapter Notes: Overview: Exploring Two-Variable DataTry yourself: What type of data is analyzed using two-way tables?View Solution
Key Terms to Know
- Bivariate Data: Data involving two variables, used to study their relationship and identify patterns or trends.
- Categorical Variables: Non-numerical data representing categories, like gender or class level, used for grouping and comparison.
- Categorical Data Methods: Techniques for analyzing categorical data, focusing on relationships and patterns within groups.
- Conditional Relative Frequencies: Proportions of outcomes within a specific subgroup, revealing relationships between categorical variables.
- Correlation Coefficient: A value (-1 to 1) measuring the strength and direction of a linear relationship between two quantitative variables.
- Correlation Does Not Imply Causation: A reminder that a relationship between variables doesn’t mean one causes the other.
- Data Analysis: Applying statistical techniques to summarize, interpret, and draw conclusions from data.
- Extrapolation: Predicting values beyond the observed data range, often less reliable than interpolation.
- Intercept: The y-axis point where a regression line crosses, representing the dependent variable’s value when the independent variable is zero.
- Linear Regression Models: Methods to predict a dependent variable using one or more independent variables via a linear equation.
- Least-Squares Regression: A linear regression method that minimizes the sum of squared residuals to find the best-fit line.
- Marginal Relative Frequencies: Proportions of a category relative to the total dataset in a contingency table.
- Mosaic Plots: Visuals showing relationships between two categorical variables using proportional rectangles.
- Quantitative Data Methods: Techniques for analyzing numerical data to identify patterns and make predictions.
- Quantitative Variables: Measurable data expressed numerically, suitable for calculations and regressions.
- R, R², and s: r (correlation coefficient), R² (proportion of variance explained), s (standard deviation of residuals).
- Regression Equation: A formula describing the relationship between dependent and independent variables for predictions.
- Residuals: Differences between observed and predicted values, used to assess a regression model’s fit.
- Scatterplots: Graphs plotting two quantitative variables to visualize their relationship and trends.
- Segmented Bar Graphs: Bar graphs divided into segments to show categorical data proportions within a group.
- Side-by-Side Bar Graphs: Bar graphs comparing categorical variables side by side to highlight differences.
- Slope: The rate of change in a regression line, showing how the dependent variable changes per unit of the independent variable.
- Statistical Argumentation: Using data to support or refute claims, emphasizing contextual interpretation.
- Strength: The degree of correlation between variables, indicating how well one predicts the other.
- Two-Variable Statistics Methods: Techniques to analyze relationships between two quantitative variables.
- Unusual Features (Gaps, Clusters, Outliers): Distinct data characteristics like gaps (no data), clusters (grouped data), or outliers (extreme values).
The document Overview: Exploring Two-Variable Data Chapter Notes | AP Statistics - Grade 9 is a part of the Grade 9 Course AP Statistics.
All you need of Grade 9 at this link: Grade 9
|
12 videos|106 docs|12 tests
|
FAQs on Overview: Exploring Two-Variable Data Chapter Notes - AP Statistics - Grade 9
| 1. What is the difference between categorical and quantitative data in bivariate analysis? |  |
Ans.Categorical data refers to variables that can be divided into groups or categories, such as gender or color, while quantitative data involves numerical values that can be measured, such as height or weight. In bivariate analysis, understanding the type of data helps determine the appropriate statistical methods to use.
| 2. How can I interpret computer outputs for bivariate data on the AP Exam? |  |
Ans.Computer outputs often include regression analysis, correlation coefficients, and graphical representations. To interpret these outputs, focus on the significance of p-values, the strength and direction of correlations, and any trends in scatterplots. Understanding these elements will help answer related questions on the exam.
| 3. What mathematical practices should I focus on for the AP Exam regarding two-variable data? |  |
Ans.Focus on practices such as making sense of problems, reasoning abstractly and quantitatively, constructing viable arguments, and modeling with mathematics. These practices will enhance your ability to analyze data and apply mathematical concepts effectively during the exam.
| 4. What are the main concepts to understand when exploring two-variable data? |  |
Ans.Key concepts include understanding relationships between variables, recognizing patterns in data, and using statistical measures like correlation and regression. Familiarity with these concepts will help you analyze bivariate data and answer exam questions accurately.
| 5. How does exam weighting impact the preparation for the AP Exam in statistics? |  |
Ans.Exam weighting indicates the relative importance of different sections. By understanding which topics carry more weight, students can prioritize their study time effectively, focusing on areas that will have a greater impact on their overall exam scores.
Related Searches















