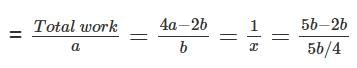Important Formulas: Pipes and Cisterns | Quantitative Aptitude (Quant) - CAT PDF Download

Pipes and cisterns problems involve calculating the time taken to fill or empty a tank using pipes, which are classified as inlets (pipes that fill the tank) or outlets (pipes that empty the tank).
These problems are conceptually similar to time and work problems, where the "work" is the volume of the tank filled or emptied, and the "time" is how long it takes to complete this task.
Key Concepts
Inlet: A pipe that fills a tank.
Outlet: A pipe that empties a tank.
Work Rate: The fraction of the tank filled or emptied per unit of time (usually per hour).
Net Rate: When multiple pipes are open simultaneously, the net rate is the sum of the individual rates, accounting for whether they fill (positive rate) or empty (negative rate) the tank.
Important Formulas
1) If an inlet connected to a tank fills it in X hours, part of the tank filled in one hour is =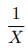
2) If an outlet connected to a tank empties it in Y hours, part of the tank emptied in one hour is =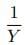
3) An inlet can fill a tank in X hours and an outlet can empty the same tank in Y hours.
- If both the pipes are opened at the same time and Y > X, the net part of the tank filled in one hour is given by=
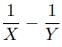
Therefore, when both the pipes are open the time taken to fill the whole tank is given by= Hours
Hours - If X is greater than Y, more water is flowing out of the tank than flowing into the tank. And, the net part of the tank emptied in one hour is given by=
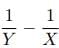
Therefore, when both the pipes are open the time taken to empty the full tank is given by=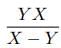 Hours
Hours
4) An inlet can fill a tank in X hours and another inlet can fill the same tank in Y hours. If both the inlets are opened at the same time, the net part of the tank filled in one hour is given by=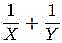
Therefore, the time taken to fill the whole tank is given by= 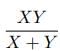 Hours
Hours
Solved Examples
Q1: Two pipes A and B are attached to an empty water tank. Pipe A fills the tank while pipe B drains it. If pipe A is opened at 2 pm and pipe B is opened at 3pm, then the tank becomes full at 10 pm. Instead, if pipe A is opened at 2 pm and pipe B is opened at 4 pm, then the tank becomes full at 6 pm. If pipe B is not opened at all, then the time, in minutes, taken to fill the tank is: (CAT 2021 Slot 2)
A: 140
B: 120
C: 144
D: 264
Ans: A
Sol:
Let the filling and emptying capacity of A and B be 'a' and 'b' units/hour respectively.
Case 1: A is opened at 2 pm and B at 3 pm
Total work done till 10 pm = 8a - 7b
Case 2: A is opened at 2 pm and B at 4 pm
Total work done till 6 pm = 4a - 2b
As work done is same for A and B
8a -7b = 4a - 2b
4a = 5b
Now time taken by A alone to fill the tank
= 12/5 hours = 144 minutes.
Q2: A water tank has inlets of two types A and B. All inlets of type A when open, bring in water at the same rate. All inlets of type B, when open, bring in water at the same rate. The empty tank is completely filled in 30 minutes if 10 inlets of type A and 45 inlets of type B are open, and in 1 hour if 8 inlets of type A and 18 inlets of type B are open. In how many minutes will the empty tank get completely filled if 7 inlets of type A and 27 inlets of type B are open? (CAT 2018 Slot 2)
Ans: 48
Sol:
Suppose the inlet pipes of type A fill in water at the rate 'a' units per minute and the inlet pipes of type B fill in water at the rate 'b' units per minute.
Therefore we have the following
30(10a + 45b) = 60(8a + 18b)
300a + 1350b = 480a + 1080b
180a = 270b
a = 1.5b
Total capacity of the tank
300a + 1350b = 300(1.5b) + 1350b = 1800b
If 7 inlet pipes of type A and 27 inlet pipes of type B are opened, the volume of water filled in every minute
7a + 27b = 7(1.5b) + 27b = 37.5b
Therefore the number of minutes taken to fill the tank = 1800/37.5 = 48
Q3: A tank has an inlet pipe and an outlet pipe. If the outlet pipe is closed then the inlet pipe fills the empty tank in 8 hours. If the outlet pipe is open then the inlet pipe fills the empty tank in 10 hours. If only the outlet pipe is open then in how many hours the full tank becomes half-full? (CAT 2017 Slot 2)
A: 20
B: 30
C: 40
D: 45
Ans: A
Sol:
The Inlet pipe will fill 1/8th of the tank in an hour.
The outlet pipe will empty the tank in 10 hours.
Outlet pipe will empty 1/10th of the tank.
1/8 - 1/B = 1/100
10(B-8) =8B
B= 40
Outlet pipe will take 40 hours to empty the tank fully
So, to half empty the tank, it will take 20 hours.
Q4: A chemical plant has four tanks (A, B, C, and D), each containing 1000 litres of a chemical. The chemical is being pumped from one tank to another as follows:
From A to B @ 20 litres/minute,
From C to A @ 90 litres/minute,
From A to D @ 10 litres/minute,
From C to D @ 50 litres/minute,
From B to C @ 100 litres/minute,
From D to B @ 110 litres/minute.
Which tank gets emptied first and how long does it take (in minutes) to get empty after pumping starts? (CAT 2005)
A: A, 16.66
B: C, 20
C: D, 20
D: D, 25
Ans: C
Sol:
The change in the amount of chemical in each tank after every minute is as follows:
A: -20 - 10 + 90 = 60
B: -100 + 110 + 20 = 30
C: -50 - 90 + 100 = -40
D: -110 + 10 + 50 = -50
Since tank D loses the maximum amount of chemical in a minute, it will be emptied first
Let n minutes be the time taken by tank D to get empty.
1000 - 50n = 0
n = 20 minutes
Q5: Two full tanks, one shaped like a cylinder and the other like a cone, contain jet fuel. The cylindrical tank holds 500 L more than the conical tank. After 200 L of fuel has been pumped out from each tank, the cylindrical tank contains twice the amount of fuel in the conical tank. How many litres of fuel did the cylindrical tank have when it was full? (CAT 2000)
A: 700L
B: 1000L
C: 1100L
D: 1200L
Ans: D
Sol:
Let the conical tank hold x L of fuel, then cylindrical tank will hold = (x + 500) L
Given, (x + 300) = 2(x − 200)
⇒ x = 700 L
Hence, cylindrical tank will hold (700 + 500) = 1200 L of fuel.
Example 6: A water tank has three taps A, B and C. A fills four buckets in 24 minutes, B fills 8 buckets in 1 hour and C fills 2 buckets in 20 minutes. If all the taps are opened together, a full tank is emptied in 2 hours. If a bucket can hold 5 liters of water, what is the capacity of the tank?
A: 120 liters
B: 240 liters
C: 180 liters
D: 60 liters
Ans: B
Solution: A fills 4 buckets in 24 minutes. Thus, A fills 1 bucket in 24/4 = 6 minutes
Similarly, B fills 8 buckets in 1 hour. Thus B fills 1 bucket in 60/8 minutes
Similarly, C fills one bucket in 20/2 = 10 minutes
In 2 hours,
Number of buckets filled by A will be = 120/6 = 20 buckets
Number of buckets filled by B will be = 120/ (60/8) = (120 * 8) / 60 = 16 buckets
Number of buckets filled by C will be = 120 / 10 = 12 buckets
Total number of buckets filled = (20 + 16 + 12) = 48 buckets
Total amount of water coming out of the tank = capacity of the tank = 48 * 5 liters = 240 liters
Example 7: There is a leak in the bottom of the tank. This leak can empty a full tank in 8 hours. When the tank is full, a tap is opened into the tank which admit 6 liters per hour and the tank is now emptied in 12 hours. What is the capacity of the tank?
A: 8.8 liters
B: 36 liters
C: 144 liters
D: Cannot be determined
Ans: 24 minutes
Solution: Since the leak can empty the tank in 8 hours,
In one hour, part of the tank emptied by the leak = 1/8
Also, after opening the tap, in one hour, part of the tank emptied = 1/12
Let the tap can fill the tank in x hours. Therefore, In one hour, part of the tank filled by the tap = 1/x
As per question, (1/x) – (1/8) = 1/12
Or x = 24
Since the tap admits 6 liters of water per hour, it will admit (6*24) =144 liters of water in 24 hours, which should be the capacity of the tank.
Example 8: Three small pumps and one large pump are filling a tank. Each of the three small pump works at 2/3 of the rate of the large pump. If all four pumps work at the same time, they should fill the tank in what fraction of the time that it would have taken the large pump alone?
A: 4/7
B: 1/3
C: 2/3
D: ¾
Ans: B
Solution: As per the question,
Capacity of three small pumps = Capacity of two large pumps
Also, if we want to express the capacity of three small pumps + one large pump in terms of large pump, we should add one large pump on both sides of the above equation
Adding one large pump on both sides of the above equation, we get
Three small pumps + one large pump = Three large pumps.
Thus, if all the four pumps are open together, they would fill the tank in 1/3 rd of the time large pump would have taken alone.
Example 9: A tank is fitted with 8 pipes, some of which that fill the tank and others that empty the tank. Each of the pipes that fills the tank fills it in 8 hours, while each of those that empty the tank empties it in 6 hours. If all the pipes are kept open when the tank is full, it will take 6 hours to drain the tank. How many of these are fill pipes?
A: 2 fill pipes
B: 4 fill pipes
C: 6 fill pipes
D: 5 fill pipes
Ans: B
Solution: Let the number of fill pipes be ‘n’
Therefore, there will be (8 – n) waste pipes.
Each of the fill pipes can fill the tank in 8 hours.
Therefore, each of the fill pipes will fill 1/8th of the tank in an hour.
Hence, n fill pipes will fill n/8th of the tank in an hour.
Similarly, each of the waste pipes will drain the full tank in 6 hours.
∴ each of the waste pipes will drain 1/6th of the tank in an hour.
(8 – n) waste pipes will drain (8-n)/6th of the tank in an hour.
Between the fill pipes and the waste pipes, they drain the tank in 6 hours.
That is, when all 8 of them are opened, 1/6th of the tank gets drained in an hour.
(Amount of water filled by fill pipes in 1 hour – Amount of water drained by waste pipes 1 hour) = (1/6th ) of the tank
Therefore,
(n/8) – ((8−n)/)6 = -1/6
Note: The right hand side has a negative sign because the tank gets drained.
Cross multiplying and solving the equations, 14n – 64 = -8
or 14n = 56 or n = 4
Example 10: Pipe A usually fills a tank in 2 hours. On account of a leak at the bottom of the tank, it takes pipe A 30 more minutes to fill the tank. How long will the leak take to empty a full tank if pipe A is shut?
A: 2 hours 30 minutes
B: 5 hours
C: 4 hours
D: 10 hours
Ans: D
Solution: Pipe A fills the tank normally in 2 hours.
Therefore, it will fill 1/2 of the tank in an hour.
Let the leak take x hours to empty a full tank when pipe A is shut.
Therefore, the leak will empty 1/x of the tank in an hour.
The net amount of water that gets filled in the tank in an hour when pipe A is open and when there is a leak = (1/2 – 1/x) of the tank. —– (1)
Now, when there is a leak, the problem states that it takes two and a half hours to fill the tank. i.e. 5/2hours.
Therefore, in an hour, 2/5th of the tank gets filled. —– (2)
Equating (1) and (2), we get 1/2 – 1/x = 2/5
=> 1/x = 1/2 – 2/5 = 1/10
=> x = 10 hours.
|
167 videos|229 docs|95 tests
|
FAQs on Important Formulas: Pipes and Cisterns - Quantitative Aptitude (Quant) - CAT
| 1. What are the basic concepts of pipes and cisterns in mathematics? |  |
| 2. What formulas are commonly used in solving pipes and cisterns problems? |  |
| 3. How do you solve a problem involving two pipes filling a cistern together? |  |
| 4. Can you explain a common example of a pipes and cistern problem? |  |
| 5. What strategies can be used to tackle complex pipes and cisterns problems in exams like CAT? |  |