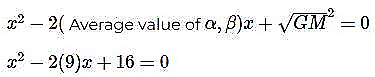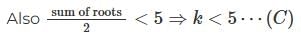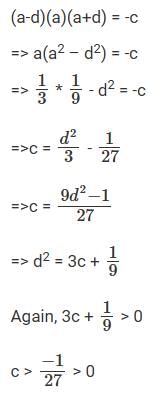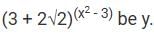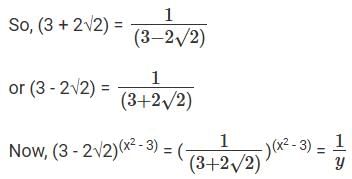Solved Examples: Quadratic Equations | Quantitative Aptitude (Quant) - CAT PDF Download

Q1: The difference between the corresponding roots of x² + ax + b = 0 and x² + bx + a = 0 is the same and a ≠ b, then
A: a + b + 4 = 0
B: a + b − 4 = 0
C: a − b − 4 = 0
D: a − b + 4 = 0
Ans: A
Sol:
Let α, β be the roots of x² + bx + a = 0.
Therefore, α + β = −b and αβ = a.
Let γ, δ be the roots of x² + ax + b = 0.
Therefore, γ + δ = −a and γδ = b.
Given that α − β = γ − δ,
we have:
(α − β)² = (γ − δ)²
⇒ (α + β)² − 4αβ = (γ + δ)² − 4γδ
⇒ b² − 4a = a² − 4b
⇒ b² − a² = −4(b − a)
⇒ (b − a)(b + a + 4) = 0
Since a ≠ b, we get b + a + 4 = 0.
Hence, the correct option is A.
Q2: The number of real solutions of the equation x² − 3|x| + 2 = 0 is
A: 4
B: 1
C: 3
D: 2
Ans: A
Sol:
Given x² − 3|x| + 2 = 0.
If x ≥ 0, then |x| = x, and the equation becomes x² − 3x + 2 = 0.
⇒ (x − 1)(x − 2) = 0
⇒ x = 1, 2
If x < 0, x² - 3|x| + 2 = 0.
the equation becomes x² + 3x + 2 = 0.
⇒ (x + 1)(x + 2) = 0
⇒ x = −1, −2
Hence, the solutions are x = 1, −1, 2, −2, giving four real solutions.
Q3: Let two numbers have arithmetic mean 9 and geometric mean 4. Then these numbers are the roots of the quadratic equation
A: x² + 18x − 16 = 0
B: x² − 18x + 16 = 0
C: x² + 18x + 16 = 0
D: x² − 18x − 16 = 0
Ans: B
Sol:
Let the two numbers be α, β.
Given: (α + β)/2 = 9 and √(αβ) = 4.
Therefore, Required equation
Q4: If both the roots of the quadratic equation x² − 2kx + k² + k − 5 = 0 are less than 5, then k lies in the interval
A: (6, ∞)
B: (5, 6]
C: [4, 5]
D: (−∞, 4)
Ans: D
Sol:
Given x² - 2kx + k² + k - 5 = 0
Roots are less than 5 ⇒ D ≥ 0
⇒ (-2k)² ≥ 4(k² + k - 5) ⇒ k ≤ 5 ... (A)
Again f(5) > 0
⇒ 25 - 10k + k² + k - 5 > 0
⇒ k² - 9k + 20 > 0 ⇒ (k - 4)(k - 5) > 0
⇒ k < 4 ∪ k > 5 ... (B)from (A),(B),(C) we have k∈(−∞,4) as the choice gives number k<5
Q5: The quadratic equations x² − 6x + a = 0 and x² − cx + 6 = 0 have one root in common. The other roots of the first and second equations are integers in the ratio 4:3. Then the common root is
A: 2
B: 1
C: 4
D: 3
Ans: A
Sol:
Let α and 4β be the root of
x² - 6x + a = 0
and α and 3β be those of the equation
x² - cx + 6 = 0
From the relation between roots and coefficients
α + 4β = 6 and 4αβ = a
α + 3β = c and 3αβ = 6
we obtain αβ = 2 giving a = 8
The first equation is x² - 6x + 8 = 0 ⇒ x = 2, 4
For α = 4, 4β = 2 ⇒ 3β = 3/2 (not an integer)
So the common root is α = 2
Q6: What is the number of real solutions of the equation x2 - 7|x| - 18 = 0?
A: 2
B: 4
C: 3
D: 1
Ans: A
Sol:
Let us split this into two cases. Case 1, when x is greater than 0 and Case 2, when x is lesser than 0.
Case 1
x < 0. Now, |x| = x
x2 – 7x – 18 = 0
(x – 9) (x + 2) = 0
x is either –2 or +9.
Case 2
x < 0. Now, |x| = –x
x2 + 7x – 18 = 0
(x + 9) (x – 2) = 0
x is either –9 or +2.
However, in accordance with the initial assumption that x < 0, x can only be –9 (cannot be +2).
Hence, this equation has two roots: –9 and +9.Alternatively, we can treat this as a quadratic in |x|, the equation can be written as |x|2 – 7 |x| – 18 = 0.
Or, (|x| – 9) (|x| + 2) = 0
|x| = 9 or –2. |x| cannot be –2.
S|x| = 9, x = 9 or –9.
Q7: The equation x² - 9x + k = 0 has real roots. How many integer values can 'k' take?
A: 40
B: 21
C: 20
D: 41
Ans: D
Sol:
Discriminant, D = 81 – 4|k|
If roots are real, D > 0
81 – 4|k| > 0
4|k| < 81
|k| < 20.25
Hence, –20.25 < k < 20.25
The integer values that k can take are –20, –19, –18 … 0 … 18, 19 and 20.
41 different values (Remember to include 0.)
Q8: Let x³ - x² + bx + c = 0 have 3 real roots which are in A.P. Which of the following could be true?
A: b = 2, c = 2
B: b = 1, c = 1
C: b = -1, c = 1
D: b = -1, c = -1
Ans: B
Sol:
Given the roots are in A.P. so let a-d, a, a+d be the roots
From equation, sum of roots = 1
Sum of two roots taken at a time = +b
Product of two roots = -c
∴ (a-d)+ (a)+ (a+d) = 1
⇒ 3a = 1
⇒ a = 1/3
Also, (a-d)a + a(a+d) + (a-d)(a+d) = b
⇒ a² - ad + a² + ad + a² - d² = b
⇒ 3a² - d² = b
⇒ 3 * 1/9 - d² = b
⇒ d² = b - 1/3
Now, since d is a real number,
1/3 - b > 0 => b < 1/3
Also,
Q9: (3 + 2√2)(x² - 3) + (3 - 2√2)(x² - 3) = b which of the following can be the value of b?
A: 2
B: √2
C: -√2
D: All the above
Ans: A
Sol:
(3 + 2√2) and (3 - 2√2) are conjugate numbers. Since they are conjugate numbers,(3 + 2√2) * (3 - 2√2) = 1
Equation can be written as:-
As a rule, the expression:
From the options, it is clear that y+ 1/y can take the value 2.
So, b can take the value 2.
Q10: If f(y) = x2 + (2p + 1)x + p2 - 1 and x is a real number, for what values of ‘p' the function becomes 0?
A: p > 0
B: p > -1
C: p ≥ -5/4
D: p ≤ 3/4
Ans: C
Sol:
The function f(y) is a quadratic equation.
It is given that x is real.
So the discriminant of f(y) ≥ 0
i.e. D = b2 - 4ac ≥ 0 or
(2p + 1)2 – 4(p2 - 1) ≥ 0
4p2 + 4p + 1 – 4 (p2 - 1) ≥ 0
4p + 5 ≥ 0
Or p ≥ −5/4
Choice C is the correct answer.
|
184 videos|212 docs|103 tests
|
FAQs on Solved Examples: Quadratic Equations - Quantitative Aptitude (Quant) - CAT
| 1. What are quadratic equations and how are they defined? |  |
| 2. How can I solve a quadratic equation using the quadratic formula? |  |
| 3. What is the significance of the discriminant in a quadratic equation? |  |
| 4. can you explain how to factor a quadratic equation? |  |
| 5. what methods can be used to solve quadratic equations besides the quadratic formula? |  |
| 4.="" can="" you="" explain="" how="" to="" factor="" a="" quadratic="" equation?="" |  |
| 5.="" what="" methods="" can="" be="" used="" to="" solve="" quadratic="" equations="" besides="" the="" quadratic="" formula?="" |  |
| 4. can you explain how to factor a quadratic equation? |  |
| 5. what methods can be used to solve quadratic equations besides the quadratic formula? |  |