Important Formulas: Divisibility & Remainder | Quantitative Aptitude (Quant) - CAT PDF Download
| Table of contents |

|
| Introduction |

|
| Divisibility Rules |

|
| Factors and Multiples |

|
| GCD and LCM |

|
| Modular Arithmetic |

|
| Solved Examples |

|
Introduction
Divisibility and remainders are core concepts in number theory, essential for the quantitative aptitude section of the CAT. A number a is divisible by b if there exists an integer q such that a = b × q, leaving no remainder. When division results in a remainder, we express a = b × q + r, where 0 ≤ r < b. This guide covers divisibility rules, factor calculations, modular arithmetic, and their applications, with examples and practice questions tailored for CAT preparation.
Divisibility Rules
Divisibility rules allow quick checks to determine if a number is divisible by another without performing division. Below are key rules for CAT:
- Divisibility by 2: A number is divisible by 2 if its last digit is even (0, 2, 4, 6, or 8).Example: 124 is divisible by 2 (last digit is 4).
- Divisibility by 3: A number is divisible by 3 if the sum of its digits is divisible by 3.Example: For 123, sum = 1 + 2 + 3 = 6, divisible by 3, so 123 is divisible by 3.
- Divisibility by 4: A number is divisible by 4 if the number formed by its last two digits is divisible by 4.Example: For 1236, last two digits are 36, and 36 ÷ 4 = 9, so 1236 is divisible by 4.
- Divisibility by 5: A number is divisible by 5 if its last digit is 0 or 5.Example: 125 ends with 5, so it is divisible by 5.
- Divisibility by 6: A number is divisible by 6 if it is divisible by both 2 and 3.Example : 126 is even, and sum = 1 + 2 + 6 = 9, divisible by 3, so 126 is divisible by 6.
- Divisibility by 7: Multiply the last digit by 2, subtract from the remaining number, and check if the result is divisible by 7.Example: For 119, last digit = 9, 9 × 2 = 18, remaining = 11, 11 − 18 = −7, divisible by 7.
- Divisibility by 8: A number is divisible by 8 if its last three digits form a number divisible by 8.Example: For 99992, last three digits = 992, 992 ÷ 8 = 124, so 99992 is divisible by 8.
- Divisibility by 9: A number is divisible by 9 if the sum of its digits is divisible by 9.Example: For 12345, sum = 1 + 2 + 3 + 4 + 5 = 15, not divisible by 9.
- Divisibility by 10: A number is divisible by 10 if its last digit is 0.Example: 1230 ends with 0, so it is divisible by 10.
- Divisibility by 11: The difference between the sum of digits in odd positions and even positions must be a multiple of 11 (including 0).Example: For 12345, odd positions = 1 + 3 + 5 = 9, even positions = 2 + 4 = 6, difference = 9 − 6 = 3, not divisible by 11.
- Divisibility by 12: A number is divisible by 12 if it is divisible by both 3 and 4.Example: For 10032, sum = 1 + 0 + 0 + 3 + 2 = 6, divisible by 3; last two digits = 32, divisible by 4; so divisible by 12.
- Divisibility by 13: Add 4 times the last digit to the remaining number, repeat until a two-digit number, and check divisibility by 13.Example: For 4355, 5 × 4 = 20, 435 + 20 = 455, 5 × 4 = 20, 45 + 20 = 65, 65 ÷ 13 = 5, so divisible by 13.
Factors and Multiples
- A factor of a number n is a number that divides n without leaving a remainder.
- A multiple of n is obtained by multiplying n by an integer.
1. Number of Factors
For a number n = p1a1 × p2a2 × ... × pkak, where pi are primes and ai are their powers, the number of factors is: (a1 + 1)(a2 + 1)...(ak + 1).
For 72 = 23 × 32,
Number of factors = (3 + 1)(2 + 1) = 4 × 3 = 12.
Factors: 1, 2, 3, 4, 6, 8, 9, 12, 18, 24, 36, 72.
2. Sum of Factors
The sum of all factors is: 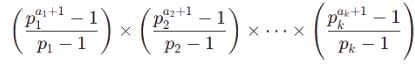
sum of factors
=
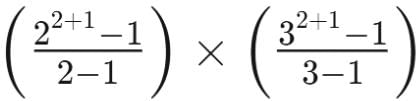
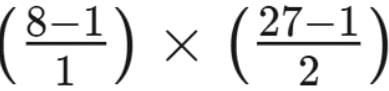 = 7 × 13 = 91
= 7 × 13 = 913. Product of Factors
The product of all factors is nt/2, where t is the number of factors.
For 36, t = (2+1)(2+1) = 9,
product = 369/2
= (364) × √36.
GCD and LCM
- The Greatest Common Divisor (GCD) is the largest number dividing two numbers. The Least Common Multiple (LCM) is the smallest number that is a multiple of both.
- Their relationship is:
GCD(a, b) × LCM(a, b) = a × b
Modular Arithmetic
Modular arithmetic deals with remainders. If a ≡ b (mod m), then m divides a − b.
Properties
- a + c ≡ b + d (mod m)
- a − c ≡ b − d (mod m)
- a × c ≡ b × d (mod m)
- ak ≡ bk (mod m)
Example: Find the remainder when 2100 is divided by 13.
Sol: Using Fermat’s Little Theorem: For prime p, if a is not divisible by p, then ap−1 ≡ 1 (mod p).
Here, p = 13, a = 2, so 212 ≡ 1 (mod 13).
Thus, 2100 = 212 × 8 + 4
= (212)8 × 24 ≡ 18 × 16 ≡ 16 (mod 13).
Since 16 − 13 = 3, the remainder is 3.
Solved Examples
Example 1: How many factors of the number 28 x 36 x 54 x 105 are multiples of 120?
a. 540
b. 660
c. 594
d. 792
Ans: Option 'c' is correct.
Sol: The prime factorization of 28 x 36 x 54 x 105 is 213 x 36 x 59.
Now, 120 can be prime-factorized as 23 x 3 x 5.
All factors of 213 x 36 x 59 that can be written as multiples of 120 will be of the form 23 x 3 x 5 x K.
213 x 36 x59 = 23 x 3 x 5 x K
=> K = 210x 35 x58.
The number of factors of N that are multiples of 120 is identical to the number of factors of K.
Number of factors of K = (10 + 1) (5 + 1) * (8 + 1) = 11 x 6 x 9 = 594
Example 2: Number N = 26 x 55 x 76 x 107; how many factors of N are even numbers?
a.1183
b. 1200
c. 1050
d. 540
Ans: Option 'a' is correct.
Sol: The prime factorization of 26 x 55 x 76 x 107 is 213 x 512 x 76.
The total number of factors of N = 14 x 13 x 7
We need to find the total number of even factors. For this, let us find the total number of odd factors and then subtract this from the total number of factors. Any odd factor will have to be a combination of powers of only 5 and 7.
Total number of odd factors of 213 x 512 x 76 = (12 + 1) x (6 + 1) = 13 x 7
Total number of factors = (13 + 1) x (12 + 1) x (6 + 1)
Total number of even factors = 14 x 13 x 7 - 13 x 7
Number of even factors = 13 x 13 x 7 = 1183
Example 3: If a three digit number ‘abc’ has 3 factors, how many factors does the 6-digit number ‘abcabc’ have?
a. 16 factors
b. 24 factors
c. 16 or 24 factors
d. 20 factors
Ans: Option 'c is correct
Sol: ‘abc’ has exactly 3 factors,
so ‘abc’ should be square of a prime number. (Important ot remember)
Any number of the form paqbrc will have (a + 1) (b + 1) (c + 1) factors, where p, q, r are prime.
So, if a number has 3 factors, its prime factorization has to be p2.
‘abcabc’ = ‘abc’ * 1001 or abc * 7 * 11 * 13
Now, ‘abc’ has to be square of a prime number.
It can be either 121 or 169 (square of either 11 or 13) or it can be the square of some other prime number.
When abc = 121 or 169, then
‘abcabc’ is of the form p3q1r1 1, which should have 4 * 2 * 2 = 16 factors.
When ‘abc’ = square of any other prime number (say 172 which is 289) ,
then ‘abcabc’ is of the form p1q1r1s2 , which should have 2 * 2 * 2 * 3 = 24 factors
So, ‘abcabc’ will have either 16 factors or 24 factors.
Example 4: A number N2 has 15 factors. How many factors can N have?
a. 5 or 7 factors
b. 6 or 8 factors
c. 4 or 6 factors
d. 9 or 8 factors
Ans: Option 'b' is correct.
Sol: Any number of the form paqbrc will have (a + 1) (b + 1) (c + 1) factors, where p, q, r are prime. (This is a very important idea)
N2 has 15 factors.
Now, 15 can be written as 1 x 15 or 3 x 5.
If we take the underlying prime factorization of N2 to be paqb,
then it should have (a + 1) (b + 1) factors.
So, N can be of the form
p14 or p2q4
p14 will have (14 + 1) = 15 factors
p2q4 will have (2 + 1) x (4 + 1) = 15 factors.
Importantly, these are the only two possible prime factorizations that can result in a number having 15 factors.
Hence the answer is 6 or 8 factors.
Example 5: How many three-digit numbers are divisible by 5 or 9?
a) 260
b) 280
c) 200
d) 180
Ans: Option 'a' is correct
Sol: Three digit numbers divisible by 5 or 9 = three digit numbers divisible by 5 + three digit numbers divisible by 9 – three digit numbers divisible by 5 and 9.
The three digit numbers divisible by 5 = 100, 105, 110….995
The sequence given is in A.P with common difference 5. Let 995 be the nth term of the A.P, then, 995 = 100 + (n – 1)5 = 100 + 5n – 5
Thus, n = 180 – (1)
The three digit numbers divisible by 9 = 108, 118, … 999
The sequence given is in A.P with common difference 9. Let 999 be the pth term of the A.P, then, 999 = 108 + (p – 1)9 = 108 + 9p – 9
Thus, p = 100 – (2)
The three digit numbers divisible by 45 = 135, 180, …990
The sequence given is in A.P with common difference 45. Let 990 be the qth term of the A.P, then
990 = 135 + (q – 1)45 = 135 + 45q – 45
Thus, q = 20 – (3)
Thus, from (1), (2) and (3) the three digit numbers divisible by 5 or 9 = 180 + 100 – 20 = 260 so, 260 three- digit numbers are divisible by 5 or 9.
Example 6: If 8A5146B is divisible by 88, then what is the value of AxB?
a) 4
b) 16
c) 8
d) 12
e)18
Ans: Option 'd' is correct
Sol: Since the given number is divisible by 8, the last three digits should also be divisible by 8. Only when B = 4, 46B is a multiple of 8. Thus, B = 4.
As the given number is divisible by 11, the difference between the sum of its odd digits and even digits must be a multiple of 11.
Thus, (8 + 5 + 4 + 4) – (A + 1 + 6) = 14 – A should be divisible by 11. Only when A = 3, 14-A is divisible by 11.
Thus, the value of AxB = 4×3 = 12.
Example 7: What is the number of even factors of 36000 which are divisible by 9 but not by 36?
a) 20
b) 4
c) 10
d) 12
Ans: Option 'b' is correct
Sol: 36000 = 25 * 32 * 53
Since we are talking of even factors, there must be at least one 2 in the required factors.
Since the number is divisible by 9, we must have both the threes.
We cannot have more than 1 two as it will make the number divisible by 36.
So we have 1 way of choosing 2, 1 way of choosing 3, 4 ways of choosing 5.
Thus the required number of factors are:
1*1*4 = 4
Example 8: The number A39K2 is completely divisible by both 8 and 11. Here both A and K are single-digit natural numbers. Which is a possible value of A+K?
a) 8
b) 10
c) 12
d) 14
Ans: Option 'b' is correct
Sol: The number is divisible by 11, so the difference between the sum of the digits at the odd places and the digits at the even places is either 0 or a multiple of 11.
Let the difference be a 0, so
11 + A = 3 + K
=> K – A = 8, the only possible value is 9,1.
Now we have to check if it satisfies the divisibility by 8 test.
K= 9 makes the last 3 digits 992. This is divisible by 8.
Let’s check for other cases when the difference is 11
11 + A – 3 – K = 11 => A – K = 3
The possible values in this case are (9,6), ( 8,5), (7,4), (6,3), (5,2), (4,1).
Among these cases, only (8,5) and (4,1) will be divisible by 8. So the possible values of the sum are 13, 5, and 10.
Now, the difference between the sum of odd and even places cannot be 22
11 + A – 3 – K = 22 => A – K = 14
Since, both A and K are single-digit natural numbers, this is not possible.
Thus the only possible values of sum are 5, 10, and 13.
In the given options only 10 is there. So it is the correct answer.
|
167 videos|229 docs|95 tests
|
FAQs on Important Formulas: Divisibility & Remainder - Quantitative Aptitude (Quant) - CAT
| 1. What are the basic divisibility rules for numbers? |  |
| 2. How do you find the greatest common divisor (GCD) of two numbers? |  |
| 3. What is the difference between GCD and LCM? |  |
| 4. What is modular arithmetic and how is it used in solving problems? |  |
| 5. How can I apply divisibility rules to solve CAT exam problems efficiently? |  |















