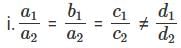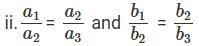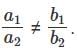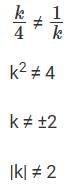Solved Examples: Linear Equations | Quantitative Aptitude (Quant) - CAT PDF Download
Q1: x + |y| = 8, |x| + y = 6. How many pairs of x, y satisfy these two equations?
A: 2
B: 4
C: 0
D: 1
Ans: D
Sol:
We start with the knowledge that the modulus of a number can never be negative, though the number itself may be negative.
The first equation is a pair of lines defined by the equations
y = 8 – x ------- (i) (when y is positive)
y = x – 8 ------- (ii) (when y is negative)
With the condition that x ≤ 8 (because if x becomes more than 8, |y| will be forced to be negative, which is not allowed)
The second equation is a pair of lines defined by the equations:
y = 6 – x ------- (iii) (when x is positive)
y = 6 + x ------- (iv) (when x is negative)
with the condition that y cannot be greater than 6, because if y > 6, |x| will have to be negative.
On checking for the slopes, you will see that lines (i) and (iii) are parallel. Also (ii) and (iv) are parallel (same slope).
Lines (i) and (iv) will intersect, but only for x = 1; which is not possible as equation (iv) holds good only when x is negative.
Lines (ii) and (iii) do intersect within the given constraints. We get x = 7, y = -1. This satisfies both equations.
Only one solution is possible for this system of equations.
Q2: Consider three numbers a, b and c. Max (a,b,c) + Min (a,b,c) = 13. Median (a,b,c) - Mean (a,b,c) = 2. Find the median of a, b, and c.?
A: 11.5
B: 9
C: 9.5
D: 12
Ans: C
Sol:
The numbers can be arranged in ascending order thus:
Min < Median < Max
According to the question,
Min + Max = 13Median = (Min + Med + Max)/3 = Median - (12+ Med)/3 = 2
Solving, we get Median = 9.5
Q3: a1x + b1y + c1z = d1, a2x + b2y + c2z = d2, a3x + b3y + c3z = d3.
Which of the following statements if true would imply that the above system of equations does not have a unique solution?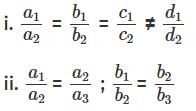
iii. a1, a2, a3 are integers; b1, b2, b3 are rational numbers, c1, c2, c3 are irrational numbers
A: Statement i
B: Statement ii
C: Statement iii
D: None
Ans: A
Sol:
If we have three independent equations, we will have a unique solution. In other words, we will not have unique solutions if:
The equations are inconsistent or
Two equations can be combined to give the third
Now, let us move to the statements.
This tells us that the first two equations cannot hold good at the same time.
Think about this:
x + y + z = 3;
2x + 2y + 2z = 5.
Either the first or the second can hold good. Both cannot hold good at the same time. So, this will definitely not have any solution.
a1, a2, a3 are in GP, b1, b2, b3. This does not prevent the system from having a unique solution.
For instance, if we have
x + 9y + 5z = 11
2x + 3y – 6z = 17
4x + y – 3z = 15
This could very well have a unique solution.
iii. a1, a2, a3 are integers; b1, b2, b3 are rational numbers, c1, c2, c3 are irrational numbers
This gives us practically nothing. This system of equations can definitely have a unique solution.
So, only Statement I tells us that a unique solution is impossible.
Q4: Let k be a constant. The equations kx + y = 3 and 4x + ky = 4 have a unique solution if and only if
A: |k| = 2
B: k ≠ 2
C: |k| ≠ 2
D: k = 2
Ans: C
Sol:
Two generic equations, a1x + b1y + c1 = 0 and a2x + b2y + c2 = 0, will have a unique solution if and only if,
We have the equations kx + y = 3 and 4x + ky = 4,
For them to have unique solutions, they must satisfy the condition
Q5: Aron bought some pencils and sharpeners. Spending the same amount of money as Aron, Aditya bought twice as many pencils and 10 less sharpeners. If the cost of one sharpener is 2 more than the cost of a pencil, then the minimum possible number of pencils bought by Aron and Aditya together is
A: 33
B: 27
C: 30
D: 36
Ans: A
Sol:
(Aron) Px + sx + 2s = (Aditya) 2px + sx – 20 – 10x + 2s
Px = 10x + 20
x(p-10) = 20
Together they bought 3p pencils
Minimum value of p has to be 11
So, minimum pencils they bought together is 33
Q6: In CAT 2007 there were 75 questions. Each correct answer was rewarded by 4 marks and each wrong answer was penalized by 1 mark. In how many different combination of correct and wrong answer is a score of 50 possible?
A: 14
B: 15
C: 16
D: None of these
Ans: D
Sol:
Correct (c) + Wrong (w) + Not attempted (n) = 75
4c – w + 0n = 50
Adding the two equations we get
5c + n = 125
Values of both c & n will be whole numbers in the range [0, 50]
c (max) = 25; when n = 0
c (min) = 13; when n = 60 {Smallest value of ‘c’ which will take the marks from correct questions greater than or equal to 50}
No. of valid combinations will be for all value of ‘c’ from 13 to 25 = 13.
Q7: How many integer solutions exist for the equation 8x – 5y = 221 such that x × y < 0
A: 4
B: 5
C: 6
D: 8
Ans: C
Sol:
We first need to find out a solution for x & y. Once we get a solution, values of x would be in an AP with a common difference of 5 whereas values of y would be in an AP with a common difference of 8.
Valid Solutions:
x = 32; y = 7
x = 37; y = 15
x = 42; y = 23
But we need the solutions where one variable is negative whereas the other one is positive. so, we will move in the other direction.
x = 27; y = -1
x = 22; y = -9
x = 17; y = -17
x = 12; y = -25
x = 7; y = -33
x = 2; y = -41
So, number of integer solutions where x × y < 0 is 6.
Q8: For how many positive integral values of N, less than 40 does the equation 3a – Nb = 5, have no integer solution
A: 13
B: 14
C: 15
D: 12
Ans: A
Sol:
If N is a multiple of 3, then the LHS would be divisible by 3 and RHS won’t be. Number of positive integral values less than 40 which are multiple of 3 = 13.
Q9: The cost of 3 hamburgers, 5 milk shakes, and 1 order of fries at a certain fast food restaurant is $23.50. At the same restaurant, the cost of 5 hamburgers, 9 milk shakes, and 1 order of fries is $39.50. What is the cost of 2 hamburgers, 2 milk shakes, and 2 orders of fries at this restaurant?
A: 10
B: 15
C: 7.5
D: Cannot be determined
Ans: B
Sol:
3H + 5M + 1F = 23.50
5H + 9M + 1F = 39.50
2H + 2M + 2F = ?
Calculate 2(Equation 1) – (Equation 2)
H + M + F = 2×23.5 – 39.5
H + M + F = 7.5
2H + 2M + 2F = 15.
Q10: Two sides of a triangle have lengths 10 and 20. How many integers can take the value of the third side length:
A: 18
B: 19
C: 20
D: 21
Ans: B
Sol:
Let the third side be x
20 – 10 < x < 10 + 20
10 < x < 30
No. of integral values of x = 19.
|
166 videos|231 docs|95 tests
|
FAQs on Solved Examples: Linear Equations - Quantitative Aptitude (Quant) - CAT
| 1. What are linear equations and how are they represented? |  |
| 2. How do you solve a linear equation step by step? |  |
| 3. What are some common applications of linear equations? |  |
| 4. Can linear equations have more than one variable? |  |
| 5. What are the different methods to graph linear equations? |  |