Combining Random Variables Chapter Notes | AP Statistics - Grade 9 PDF Download
It's very useful to transform a random variable by adding or subtracting a constant or multiplying or dividing by a constant. This can help to simplify calculations or to make the results easier to interpret.
Transform
This section is about transforming random variables by adding/subtracting or multiplying/dividing by a constant. At the end of this section, you'll know how to combine random variables to calculate and interpret the mean and standard deviation.
Linear Transformations of a Random Variable
When you transform a random variable by adding or subtracting a constant, the mean and standard deviation of the transformed variable are also shifted by the same constant. For example, if you have a random variable, X, with mean E(X) and standard deviation SD(X), and you transform it to a new random variable, Y, by adding a constant, c, to each value of X, then the mean and standard deviation of Y are given by:
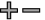
- E(Y) = E(X) + c
- SD(Y) = SD(X)
Similarly, if you transform a random variable by multiplying or dividing it by a constant, the mean and standard deviation of the transformed variable are also multiplied or divided by the same constant. For example: 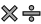
- E(Y) = E(X) * c
- SD(Y) = SD(X) * c
Y = a + BX
When you transform a random variable by adding or subtracting a constant, it affects the measures of center and location, but it does not affect the variability or the shape of the distribution.
When you transform a random variable by multiplying or dividing it by a constant, it affects the measures of center, location, and variability, but it does not change the shape of the distribution.
Expected Value of the Sum/Difference of Two Random Variables
It is also possible to combine two or more random variables to create a new random variable. To calculate the mean and standard deviation of the combined random variable, you would need to use the formulas for the expected value and standard deviation of a linear combination of random variables.
For example, if you have two random variables, X and Y, with means E(X) and E(Y) and standard deviations SD(X) and SD(Y), respectively, and you want to create a new random variable, Z, by adding them together, then the mean of Z is given by:
- E(Z) = E(X) + E(Y)
Summary
- Sum: For any two random variables X and Y, if S = X + Y, the mean of S is mean S = mean X + mean Y. Put simply, the mean of the sum of two random variables is equal to the sum of their means.
- Difference: For any two random variables X and Y, if D = X - Y, the mean of D is mean D = mean X - mean Y. The mean of the difference of two random variables is equal to the difference of their means. The order of subtraction is important.
- Independent Random Variables: If knowing the value of X does not help us predict the value of Y, then X and Y are independent random variables.
Standard Deviation of the Sum/Difference of Two Random Variables
If you have two random variables, X and Y, with means E(X) and E(Y) and standard deviations SD(X) and SD(Y), respectively, and you want to create a new random variable, Z, by adding them together, then the standard deviation of Z is given by:
- SD(Z) = √(SD(X)² + SD(Y)²)
Summary
- Sum: For any two independent random variables X and Y, if S = X + Y, the variance of S is SD² = SDX² + SDY². To find the standard deviation, take the square root: SD = √(SDX² + SDY²). Standard deviations do not add; use the formula or your calculator.
- Difference: For any two independent random variables X and Y, if D = X - Y, the variance of D is D² = SDX² + SDY². To find the standard deviation, take the square root: SD = √(SDX² + SDY²). Notice that you are NOT subtracting the variances.
Practice Problem
Try this one on your own!
Two random variables, X and Y, represent the number of hours a student spends studying for a math test and the number of hours a student spends studying for a science test, respectively. The probability distributions of X and Y are shown in the tables below:


A new random variable, Z, represents the total number of hours a student spends studying for both tests.
- (a) Calculate the mean or expected value of Z.
- (b) Calculate the standard deviation of Z.
- (d) Interpret the results in the context of the problem.
Key Terms to Review
- Independent Random Variables: Independent random variables are two or more variables that do not influence each other's outcomes. Understanding independence is crucial when combining random variables, as it directly affects the way we calculate their means and standard deviations, ensuring accurate statistical analysis.
- Linear Transformations of a Random Variable: A linear transformation of a random variable involves adjusting the variable using a linear equation, typically of the form Y = a + bX. This transformation affects both the mean and standard deviation of the original variable.
- Mean: The mean is a measure of central tendency that represents the average value of a set of numbers.
- Random Variable: A random variable is a numerical outcome of a random process, classified into discrete and continuous types.
- Standard Deviation: Standard deviation measures the amount of variation or dispersion in a set of values.
- Variance: Variance quantifies how much individual data points differ from the mean of the dataset.
|
12 videos|106 docs|12 tests
|
FAQs on Combining Random Variables Chapter Notes - AP Statistics - Grade 9
| 1. What are linear transformations in the context of random variables? |  |
| 2. How do linear transformations affect the mean and variance of a random variable? |  |
| 3. What happens to the distribution of a random variable when it undergoes a linear transformation? |  |
| 4. How can I combine two random variables using linear transformations? |  |
| 5. What is the significance of the linear transformation in real-world applications? |  |















