Grade 9 Exam > Grade 9 Notes > AP Statistics > Chapter Notes: Parameters for a Binomial Distribution
Parameters for a Binomial Distribution Chapter Notes | AP Statistics - Grade 9 PDF Download
In order to use the binomial distribution to model a random event, the event must meet the following four conditions:
- Binary: The possible outcomes of each trial can be classified as a success or a failure.
- Independent: Trials must be independent. Knowing the outcome of one trial must not inform the outcome of any other trial.
- Fixed number: The number of trials n must be fixed in advance.
- Same probability: There must be the same probability of success p on each trial.
(A mnemonic device that might help is BINS: binary, independent, number, same probability!)
If any of these conditions is not met, then the event cannot be modeled using the binomial distribution. For example, if you want to model the number of heads in 10 flips of a biased coin with varying probabilities of heads, then the event cannot be modeled using the binomial distribution.
Describing Mean and Standard Deviation of Binomial Variables
Before proceeding, it's important to note that these formulae only apply in binomial settings, where the conditions for the binomial distribution are met.

- Mean: The mean (expected value) of a binomial random variable X, representing the number of successes in n independent trials with probability of success p, is given by: mean = E(X) = n * p
- Standard deviation: The standard deviation of a binomial random variable X is given by: standard deviation = σX = sqrt(n * p * (1 - p))
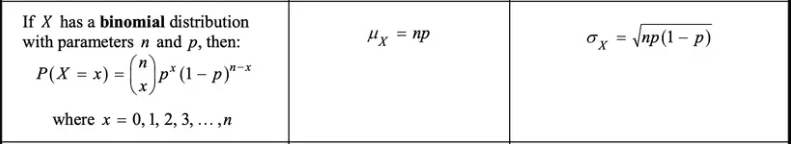
Binomial Distributions in Statistical Sampling
Another important rule is the 10% condition, which states that if you are taking a random sample of size n from a population of size N, and n is less than 10% of N (i.e., n</>N), then you can use a binomial model to describe the number of successes in the sample.
This rule is based on the assumption that the sample is representative of the population, and the probability of success is the same in the sample as it is in the population. If these assumptions are not met, the binomial model may not be appropriate.
Question for Chapter Notes: Parameters for a Binomial DistributionTry yourself: What is one of the conditions for using the binomial distribution?View Solution
Key Terms to Review
- 10% Condition: A guideline ensuring that the sample size taken from a population is small enough relative to the population size, typically indicating that the sample size should be less than 10% of the total population.
- Binomial Distribution: A probability distribution summarizing the likelihood of a given number of successes in a fixed number of independent Bernoulli trials.
- Expected Value: Represents the average outcome of a random variable based on its possible values, weighted by the likelihood of occurrence.
- Failure: The outcome that is not classified as a success in a binomial distribution.
- Mean: A measure of central tendency that represents the average value of a set of numbers.
- Probability of Success: The likelihood that a given outcome will occur in a statistical experiment.
- Random Variable: A numerical outcome of a random process, classified into discrete and continuous types.
- Random Sample: A subset of individuals chosen from a larger population where each individual has an equal chance of being selected.
- Standard Deviation: A measure of the amount of variation or dispersion in a set of values.
The document Parameters for a Binomial Distribution Chapter Notes | AP Statistics - Grade 9 is a part of the Grade 9 Course AP Statistics.
All you need of Grade 9 at this link: Grade 9
|
12 videos|106 docs|12 tests
|
FAQs on Parameters for a Binomial Distribution Chapter Notes - AP Statistics - Grade 9
| 1. What are the key parameters of a binomial distribution? |  |
Ans. The key parameters of a binomial distribution are n and p. Here, n represents the number of trials, and p represents the probability of success on each trial. The binomial distribution models the number of successes in n independent Bernoulli trials.
| 2. How do you calculate the mean of a binomial distribution? |  |
Ans. The mean of a binomial distribution can be calculated using the formula: mean = n * p, where n is the total number of trials and p is the probability of success on each trial.
| 3. What is the formula for the variance of a binomial distribution? |  |
Ans. The variance of a binomial distribution is calculated using the formula: variance = n * p * (1 - p). This formula takes into account the number of trials (n), the probability of success (p), and the probability of failure (1 - p).
| 4. Can you explain what a Bernoulli trial is in the context of a binomial distribution? |  |
Ans. A Bernoulli trial is a random experiment that results in a binary outcome – typically labeled as "success" or "failure." In the context of a binomial distribution, a series of Bernoulli trials are performed, and the binomial distribution describes the number of successes in these trials.
| 5. How do you determine if a situation can be modeled by a binomial distribution? |  |
Ans. A situation can be modeled by a binomial distribution if it meets the following criteria: there are a fixed number of trials (n), each trial has two possible outcomes (success or failure), the trials are independent, and the probability of success (p) remains constant for each trial.
Related Searches















