Overview: Means Chapter Notes | AP Statistics - Grade 9 PDF Download
| Table of contents |

|
| Inference for Quantitative Data |

|
| Confidence Intervals |

|
| Significance Tests |

|
| Two-Sample Inference |

|
In this unit, students will analyze quantitative data to make inferences about population means. Students should understand that t and t-tests are used for inference with means when the population standard deviation, σ, is not known. Using s for σ in the formula for z gives a slightly different value, t, whose distribution, which depends on sample size, has more area in the tails than a normal distribution. The boundaries for rejecting a null hypothesis using a t-distribution tend to be further from the mean than for a normal distribution. Students should understand how and why conditions for inference with proportions and means are similar and different.
Inference for Quantitative Data
Have you ever been given a piece of information and said, "Wait, that just doesn't sound right!"
In this unit, we are going to tackle how we can actually test these claims when dealing with quantitative data. We are going to see how we can estimate the true mean of a population or test a given claim about a population.
Similar to the previous unit, there are several ways to test claims about a population when dealing with quantitative data. One common method is to use hypothesis testing, which involves stating a null hypothesis and an alternate hypothesis, and then using statistical analysis to determine which hypothesis is more supported by the data.
Another method is to use confidence intervals, which provide a range of values within which the true population mean is likely to fall. A confidence interval can be calculated based on a sample mean and a measure of the sample's dispersion, such as the standard deviation. The larger the sample size and the smaller the standard deviation, the narrower the confidence interval will be.
Confidence Intervals
The first half of this unit is dedicated to constructing and interpreting confidence intervals. A confidence interval is a range of numbers with which we can estimate, or predict, a true population mean or proportion.
In order to construct a confidence interval, we need to make sure that three conditions are met, which are similar to the conditions in Unit 6.
Random
The first thing that is essential to constructing a confidence interval is to make sure that our sample statistic is taken from a random sample. If our sample statistic is obtained from a random sample from our population, it is known as an unbiased estimator, which is exactly what we want to get a good estimate.
Independence
The next thing we need to check is that our sample is taken independently. As you recall from Unit 6, most of the time our samples are taken without replacement, so therefore they technically are not independent. Therefore, we can check the 10% condition, which states that the population is at least 10x the sample size. This is a necessary piece of calculating a confidence interval because it allows us to use the standard deviation formula given on our formula sheet.
Normal
The normal distribution is a tad different for quantitative data (means). Rather than using a z* as our critical value, we will shift to using the family of t distributions, which is based on the sample size. We will discuss that more later in the coming sections. For now, in order to be able to use the t distribution, you will need to be sure that one of the three things is true:
- The population is normally distributed.
- The sample size is at least 30. This is known as the Central Limit Theorem. Some people refer to this as the Fundamental Theorem of Statistics since so much of our calculations hinge on this fact being true.
- If worse comes to worse and our sample size isn't large enough, we can also check that a sampling distribution for our sample mean is approximately normal by plotting our random sample on a box-plot or dot-plot and showing that it has no skewness or outliers.
Significance Tests
The second half of this unit is dedicated to significance tests. This is when we have a claim from the author regarding the true population mean, but we also have a sample mean and standard deviation that leads us to doubt this claim.
Conditions
The same conditions that we checked above for confidence intervals also need to hold in order to perform a significance test. We need to make sure our sample is random, the 10% condition is met, and the sampling distribution for our sample mean is approximately normal.
In order to test a given claim, we will calculate the probability of obtaining our sample mean assuming that the author's population claim is true. Therefore, we will create a sampling distribution based off of the information given by the author and see where our sample mean would fit in. If our sample mean lies far in one of the two tails, that gives us reason to doubt that their claim is actually true since our sample was randomly selected from this population and assuming our normal condition is met.
Example
For example, the local Co-Op says that they get in approximately 25 every Thursday. You have been checking their inventory for 35 days and have found the average number of to be only 21. Is the Co-Op not being truthful or are your different findings due to simply sampling variability? We will return to this claim later in this unit and actually perform a test.
Two-Sample Inference
Another essential part of inference with quantitative data involves constructing a confidence interval or running a significance test for the difference in two sample means. This comes in handy a lot in experimental design as we are testing the differences in means between two treatment groups, or trying to find the average difference between the two groups.
For instance, if we were comparing two treatments for poison ivy, we may randomly assign one group of patients one cream and the second group a different cream and compare the average number of days it took for symptoms to subside. We could analyze the effectiveness using both a confidence interval or a significance test.
Other questions that this unit will tackle include:
- How do we know whether to use a t-test or a z-test for inference with means?
The t-test and the z-test are both used for inference with means, but they are used in different situations. The t-test is used when the population standard deviation is unknown and the sample size is small (usually n < 30).
The z-test is used when the population standard deviation is known and the sample size is large (usually n ≥ 30). It is also used when the sample is drawn from a normally distributed population. The z-test assumes that the population standard deviation is known, so it does not take into account the variability in the sample to the same extent as the t-test.
- How can we make sure that samples are independent?
- Why is it inappropriate to accept a hypothesis as true based on the results of statistical inference testing?
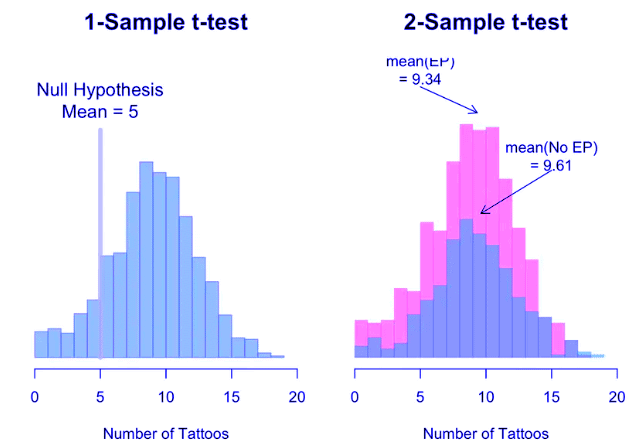
Key Terms to Review
- 10% Condition: The 10% Condition is a guideline used in statistics to ensure that the sample size taken from a population is small enough relative to the population size, typically indicating that the sample size should be less than 10% of the total population.
- Box Plot: A graphical representation of a dataset summarizing its key statistics, including the median, quartiles, and potential outliers.
- Central Limit Theorem: States that the sampling distribution of the sample mean approaches a normal distribution as the sample size increases, regardless of the population's distribution.
- Confidence Interval: A range of values derived from sample statistics that is likely to contain the true value of an unknown population parameter, with a specified level of confidence.
- Dot Plot: A graphical display used to represent the frequency of individual data points in a dataset.
- Experimental Design: The process of planning an experiment to ensure that it can adequately address the research question being investigated.
- Independence: Refers to the statistical concept where the occurrence or outcome of one event does not affect the occurrence or outcome of another event.
- Normal Distribution: A continuous probability distribution characterized by a symmetric, bell-shaped curve.
- Null Hypothesis: A statement that assumes there is no effect or no difference in a given situation, serving as the foundation for statistical testing.
- Outliers: Data points that significantly differ from the rest of the data in a dataset.
- Quantitative Data: Numerical information that can be measured or counted, allowing for statistical analysis.
- Random Sample: A subset of individuals chosen from a larger population, where each individual has an equal chance of being selected.
- Sample Variability: The natural differences that occur between the results obtained from different samples taken from the same population.
- Sampling Distribution: A probability distribution of a statistic obtained by selecting random samples from a population.
- Significance Tests: Statistical methods used to determine whether the observed data significantly deviates from what would be expected under a specific hypothesis.
- Skewness: Measures the asymmetry of a probability distribution.
- T-tests: A statistical method used to determine if there is a significant difference between the means of two groups.
- T-Distribution: A type of probability distribution used primarily in hypothesis testing and constructing confidence intervals when the sample size is small.
- T-test: A statistical test used to determine if there is a significant difference between the means of two groups.
- Treatment Groups: Specific groups of subjects that receive different levels or types of treatment in an experiment.
- Two-Sample Inference: Statistical methods used to compare the means or proportions from two independent samples.
- Unbiased Estimator: A statistical estimator that, on average, hits the true parameter of the population being estimated.
- Z-test: A statistical method used to determine if there is a significant difference between the means of two groups.
- Z: Represents a standard score or z-score, indicating how many standard deviations an element is from the mean of a distribution.
|
12 videos|106 docs|12 tests
|
FAQs on Overview: Means Chapter Notes - AP Statistics - Grade 9
| 1. What is the purpose of constructing a confidence interval in statistics? |  |
| 2. What conditions must be met to construct a confidence interval? |  |
| 3. When should a t-test be used instead of a z-test? |  |
| 4. how do we determine if samples are independent in a statistical study? |  |
| 5. what is the significance of the null hypothesis in hypothesis testing? |  |
| 4.="" how="" do="" we="" determine="" if="" samples="" are="" independent="" in="" a="" statistical="" study?="" |  |
| 5.="" what="" is="" the="" significance="" of="" the="" null="" hypothesis="" in="" hypothesis="" testing?="" |  |
| 4. how do we determine if samples are independent in a statistical study? |  |
| 5. what is the significance of the null hypothesis in hypothesis testing? |  |














