Integrating Vector-Valued Functions Chapter Notes | Calculus BC - Grade 9 PDF Download

Document Description: Chapter Notes: Integrating Vector-Valued Functions for Grade 9 2025 is part of Calculus BC preparation. The notes and questions for Chapter Notes: Integrating Vector-Valued Functions have been prepared according to the Grade 9 exam syllabus. Information about Chapter Notes: Integrating Vector-Valued Functions covers topics like 9.5 Integrating Vector-Valued Functions, 🔭 Integrating Vector-Valued FunctionsIt’s good to first recognize the format of your function. 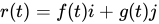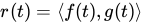It is either written in two or three dimensions; we want to know which one so that we are not confused about which terms should be paid attention to when integrating.A two-dimensional vector function might look like this:or like this:These both mean the same thing! 🚀❓ How do we integrate?Luckily, we integrate each component of a vector function separately. No need to make things more complicated than they need to be! You look at each component as if it was its own problem. 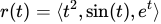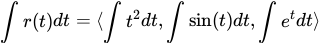Let’s go through an example just to see how the College Board might ask a question like this.✏️ Integrating Vector-Valued Functions WalkthroughWe are given:We know we are going to need to integrate this vector-valued function, so let’s re-write this including integrals on each component.You can solve each of these integrals separately. If you need help with integrals, check out our guide 6.14 Selecting Techniques for Antidifferentiation. 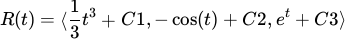Although it says for AB, it will apply to this!6.14 Selecting Techniques for AntidifferentiationOur final answer will be:Please note that C1, C2, and C3 just represent different possible constants and I added them for clarity. For these types of problems, you will typically get definite integrals so that there is less ambiguity. Follow your typical steps for solving these problems!📝 Additional Practice ProblemLet’s try a word problem now (note this is a calculator-okay question). This problem (#9) is from the flipped math calculus website. 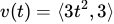All credit to them.(note this is a calculator-okay question).flipped math calculus websiteAt time \( t \geq 0 \), a particle moving in the \( xy \)-plane has a velocity vector given by:If the particle is at point (1,2) at time \( t = 0 \), how far is the particle from the origin at time \( t = 2 \?Try the problem on your own first! If you are stuck, read through our explanation below!🏆 Solution to Practice ProblemStep one is integrating the function. As we’ve discussed, you will integrate each of the components of the vector function separately. 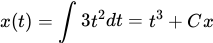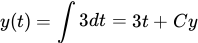Before applying conditions, this is what you should have for your integrated vector function:The \( C_x \) and \( C_y \) constants are just placeholders. 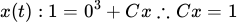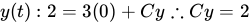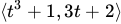We are going to figure out those numbers now:Since we are given the position for \( t=0 \), we can use that information to work backward and find our constants.Now that we know the values for our constants, let's put those into our integrated vector functions:Now we’re done with the hard parts! From here on it’s just simple math to finish off the problem. We will plug in \( t=2 \) to our equation to find the position of the particle at that point. 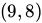This gives us:Finally, we’ll use the handy distance formula to find how far this point is from the origin. 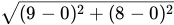Since this would be a question in the calculator section, you’ll want to plug this into your calculator and give a number rounded to three decimal places rather than leave it in radical form.You should get 12.04 units as your final answer!Why integrate vector-valued functions?With these types of problems, you want to have a good understanding of what you can do with the functions. Vector functions often tell you the movement or position of a particle. This means the integrated function can give the total area moved over time or similar. Don’t worry too much about the nitty-gritty, but practice recognizing graphs for regular functions and matching them to their differentiated or integrated functions. You can get practice with this in our guide 9.6! Good luck and you’ve got this. 😁9.6Key Terms to Review (13)Cartesian Coordinates: A system used to locate points on a plane using two perpendicular lines called axes (usually x and y).Change of variables: Refers to substituting one variable with another variable or expression to simplify an integral or equation.Definite Integral: A mathematical tool used to calculate the exact area between a function and the x-axis over a specific interval.Displacement: Refers to the change in position of an object from its initial point to its final point, taking into account both distance and direction.Green's Theorem: Relates a double integral over a region in the plane to a line integral around its boundary.Indefinite Integral: The reverse process of differentiation; represents a family of functions that have the same derivative.Integrals: Mathematical tools used to find the area under a curve or to calculate the accumulation of quantities over a given interval.Integration by Parts: A technique used to find the integral of a product of two functions.Line Integrals: Measures the total effect along a curve or path, considering both direction and magnitude.Polar Coordinates: A coordinate system used to locate points in space using radial distance (r) and angular displacement (θ).Real-valued functions: Functions that take real numbers as inputs and produce real numbers as outputs.Substitution: An integration technique used to simplify complex integrands by replacing variables.Vector-valued functions: Functions that output vectors instead of scalars, taking in a parameter (usually denoted as t). and Chapter Notes: Integrating Vector-Valued Functions Example, for Grade 9 2025 Exam. Find important definitions, questions, notes, meanings, examples, exercises and tests below for Chapter Notes: Integrating Vector-Valued Functions.

Introduction of Chapter Notes: Integrating Vector-Valued Functions in English is available as part of our Calculus BC for Grade 9 & Chapter Notes: Integrating Vector-Valued Functions in Hindi for Calculus BC course. Download more important topics related with notes, lectures and mock test series for Grade 9 Exam by signing up for free. Grade 9: Integrating Vector-Valued Functions Chapter Notes | Calculus BC - Grade 9