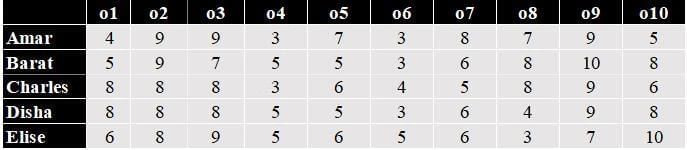
CAT Previous Year Questions: Generic Puzzles | Logical Reasoning (LR) and Data Interpretation (DI) PDF Download
2024
Passage - 1
Direction: Answer the following questions based on the information given below.
Two students, Amiya and Ramya are the only candidates in an election for the position of class representative. Students will vote based on the intensity level of Amiya’s and Ramya’s campaigns and the type of campaigns they run. Each campaign is said to have a level of 1 if it is a staid campaign and a level of 2 if it is a vigorous campaign. Campaigns can be of two types, they can either focus on issues, or on attacking the other candidate.
If Amiya and Ramya both run campaigns focusing on issues, then
- The percentage of students voting in the election will be 20 times the sum of the levels of campaigning of the two students. For example, if Amiya and Ramya both run vigorous campaigns, then 20 × (2+2)%, that is, 80% of the students will vote in the election.
- Among voting students, the percentage of votes for each candidate will be proportional to the levels of their campaigns. For example, if Amiya runs a staid (i.e., level 1) campaign while Ramya runs a vigorous (i.e., level 2) campaign, then Amiya will receive 1/3 of the votes cast, and Ramya will receive the other 2/3. The above-mentioned percentages change as follows if at least one of them runs a campaign attacking their opponent.
- If Amiya runs a campaign attacking Ramya and Ramya runs a campaign focusing on issues, then 10% of the students who would have otherwise voted for Amiya will vote for Ramya, and another 10% who would have otherwise voted for Amiya, will not vote at all.
- If Ramya runs a campaign attacking Amiya and Amiya runs a campaign focusing on issues, then 20% of the students who would have otherwise voted for Ramya will vote for Amiya, and another 5% who would have otherwise voted for Ramya, will not vote at all.
- If both run campaigns attacking each other, then 10% of the students who would have otherwise voted for them had they run campaigns focusing on issues, will not vote at all.
Q1: If both of them run staid campaigns attacking the other, then what percentage of students will vote in the election?
A: 60%
B: 36%
C: 64%
D: 40%
Ans: B
Sol: If both of them run staid campaigns means (1+1), and normally there will be a voting percentage of 20(1+1)% = 40%. But since they are attacking one other, then 10% of the 40% of voters will not vote at all. So, the percentage of students who will vote in the election is = 90% of 40% = 36%
So, 36% of the students will vote in the election.
Q2: What is the minimum percentage of students who will vote in the election?
A: 40%
B: 32%
C: 38%
D: 36%
Ans: D
Sol: The minimum percentage of students will vote in the election if both Ramya and Amiya run staid campaigns attacking each other. In this case, if both of them run staid campaigns means (1+1), and normally there will be a voting percentage of 20(1+1)% = 40%. But since they are attacking one other, then 10% of the 40% of voters will not vote at all. So, the percentage of students who will vote in the election is = 90% of 40% = 36%
So, a minimum of 36% of the students will vote in the election.
Q3: If Amiya runs a campaign focusing on issues, then what is the maximum percentage of votes that she can get?
A: 48%
B: 40%
C: 44%
D: 36%
Ans: A
Sol: If Amiya runs a campaign focusing on issues, then she will get the maximum percentage of votes if she runs a vigorous campaign and her opponent Ramya runs an attacking campaign vigorously.
In a normal case, there will be a total of 20(2+2) = 80% voters voting 40% each for Amiya and Ramya, but since Ramya is running as an opponent 20% of her voters will vote for Amiya. So, the maximum percentage of votes that Amiya can get = 40% + 20%of40% = 40% + 8% = 48%
Q4: If Ramya runs a campaign attacking Amiya, then what is the minimum percentage of votes that she is guaranteed to get?
A: 12%
B: 18%
C: 15%
D: 30%
Ans: C
Sol: In this case, the minimum percentage of votes she is guaranteed to get when she runs a staid campaign, and Amiya can run either a staid campaign or a vigorous campaign focussing on issues.
The minimum percentage votes of Ramya = 20% - 20%of20% - 5%of20% = 20% - 4% - 1% = 15%
So, a minimum of 15% of votes are guaranteed for Ramya.
Passage - 2
Answer the following questions based on the information given below.
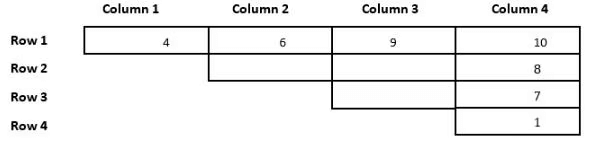
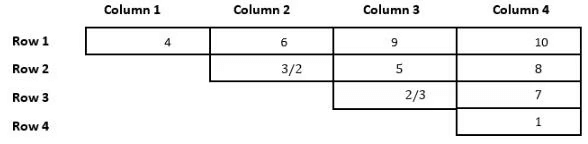
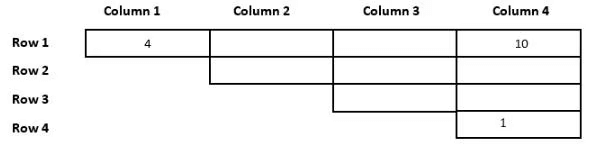
The numbers 1, 2, 3, 4, 5, 6, 7, 8, 9, and 10 are placed in ten slots of the following grid based on the conditions below.
1. Numbers in any row appear in an increasing order from left to right.
2. Numbers in any column appear in a decreasing order from top to bottom.
3. 1 is placed either in the same row or in the same column as 10.
4. Neither 2 nor 3 is placed in the same row or in the same column as 10.
5. Neither 7 nor 8 is placed in the same row or in the same column as 9.
6. 4 and 6 are placed in the same row.
Q1: What is the row number which has the least sum of numbers placed in that row?
Ans: 4
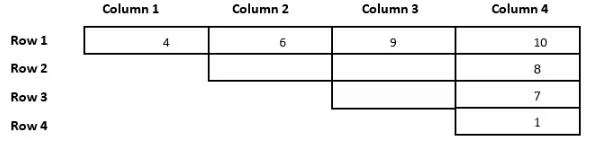
Sol: From point 1 and point 2, we can say that the number 10 can only take the cell R1C4, Similarly the number 9 can only take the place of R1C3 or R2C4. So, the numbers 2 and 3 can only take the places C2R2, C3R2, and C3R3. The numbers 4 and 6 are placed in the same row, they cannot be in row 4 because it has only one cell, and they cannot be in row 3 because then it violates condition 2 as either 2 or 3 will be above 4 which is not possible, they cannot be in row 2, because it violates condition 5 and 4. Hence the only place they can take is in rows 1 and 4, which will take the cell number C1R1 and now 1 comes in the bottom of column 4. With this information, we can make the following table.
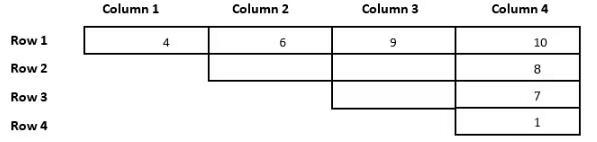
As we can see from the above table, 9 cannot be in the 4th column because it violates condition 5. So, the number 9 will take cell C3R1. Now the numbers 8 and 7 will take the two cells below the number 10 and get the following table.
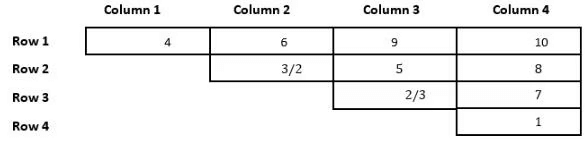
Now, the remaining numbers are 5, 2, and 3. The only place 4 can take is just below 9, and the numbers 2 and 3 can be C2 or C3. Finally, we get the following table.
As we can see from the above table the row with the least sum is row 4, sum = 1
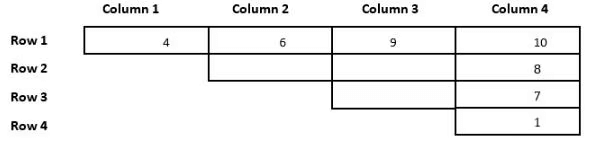
Q2: Which of the following statements MUST be true?
I. 10 is placed in a slot in Row 1.
II. 1 is placed in a slot in Row 4.
(a) Only II
(b) Neither I nor II
(c) Only I
(d) Both I and II
Ans: (d)
Sol: From point 1 and point 2, we can say that the number 10 can only take the cell R1C4, Similarly the number 9 can only take the place of R1C3 or R2C4. So, the numbers 2 and 3 can only take the places C2R2, C3R2, and C3R3. The numbers 4 and 6 are placed in the same row, they cannot be in row 4 because it has only one cell, and they cannot be in row 3 because then it violates condition 2 as either 2 or 3 will be above 4 which is not possible, they cannot be in row 2, because it violates condition 5 and 4. Hence the only place they can take is in rows 1 and 4, which will take the cell number C1R1 and now 1 comes in the bottom of column 4. With this information, we can make the following table.
As we can see from the above table, 9 cannot be in the 4th column because it violates condition 5. So, the number 9 will take cell C3R1. Now the numbers 8 and 7 will take the two cells below the number 10 and get the following table.
Now, the remaining numbers are 5, 2, and 3. The only place 4 can take is just below 9, and the numbers 2 and 3 can be C2 or C3. Finally, we get the following table.
As we can see from the above table both the statements MUST be true.
Q3: Which of the following statements MUST be true?
I. 2 is placed in a slot in Column 2.
II. 3 is placed in a slot in Column 3.
(a) Only II
(b) Neither I nor II
(c) Only I
(d) Both I and II
Ans: (b)
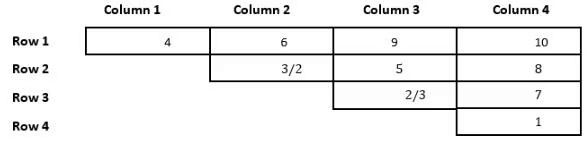
Sol: From point 1 and point 2, we can say that the number 10 can only take the cell R1C4, Similarly the number 9 can only take the place of R1C3 or R2C4. So, the numbers 2 and 3 can only take the places C2R2, C3R2, and C3R3. The numbers 4 and 6 are placed in the same row, they cannot be in row 4 because it has only one cell, and they cannot be in row 3 because then it violates condition 2 as either 2 or 3 will be above 4 which is not possible, they cannot be in row 2, because it violates condition 5 and 4. Hence the only place they can take is in rows 1 and 4, which will take the cell number C1R1 and now 1 comes in the bottom of column 4. With this information, we can make the following table.
As we can see from the above table, 9 cannot be in the 4th column because it violates condition 5. So, the number 9 will take cell C3R1. Now the numbers 8 and 7 will take the two cells below the number 10 and get the following table.
Now, the remaining numbers are 5, 2, and 3. The only place 4 can take is just below 9, and the numbers 2 and 3 can be C2 or C3. Finally, we get the following table.
Both statements can be true, but it is not necessary that both statements must be TRUE. Hence option B is correct.
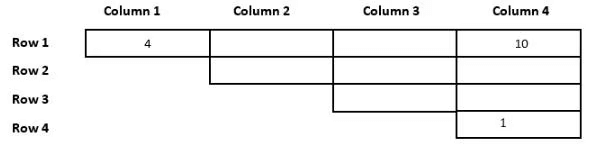
Q4: For how many slots in the grid, placement of numbers CANNOT be determined with certainty?
Ans: 2
Sol: From point 1 and point 2, we can say that the number 10 can only take the cell R1C4, Similarly the number 9 can only take the place of R1C3 or R2C4. So, the numbers 2 and 3 can only take the places C2R2, C3R2, and C3R3. The numbers 4 and 6 are placed in the same row, they cannot be in row 4 because it has only one cell, and they cannot be in row 3 because then it violates condition 2 as either 2 or 3 will be above 4 which is not possible, they cannot be in row 2, because it violates condition 5 and 4. Hence the only place they can take is in rows 1 and 4, which will take the cell number C1R1 and now 1 comes in the bottom of column 4. With this information, we can make the following table.
As we can see from the above table, 9 cannot be in the 4th column because it violates condition 5. So, the number 9 will take cell C3R1. Now the numbers 8 and 7 will take the two cells below the number 10 and get the following table.
Now, the remaining numbers are 5, 2, and 3. The only place 4 can take is just below 9, and the numbers 2 and 3 can be C2 or C3. Finally, we get the following table.
As we can see from the above final table, we cannot determine the unique places of the numbers 2 and 3, Hence the answer is 2.
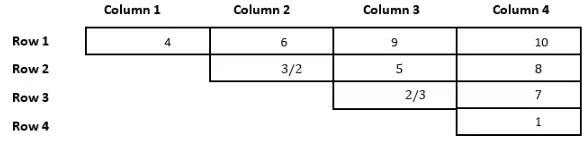
Q5: What is the sum of the numbers placed in Column 4?
Ans: 26
Sol: From point 1 and point 2, we can say that the number 10 can only take the cell R1C4, Similarly the number 9 can only take the place of R1C3 or R2C4. So, the numbers 2 and 3 can only take the places C2R2, C3R2, and C3R3. The numbers 4 and 6 are placed in the same row, they cannot be in row 4 because it has only one cell, and they cannot be in row 3 because then it violates condition 2 as either 2 or 3 will be above 4 which is not possible, they cannot be in row 2, because it violates condition 5 and 4. Hence the only place they can take is in rows 1 and 4, which will take the cell number C1R1 and now 1 comes in the bottom of column 4. With this information, we can make the following table.
As we can see from the above table, 9 cannot be in the 4th column because it violates condition 5. So, the number 9 will take cell C3R1. Now the numbers 8 and 7 will take the two cells below the number 10 and get the following table.
Now, the remaining numbers are 5, 2, and 3. The only place 4 can take is just below 9, and the numbers 2 and 3 can be C2 or C3. Finally, we get the following table.
10+8+7+1 = 26
Passage -3
Answer the following questions based on the information given below.
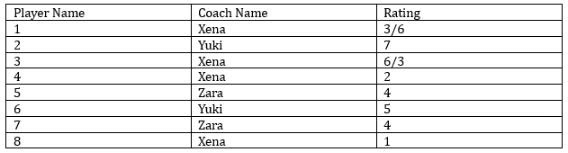
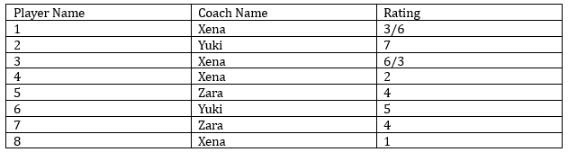
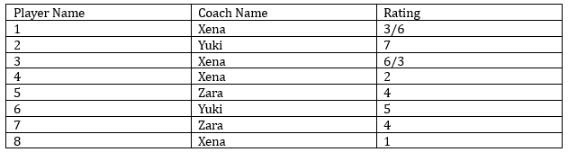
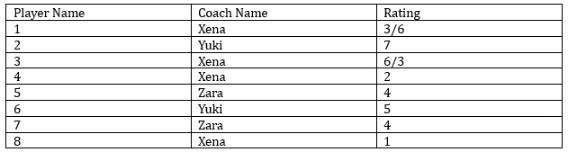
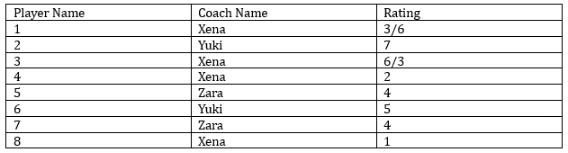
Eight gymnastics players numbered 1 through 8 underwent a training camp where they were coached by three coaches - Xena, Yuki, and Zara. Each coach trained at least two players. Yuki trained only even numbered players, while Zara trained only odd numbered players. After the camp, the coaches evaluated the players and gave integer ratings to the respective players trained by them on a scale of 1 to 7, with 1 being the lowest rating and 7 the highest.
The following additional information is known.
1. Xena trained more players than Yuki.
2. Player-1 and Player-4 were trained by the same coach, while the coaches who trained Player-2, Player-3 and Player-5 were all different.
3. Player-5 and Player-7 were trained by the same coach and got the same rating. All other players got a unique rating.
4. The average of the ratings of all the players was 4.
5. Player-2 got the highest rating.
6. The average of the ratings of the players trained by Yuki was twice that of the players trained by Xena and two more than that of the players trained by Zara.
7. Player-4's rating was double of Player-8's and less than Player-5's.
Q1: What best can be concluded about the number of players coached by Zara?
(a) Either 2 or 3
(b) Exactly 3
(c) Either 2 or 3 or 4
(d) Exactly 2
Ans: (d)
Sol: Let the 8 players be P-1 through P-8, Now it is given that each coach trained at least two players and the number of players coached by Xena is more than Yuki. So the only combination of players trained by the three coaches Xena, Yuki, and Zara must be either 3, 2, and 3 respectively, or 4, 2, and 2 respectively.From statement 2 we can say that P-1 and P-4 were trained by Xena because one is odd and the other is even, and the only coach who can coach both odd and even-numbered is Xena. P-2, P-3, and P-5 were all coached by different coaches. 3 and 5 both are odd so these two players must be coached by Xena and Zara one each in any order. P-2 will be trained by Yuki. Both P-5 and P-7 were trained by the same coach.
With this information, we can get the following table.
From the above table, we can say that the possible players coached by Zara must be 5 and P-7 or only P-3 which is not possible because each coach coached at least two players hence with this we can say that players 5 and 7 were coached by Zara and P-3 was coached by Xena. So, Xena will coach four players and Zara will coach two players.
The average rating of all eight players is 4. So, the total rating is 32. Only P-5 and P-7 got the same rating and all the remaining players got a unique rating. Let the rating got by P-5 and P-7 be x. According to the problem,1+2+3+..+7+n = 32
n = 4
So the rating of P-5 and P-7 is 4 each. P-2 got the highest rating which means he got a rating of 7. P-4’s rating is double that of P-8 but less than P-5, so the rating of P-4 must be 2 and the rating of P-8 must be 1. Because P-4’s rating cannot be 4 and it cannot be 6. With this information, we get the following table.
The only ratings remaining for the players are 3, 5, and 6. It is given that the average ratings given by Yuki is two more than that of Zara. The average rating given by Zara = 4. So, the average rating given by Yuki = is 6. One player got a rating of 7 so the other must get a rating of 5. So, P-6 will be coached by Yuki and get a rating of 5. P-8 will be coached by Xena and P-1 and P-3 will get a rating of 3 and 6 in any order. Finally, we get the following table.
Zara coached exactly two players
Q2: What was the rating of Player-7?
Ans: 4
Sol: Let the 8 players be P-1 through P-8, Now it is given that each coach trained at least two players and the number of players coached by Xena is more than Yuki. So the only combination of players trained by the three coaches Xena, Yuki, and Zara must be either 3, 2, and 3 respectively, or 4, 2, and 2 respectively.
From statement 2 we can say that P-1 and P-4 were trained by Xena because one is odd and the other is even, and the only coach who can coach both odd and even-numbered is Xena. P-2, P-3, and P-5 were all coached by different coaches. 3 and 5 both are odd so these two players must be coached by Xena and Zara one each in any order. P-2 will be trained by Yuki. Both P-5 and P-7 were trained by the same coach.With this information, we can get the following table.
From the above table, we can say that the possible players coached by Zara must be 5 and P-7 or only P-3 which is not possible because each coach coached at least two players hence with this we can say that players 5 and 7 were coached by Zara and P-3 was coached by Xena. So, Xena will coach four players and Zara will coach two players.
The average rating of all eight players is 4. So, the total rating is 32. Only P-5 and P-7 got the same rating and all the remaining players got a unique rating. Let the rating got by P-5 and P-7 be x. According to the problem,1+2+3+..+7+n = 32
n = 4
So the rating of P-5 and P-7 is 4 each. P-2 got the highest rating which means he got a rating of 7. P-4’s rating is double that of P-8 but less than P-5, so the rating of P-4 must be 2 and the rating of P-8 must be 1. Because P-4’s rating cannot be 4 and it cannot be 6. With this information, we get the following table.
The only ratings remaining for the players are 3, 5, and 6. It is given that the average ratings given by Yuki is two more than that of Zara. The average rating given by Zara = 4. So, the average rating given by Yuki = is 6. One player got a rating of 7 so the other must get a rating of 5. So, P-6 will be coached by Yuki and get a rating of 5. P-8 will be coached by Xena and P-1 and P-3 will get a rating of 3 and 6 in any order. Finally, we get the following table.
P-7 got a rating of 4
Q3: What was the rating of Player-6?
Ans: 5
Sol: Let the 8 players be P-1 through P-8, Now it is given that each coach trained at least two players and the number of players coached by Xena is more than Yuki. So the only combination of players trained by the three coaches Xena, Yuki, and Zara must be either 3, 2, and 3 respectively, or 4, 2, and 2 respectively.
From statement 2 we can say that P-1 and P-4 were trained by Xena because one is odd and the other is even, and the only coach who can coach both odd and even-numbered is Xena. P-2, P-3, and P-5 were all coached by different coaches. 3 and 5 both are odd so these two players must be coached by Xena and Zara one each in any order. P-2 will be trained by Yuki. Both P-5 and P-7 were trained by the same coach.
With this information, we can get the following table.
From the above table, we can say that the possible players coached by Zara must be 5 and P-7 or only P-3 which is not possible because each coach coached at least two players hence with this we can say that players 5 and 7 were coached by Zara and P-3 was coached by Xena. So, Xena will coach four players and Zara will coach two players.
The average rating of all eight players is 4. So, the total rating is 32. Only P-5 and P-7 got the same rating and all the remaining players got a unique rating. Let the rating got by P-5 and P-7 be x. According to the problem,1+2+3+..+7+n = 32
n = 4
So the rating of P-5 and P-7 is 4 each. P-2 got the highest rating which means he got a rating of 7. P-4’s rating is double that of P-8 but less than P-5, so the rating of P-4 must be 2 and the rating of P-8 must be 1. Because P-4’s rating cannot be 4 and it cannot be 6. With this information, we get the following table.
The only ratings remaining for the players are 3, 5, and 6. It is given that the average ratings given by Yuki is two more than that of Zara. The average rating given by Zara = 4. So, the average rating given by Yuki = is 6. One player got a rating of 7 so the other must get a rating of 5. So, P-6 will be coached by Yuki and get a rating of 5. P-8 will be coached by Xena and P-1 and P-3 will get a rating of 3 and 6 in any order. Finally, we get the following table.
P-6 got a rating of 5
Q4: For how many players the ratings can be determined with certainty?
Ans: 6
Sol: Let the 8 players be P-1 through P-8, Now it is given that each coach trained at least two players and the number of players coached by Xena is more than Yuki. So the only combination of players trained by the three coaches Xena, Yuki, and Zara must be either 3, 2, and 3 respectively, or 4, 2, and 2 respectively.From statement 2 we can say that P-1 and P-4 were trained by Xena because one is odd and the other is even, and the only coach who can coach both odd and even-numbered is Xena. P-2, P-3, and P-5 were all coached by different coaches. 3 and 5 both are odd so these two players must be coached by Xena and Zara one each in any order. P-2 will be trained by Yuki. Both P-5 and P-7 were trained by the same coach.
With this information, we can get the following table.
From the above table, we can say that the possible players coached by Zara must be 5 and P-7 or only P-3 which is not possible because each coach coached at least two players hence with this we can say that players 5 and 7 were coached by Zara and P-3 was coached by Xena. So, Xena will coach four players and Zara will coach two players.
The average rating of all eight players is 4. So, the total rating is 32. Only P-5 and P-7 got the same rating and all the remaining players got a unique rating. Let the rating got by P-5 and P-7 be x. According to the problem,1+2+3+..+7+n = 32
n = 4
So the rating of P-5 and P-7 is 4 each. P-2 got the highest rating which means he got a rating of 7. P-4’s rating is double that of P-8 but less than P-5, so the rating of P-4 must be 2 and the rating of P-8 must be 1. Because P-4’s rating cannot be 4 and it cannot be 6. With this information, we get the following table.
The only ratings remaining for the players are 3, 5, and 6. It is given that the average ratings given by Yuki is two more than that of Zara. The average rating given by Zara = 4. So, the average rating given by Yuki = is 6. One player got a rating of 7 so the other must get a rating of 5. So, P-6 will be coached by Yuki and get a rating of 5. P-8 will be coached by Xena and P-1 and P-3 will get a rating of 3 and 6 in any order. Finally, we get the following table.
Q5: Who all were the players trained by Xena?
(a) Player-1, Player-3, Player-4, Player-6
(b) Player-1, Player-3, Player-4, Player-8
(c) Player-1, Player-3, Player-4
(d) Player-1, Player-4, Player-6, Player-8
Ans: (b)
Sol: Let the 8 players be P-1 through P-8, Now it is given that each coach trained at least two players and the number of players coached by Xena is more than Yuki. So the only combination of players trained by the three coaches Xena, Yuki, and Zara must be either 3, 2, and 3 respectively, or 4, 2, and 2 respectively.
From statement 2 we can say that P-1 and P-4 were trained by Xena because one is odd and the other is even, and the only coach who can coach both odd and even-numbered is Xena. P-2, P-3, and P-5 were all coached by different coaches. 3 and 5 both are odd so these two players must be coached by Xena and Zara one each in any order. P-2 will be trained by Yuki. Both P-5 and P-7 were trained by the same coach.
With this information, we can get the following table.
From the above table, we can say that the possible players coached by Zara must be 5 and P-7 or only P-3 which is not possible because each coach coached at least two players hence with this we can say that players 5 and 7 were coached by Zara and P-3 was coached by Xena. So, Xena will coach four players and Zara will coach two players.
The average rating of all eight players is 4. So, the total rating is 32. Only P-5 and P-7 got the same rating and all the remaining players got a unique rating. Let the rating got by P-5 and P-7 be x. According to the problem,1+2+3+..+7+n = 32
n = 4
So the rating of P-5 and P-7 is 4 each. P-2 got the highest rating which means he got a rating of 7. P-4’s rating is double that of P-8 but less than P-5, so the rating of P-4 must be 2 and the rating of P-8 must be 1. Because P-4’s rating cannot be 4 and it cannot be 6. With this information, we get the following table.
The only ratings remaining for the players are 3, 5, and 6. It is given that the average ratings given by Yuki is two more than that of Zara. The average rating given by Zara = 4. So, the average rating given by Yuki = is 6. One player got a rating of 7 so the other must get a rating of 5. So, P-6 will be coached by Yuki and get a rating of 5. P-8 will be coached by Xena and P-1 and P-3 will get a rating of 3 and 6 in any order. Finally, we get the following table.
2023
Passage - 1
Instructions
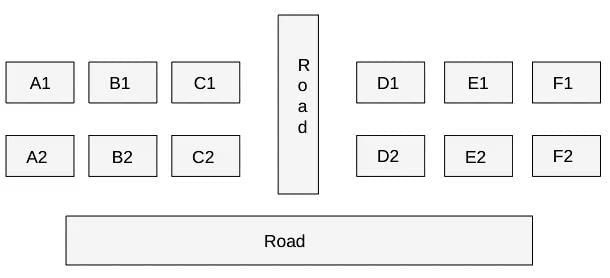
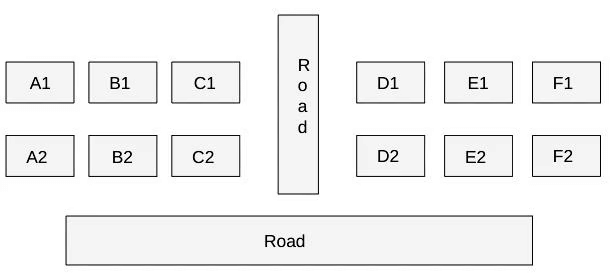
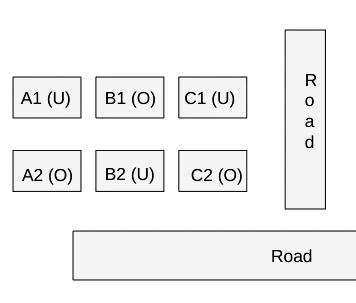
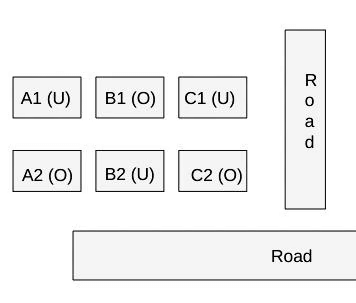
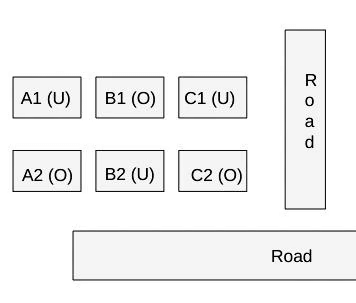
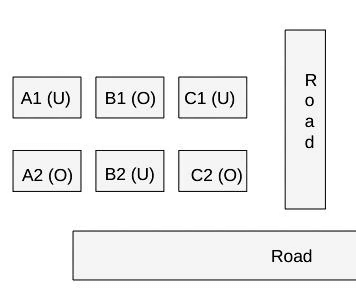
The schematic diagram below shows 12 rectangular houses in a housing complex. House numbers are mentioned in the rectangles representing the houses. The houses are located in six columns - Column-A through Column-F, and two rows - Row-1 and Row-2. The houses are divided into two blocks - Block XX and Block YY. The diagram also shows two roads, one passing in front of the houses in Row-2 and another between the two blocks.
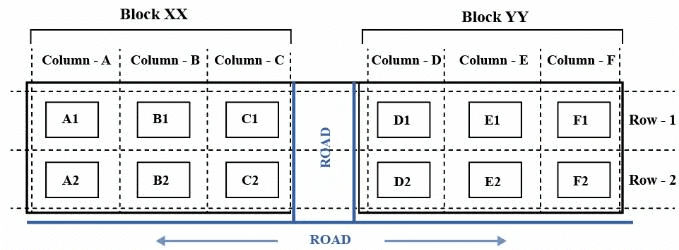
Some of the houses are occupied. The remaining ones are vacant and are the only ones available for sale.
The road adjacency value of a house is the number of its sides adjacent to a road. For example, the road adjacency values of C2, F2, and B1 are 2, 1, and 0, respectively. The neighbour count of a house is the number of sides of that house adjacent to occupied houses in the same block. For example, E1 and C1 can have the maximum possible neighbour counts of 3 and 2, respectively.
The base price of a vacant house is Rs. 10 lakhs if the house does not have a parking space, and Rs. 12 lakhs if it does. The quoted price (in lakhs of Rs.) of a vacant house is calculated as (base price) + 5 × (road adjacency value) + 3 × (neighbour count). The following information is also known.
- The maximum quoted price of a house in Block XX is Rs. 24 lakhs. The minimum quoted price of a house in block YY is Rs. 15 lakhs, and one such house is in Column-E.
- Row-1 has two occupied houses, one in each block.
- Both houses in Column-E are vacant. Each of Column-D and Column-F has at least one occupied house.
- There is only one house with parking space in Block YY.
Q1: How many houses are vacant in Block XX?
Ans: 3
Sol:
It is given that some of the houses are occupied. The remaining ones are vacant and are the only ones available for sale.
The base price of a vacant house is Rs. 10 lakhs if the house does not have a parking space, and Rs. 12 lakhs if it does. The quoted price (in lakhs of Rs.) of a vacant house is calculated as (base price) + 5 × (road adjacency value) + 3 × (neighbor count).
It is also known that the maximum quoted price of a house in Block XX is Rs. 24 lakhs
Hence, there can be two cases for the maximum quoted price of a house in block XX.Case 1: House with parking space:
=> 12+5a+3b = 24 => 5a+3b = 12 ( a = road adjacency value, b= neighbor count)
The only value for which the equation satisfies is (a = 0, and b=4). But the value of b can't be 4 because the maximum neighbor count can be at most 3.
Hence, case 1 is invalid.Case 2: House without parking space:
=> 10+5a+3b = 24 => 5a+3b = 14
=> (a, b) = (1, 3)Hence, the house must have 3 neighbors and 1 road connected to it. Hence, the only possible case is B2. Therefore, the neighbor houses of B2, which are (B1, A2, and C2) are also occupied.
It is known that Row 1 has two occupied houses, one in each block. Since B1 is already occupied, it implies A1, and C1 are vacant.
Hence, the configuration of block XX is given below: (Where U = Unoccupied/ Vacant, and U = Occupied)
Now for block YY, we know that both houses in Column E are vacant. Each of Column-D and Column-F has at least one occupied house. There is only one house with parking space in Block YY.
It is also known that the minimum quoted price of a house in block YY is Rs. 15 lakhs, and one such house is in Column E.Case 1: The minimum quoted house is E2:
We know that the road adjacency of E2 is 1, hence we can calculate whether the house has parking space or not, and the neighbor count (b)
If the house has parking space, then: 12+5*1+3*b = 15 => 3b = -2 (which is not possible)
Hence, the house has no parking space => 10+5*1+3b = 15 => b = 0
b = 0 implies all the neighbor house of E2 is vacant, which are (E1, D2, and F2).
It is known that each of Column-D and Column-F has at least one occupied house, which implies D1, and F1 must be occupied.
But D1 and F1 can't be occupied together since the total number of occupied houses in Row 1 is 2 (one in each block).
Hence, This case is invalid.Case 2: The minimum quoted house is E1:
We know that the road adjacency of E1 is 0, hence we can calculate whether the house has parking space or not, and the neighbor count (b).
i) If the house has no working space, then: 10+5*0+3b = 15 => b = 5/3 (this is not possible since b has to be an integer value)
Hence, the house has parking space => 12+5*0+3b = 15 => b = 1 => One neighbor house is occupied among D1 and F1.
We already know that E2 is vacant. Among the houses D2, and F2, at least one must be occupied since each of Column-D and Column-F has at least one occupied house.
Therefore, the final diagram is given below:
From the diagram, we can see that 3 houses are vacant in block XX.
Q2: Which of the following houses is definitely occupied?
(a) A1
(b) D2
(c) B1
(d) F2
Ans: (c)
Sol:
It is given that some of the houses are occupied. The remaining ones are vacant and are the only ones available for sale.
The base price of a vacant house is Rs. 10 lakhs if the house does not have a parking space, and Rs. 12 lakhs if it does. The quoted price (in lakhs of Rs.) of a vacant house is calculated as (base price) + 5 × (road adjacency value) + 3 × (neighbor count).
It is also known that the maximum quoted price of a house in Block XX is Rs. 24 lakhs
Hence, there can be two cases for the maximum quoted price of a house in block XX.
Case 1: House with parking space:
=> 12+5a+3b = 24 => 5a+3b = 12 ( a = road adjacency value, b= neighbor count)
The only value for which the equation satisfies is (a = 0, and b=4). But the value of b can't be 4 because the maximum neighbor count can be at most 3.
Hence, case 1 is invalid.
Case 2: House without parking space:
=> 10+5a+3b = 24 => 5a+3b = 14
=> (a, b) = (1, 3)
Hence, the house must have 3 neighbors and 1 road connected to it. Hence, the only possible case is B2. Therefore, the neighbor houses of B2, which are (B1, A2, and C2) are also occupied.
It is known that Row 1 has two occupied houses, one in each block. Since B1 is already occupied, it implies A1, and C1 are vacant.
Hence, the configuration of block XX is given below: (Where U = Unoccupied/ Vacant, and U = Occupied)
Now for block YY, we know that both houses in Column E are vacant. Each of Column-D and Column-F has at least one occupied house. There is only one house with parking space in Block YY.
It is also known that the minimum quoted price of a house in block YY is Rs. 15 lakhs, and one such house is in Column E.
Case 1: The minimum quoted house is E2:
We know that the road adjacency of E2 is 1, hence we can calculate whether the house has parking space or not, and the neighbor count (b)
If the house has parking space, then: 12+5*1+3*b = 15 => 3b = -2 (which is not possible)
Hence, the house has no parking space => 10+5*1+3b = 15 => b = 0
b = 0 implies all the neighbor house of E2 is vacant, which are (E1, D2, and F2).
It is known that each of Column-D and Column-F has at least one occupied house, which implies D1, and F1 must be occupied.
But D1 and F1 can't be occupied together since the total number of occupied houses in Row 1 is 2 (one in each block).
Hence, This case is invalid.
Case 2: The minimum quoted house is E1:
We know that the road adjacency of E1 is 0, hence we can calculate whether the house has parking space or not, and the neighbor count (b).
i) If the house has no working space, then: 10+5*0+3b = 15 => b = 5/3 (this is not possible since b has to be an integer value)
Hence, the house has parking space => 12+5*0+3b = 15 => b = 1 => One neighbor house is occupied among D1 and F1.
We already know that E2 is vacant. Among the houses D2, and F2, at least one must be occupied since each of Column-D and Column-F has at least one occupied house.
Therefore, the final diagram is given below:
From the diagram, we can see that B1 is definitely occupied. The rest opinions are not definitely correct.
The correct option is C
Q3: Which of the following options best describes the number of vacant houses in Row-2?
(a) Exactly 3
(b) Either 3 or 4
(c) Exactly 2
(d) Either 2 or 3
Ans: (d)
Sol:
It is given that some of the houses are occupied. The remaining ones are vacant and are the only ones available for sale.
The base price of a vacant house is Rs. 10 lakhs if the house does not have a parking space, and Rs. 12 lakhs if it does. The quoted price (in lakhs of Rs.) of a vacant house is calculated as (base price) + 5 × (road adjacency value) + 3 × (neighbor count).
It is also known that the maximum quoted price of a house in Block XX is Rs. 24 lakhs
Hence, there can be two cases for the maximum quoted price of a house in block XX.
Case 1: House with parking space:
=> 12+5a+3b = 24 => 5a+3b = 12 ( a = road adjacency value, b= neighbor count)
The only value for which the equation satisfies is (a = 0, and b=4). But the value of b can't be 4 because the maximum neighbor count can be at most 3.
Hence, case 1 is invalid.
Case 2: House without parking space:
=> 10+5a+3b = 24 => 5a+3b = 14
=> (a, b) = (1, 3)
Hence, the house must have 3 neighbors and 1 road connected to it. Hence, the only possible case is B2. Therefore, the neighbor houses of B2, which are (B1, A2, and C2) are occupied.
It is known that Row 1 has two occupied houses, one in each block. Since B1 is already occupied, it implies A1, and C1 are vacant.
Hence, the configuration of block XX is given below: (Where U = Unoccupied/ Vacant, and U = Occupied)
Now for block YY, we know that both houses in Column E are vacant. Each of Column-D and Column-F has at least one occupied house. There is only one house with parking space in Block YY.
It is also known that the minimum quoted price of a house in block YY is Rs. 15 lakhs, and one such house is in Column E.
Case 1: The minimum quoted house is E2:
We know that the road adjacency of E2 is 1, hence we can calculate whether the house has parking space or not, and the neighbor count (b)
If the house has parking space, then: 12+5*1+3*b = 15 => 3b = -2 (which is not possible)
Hence, the house has no parking space => 10+5*1+3b = 15 => b = 0
b = 0 implies all the neighbor house of E2 is vacant, which are (E1, D2, and F2).
It is known that each of Column-D and Column-F has at least one occupied house, which implies D1, and F1 must be occupied.
But D1 and F1 can't be occupied together since the total number of occupied houses in Row 1 is 2 (one in each block).
Hence, This case is invalid.
Case 2: The minimum quoted house is E1:
We know that the road adjacency of E1 is 0, hence we can calculate whether the house has parking space or not, and the neighbor count (b).
i) If the house has no working space, then: 10+5*0+3b = 15 => b = 5/3 (this is not possible since b has to be an integer value)
Hence, the house has parking space => 12+5*0+3b = 15 => b = 1 => One neighbor house is occupied among D1 and F1.
Let's take the case that house D1 is occupied and F1 is empty. In that case, the value of house F1 would be 10(there is no parking space)+ (5*0) + (3*the number of neighbours)
Here, even if we take the number of neighbours to be 1, which is maximum for F1 in this case, the value of F1 would be a maximum of 13. This is lower than the lowest value house in block YY. Therefore, F1 cannot be empty.
Let us see the other scenario of D1 being unoccupied.
Here, the value of D1 can be 15 or 18 depending on if D2 is unoccupied or occupied respectively.We do not know the status of houses D2 and F2.
Therefore, the final diagram is given below:
From the diagram, we can say that the number of vacant houses in Row 2 in Block XX is 1, and the number of vacant houses in Row 2 in Block YY is either 1 or 2.Hence, the total number of vacant houses is either 2 or 3
The correct option is D
Q4: What is the maximum possible quoted price (in lakhs of Rs.) for a vacant house in Column-E?
Ans: 21
Sol:
It is given that some of the houses are occupied. The remaining ones are vacant and are the only ones available for sale.
The base price of a vacant house is Rs. 10 lakhs if the house does not have a parking space, and Rs. 12 lakhs if it does. The quoted price (in lakhs of Rs.) of a vacant house is calculated as (base price) + 5 × (road adjacency value) + 3 × (neighbor count).
It is also known that the maximum quoted price of a house in Block XX is Rs. 24 lakhs
Hence, there can be two cases for the maximum quoted price of a house in block XX.
Case 1: House with parking space:
=> 12+5a+3b = 24 => 5a+3b = 12 ( a = road adjacency value, b= neighbor count)
The only value for which the equation satisfies is (a = 0, and b=4). But the value of b can't be 4 because the maximum neighbor count can be at most 3.
Hence, case 1 is invalid.
Case 2: House without parking space:
=> 10+5a+3b = 24 => 5a+3b = 14
=> (a, b) = (1, 3)
Hence, the house must have 3 neighbors and 1 road connected to it. Hence, the only possible case is B2. Therefore, the neighbor houses of B2, which are (B1, A2, and C2) are also occupied.
It is known that Row 1 has two occupied houses, one in each block. Since B1 is already occupied, it implies A1, and C1 are vacant.
Hence, the configuration of block XX is given below: (Where U = Unoccupied/ Vacant, and U = Occupied)
Now for block YY, we know that both houses in Column E are vacant. Each of Column-D and Column-F has at least one occupied house. There is only one house with parking space in Block YY.
It is also known that the minimum quoted price of a house in block YY is Rs. 15 lakhs, and one such house is in Column E.
Case 1: The minimum quoted house is E2:
We know that the road adjacency of E2 is 1, hence we can calculate whether the house has parking space or not, and the neighbor count (b)
If the house has parking space, then: 12+5*1+3*b = 15 => 3b = -2 (which is not possible)
Hence, the house has no parking space => 10+5*1+3b = 15 => b = 0
b = 0 implies all the neighbor house of E2 is vacant, which are (E1, D2, and F2).
It is known that each of Column-D and Column-F has at least one occupied house, which implies D1, and F1 must be occupied.
But D1 and F1 can't be occupied together since the total number of occupied houses in Row 1 is 2 (one in each block).
Hence, This case is invalid.
Case 2: The minimum quoted house is E1:
We know that the road adjacency of E1 is 0, hence we can calculate whether the house has parking space or not, and the neighbor count (b).
i) If the house has no working space, then: 10+5*0+3b = 15 => b = 5/3 (this is not possible since b has to be an integer value)
Hence, the house has parking space => 12+5*0+3b = 15 => b = 1 => One neighbor house is occupied among D1 and F1.
We already know that E2 is vacant. Among the houses D2, and F2, at least one must be occupied since each of Column-D and Column-F has at least one occupied house.
Therefore, the final diagram is given below:
From the diagram, the vacant house with the maximum possible quoted price in column E is E2 when both D2 and F2 are occupied.
The maximum possible quoted price of E2 is 10+5*1+3*2 = 21 Lacs. ( E2 has no parking space because E1 has the parking space and it is given that there is only one house with parking space in Block YY.)
Q5: Which house in Block YY has parking space?
(a) E1
(b) F2
(c) E2
(d) F1
Ans: (a)
Sol:
It is given that some of the houses are occupied. The remaining ones are vacant and are the only ones available for sale.
The base price of a vacant house is Rs. 10 lakhs if the house does not have a parking space, and Rs. 12 lakhs if it does. The quoted price (in lakhs of Rs.) of a vacant house is calculated as (base price) + 5 × (road adjacency value) + 3 × (neighbor count).
It is also known that the maximum quoted price of a house in Block XX is Rs. 24 lakhs
Hence, there can be two cases for the maximum quoted price of a house in block XX.
Case 1: House with parking space:
=> 12+5a+3b = 24 => 5a+3b = 12 ( a = road adjacency value, b= neighbor count)
The only value for which the equation satisfies is (a = 0, and b=4). But the value of b can't be 4 because the maximum neighbor count can be at most 3.
Hence, case 1 is invalid.
Case 2: House without parking space:
=> 10+5a+3b = 24 => 5a+3b = 14
=> (a, b) = (1, 3)
Hence, the house must have 3 neighbors and 1 road connected to it. Hence, the only possible case is B2. Therefore, the neighbor houses of B2, which are (B1, A2, and C2) are also occupied.
It is known that Row 1 has two occupied houses, one in each block. Since B1 is already occupied, it implies A1, and C1 are vacant.
Hence, the configuration of block XX is given below: (Where U = Unoccupied/ Vacant, and U = Occupied)
Now for block YY, we know that both houses in Column E are vacant. Each of Column-D and Column-F has at least one occupied house. There is only one house with parking space in Block YY.
It is also known that the minimum quoted price of a house in block YY is Rs. 15 lakhs, and one such house is in Column E.
Case 1: The minimum quoted house is E2:
We know that the road adjacency of E2 is 1, hence we can calculate whether the house has parking space or not, and the neighbor count (b)
If the house has parking space, then: 12+5*1+3*b = 15 => 3b = -2 (which is not possible)
Hence, the house has no parking space => 10+5*1+3b = 15 => b = 0
b = 0 implies all the neighbor house of E2 is vacant, which are (E1, D2, and F2).
It is known that each of Column-D and Column-F has at least one occupied house, which implies D1, and F1 must be occupied.
But D1 and F1 can't be occupied together since the total number of occupied houses in Row 1 is 2 (one in each block).
Hence, This case is invalid.
Case 2: The minimum quoted house is E1:
We know that the road adjacency of E1 is 0, hence we can calculate whether the house has parking space or not, and the neighbor count (b).
i) If the house has no working space, then: 10+5*0+3b = 15 => b = 5/3 (this is not possible since b has to be an integer value)
Hence, the house has parking space => 12+5*0+3b = 15 => b = 1 => One neighbor house is occupied among D1 and F1.
We already know that E2 is vacant. Among the houses D2, and F2, at least one must be occupied since each of Column-D and Column-F has at least one occupied house.
Therefore, the final diagram is given below:
From the diagram, we can see that E1 has the parking space (case 2).
The correct option is A
Passage -2
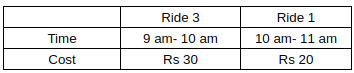
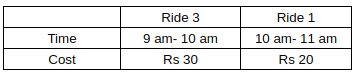
Anjali, Bipasha, and Chitra visited an entertainment park that has four rides. Each ride lasts one hour and can accommodate one visitor at one point. All rides begin at 9 am and must be completed by 5 pm except for Ride-3, for which the last ride has to be completed by 1 pm. Ride gates open every 30 minutes, e.g. 10 am, 10:30 am, and so on. Whenever a ride gate opens, and there is no visitor inside, the first visitor waiting in the queue buys the ticket just before taking the ride. The ticket prices are Rs. 20, Rs. 50, Rs. 30 and Rs. 40 for Rides 1 to 4, respectively. Each of the three visitors took at least one ride and did not necessarily take all rides. None of them took the same ride more than once. The movement time from one ride to another is negligible, and a visitor leaves the ride immediately after the completion of the ride. No one takes a break inside the park unless mentioned explicitly.
The following information is also known.
- Chitra never waited in the queue and completed her visit by 11 am after spending Rs. 50 to pay for the ticket(s).
- Anjali took Ride-1 at 11 am after waiting for 30 mins for Chitra to complete it. It was the only ride where Anjali waited.
- Bipasha began her first of three rides at 11:30 am. All three visitors incurred the same amount of ticket expense by 12:15 pm.
- The last ride taken by Anjali and Bipasha was the same, where Bipasha waited 30 mins for Anjali to complete her ride.
Before standing in the queue for that ride, Bipasha took a 1-hour coffee break after completing her previous ride.
Q1: How many rides did Anjali and Chitra take in total?
Ans: 6
Sol: Consider Statement 2: Anjali took Ride-1 at 11 am after waiting for 30 minutes for Chitra to complete it. It was the only ride where Anjali waited.This implies that Chitra took Ride 1 at 10 am. Now we also know that she spent Rs 50 and that she left at 11 am. Now, since she did one ride costing Rs 20 at 10, she must have taken Ride-3 at 9 am.
So we get the following table for Chitra.
Now we know that Chitra and Anjali spent Rs 50 before 12:15 pm. It is not possible for Anjali to go on Ride-3 at 10 am as we know that she was waiting for 30 minutes before taking Ride-1 (She was waiting from 10:30 am).
Now, since we know that Ride-1 was the only ride for which she waited, we can say that she took Ride-1 at 11 am and started Ride-3 at 12 am
So we get the following table for Anjali.
Now, we know that Bipasha started her first ride at 11:30 am. We also know that they all spent Rs 50 before 12:15 pm.
Therefore, the first ride Bipasha takes will be Ride-2, costing Rs 50.
So we get the following table for Bipasha.
We know that Ride 3 stops at 1 pm. So the last ride taken by Anjali will either be Ride-2 or Ride-4. Now, considering Statement 4,we know that the last ride taken by Anjali and Bipasha was same and that Bipasha rode it after Anjali. So their last ride can’t be 2.
So the last ride of both Bipasha and Anjali will be 4.
Now if we assume that immediately after ending Ride-3, Anjali goes to Ride-4, then the last ride of Bipasha will be Ride-4 from 2 pm - 3 pm. But we know that Bipasha rode 3 rides. So this case is not possible.
Since Anjali didn’t have any break or waiting time, the only ride she can ride at 1 pm will be Ride 2 and then she will go on Ride-4 from 2 pm to 3 pm.
So we get the following table for Anjali:
Now we know that the last ride that Bipasha took was Ride-4 and that she had a gap of 1.5 hrs before it. This is only possible when she takes one ride between Ride-2 and Ride-4. Since Ride-3 is closed at 1 pm, she can only take Ride 1. So we get the following table for her.
Anjali took 4 rides, and Chitra took 2 rides. Therefore the correct answer is 6
Q2: What was the total amount spent on tickets (in Rs.) by Anjali?
Ans: 140
Sol: Consider Statement 2: Anjali took Ride-1 at 11 am after waiting for 30 minutes for Chitra to complete it. It was the only ride where Anjali waited.This implies that Chitra took Ride 1 at 10 am. Now we also know that she spent Rs 50 and that she left at 11 am. Now, since she did one ride costing Rs 20 at 10, she must have taken Ride-3 at 9 am.
So we get the following table for Chitra.
Now we know that Chitra and Anjali spent Rs 50 before 12:15 pm. It is not possible for Anjali to go on Ride-3 at 10 am as we know that she was waiting for 30 minutes before taking Ride-1 (She was waiting from 10:30 am).
Now, since we know that Ride-1 was the only ride for which she waited, we can say that she took Ride-1 at 11 am and started Ride-3 at 12 am
So we get the following table for Anjali.
Now, we know that Bipasha started her first ride at 11:30 am. We also know that they all spent Rs 50 before 12:15 pm.
Therefore, the first ride Bipasha takes will be Ride-2, costing Rs 50.
So we get the following table for Bipasha.
We know that Ride 3 stops at 1 pm. So the last ride taken by Anjali will either be Ride-2 or Ride-4. Now, considering Statement 4,we know that the last ride taken by Anjali and Bipasha was same and that Bipasha rode it after Anjali. So their last ride can’t be 2.
So the last ride of both Bipasha and Anjali will be 4.
Now if we assume that immediately after ending Ride-3, Anjali goes to Ride-4, then the last ride of Bipasha will be Ride-4 from 2 pm - 3 pm. But we know that Bipasha rode 3 rides. So this case is not possible.
Since Anjali didn’t have any break or waiting time, the only ride she can ride at 1 pm will be Ride 2 and then she will go on Ride-4 from 2 pm to 3 pm.
So we get the following table for Anjali:
Now we know that the last ride that Bipasha took was Ride-4 and that she had a gap of 1.5 hrs before it. This is only possible when she takes one ride between Ride-2 and Ride-4. Since Ride-3 is closed at 1 pm, she can only take Ride 1. So we get the following table for her.
As we can see from the table of Anjali she spent a total of 20 + 30 + 50 + 40 = 140
Therefore the required answer is 140
Passage - 3
Faculty members in a management school can belong to one of four departments - Finance and Accounting (F&A), Marketing and Strategy (M&S), Operations and Quants (O&Q) and Behaviour and Human Resources (B&H). The numbers of faculty members in F&A, M&S, O&Q and B&H departments are 9, 7, 5 and 3 respectively.
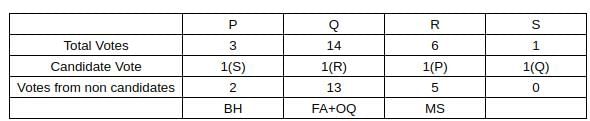
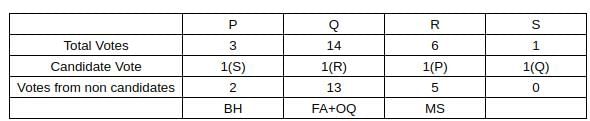
Prof. Pakrasi, Prof. Qureshi, Prof. Ramaswamy and Prof. Samuel are four members of the school's faculty who were candidates for the post of the Dean of the school. Only one of the candidates was from O&Q.
Every faculty member, including the four candidates, voted for the post. In each department, all the faculty members who were not candidates voted for the same candidate. The rules for the election are listed below.
1. There cannot be more than two candidates from a single department.
2. A candidate cannot vote for himself/herself.
3. Faculty members cannot vote for a candidate from their own department.
After the election, it was observed that Prof. Pakrasi received 3 votes, Prof. Qureshi received 14 votes, Prof. Ramaswamy received 6 votes and Prof. Samuel received 1 vote. Prof. Pakrasi voted for Prof. Ramaswamy, Prof. Qureshi for Prof. Samuel, Prof. Ramaswamy for Prof. Qureshi and Prof. Samuel for Prof. Pakrasi.
Q1: Which two candidates can belong to the same department?
(a) Prof. Pakrasi and Prof. Qureshi
(b) Prof. Pakrasi and Prof. Samuel
(c) Prof. Qureshi and Prof. Ramaswamy
(d) Prof. Ramaswamy and Prof. Samuel
Ans: a
Sol: Now, we know there is only 1 candidate from OQ, which means that the number of non-candidate voters in OQ will be 4.
We also know that the non-candidates in a particular department voted as a block, and we also know that the least number of non-candidate voters in a particular department can be 1 (BH, 3-2 faculty).
Now, we also know that R got 5 votes from non-candidates.
Now we can write 5 as
(i) 5
(ii) 4+1
(iii) 3+2
Considering case (i) 4+1. This is only possible when there is 1 candidate from OQ, and there are 2 candidates from BH. This implies that the number of candidates in FA and MQ is 1. Now, if we consider FA and MQ and put only 1 candidate there, it implies that there are 15 non-candidate voters between them. Now we know this is not possible since the maximum number of non-candidate voters a candidate can get is 13. (Please note that non-candidates of a particular department vote as a block).
On similar grounds, we can eliminate Case (iii) as it also implies there is only 1 candidate in FA and MQ.
Now, considering Case (i), we know that 5+0 will happen only one when there are 5 non-candidates in a single department. This is only possible in MS (Out of 7, there will be 2 candidates and 5 non-candidates).
So we can conclude that MS has 2 candidates and that they voted Prof. R…….(i)
We also know that Prof P got 2 votes from Non-candidates. This is only possible when BH has 1 candidate.
So, we can conclude that the number of professors in FA, MS, OQ, BH is 0,2,1,1
Thus, we get the following table:
Now, if we consider Department MS, we know that there are 2 candidates from MS and R can’t be one of them as the people in that department voted for him….. (3 rd condition).
So the possible combinations of candidates in MS are (P,Q), (Q,S), (P,S).
Now we also know that no one can vote for a candidate in their own department, so we can eliminate (P,S) and (Q,S) as we know that S voted for P and Q voted for S).
So we can infer that P and Q are from MS.
Now, among the given options, Only Option A is true. Therefore, Option A is the correct answer.
Q2: Which of the following can be the number of votes that Prof. Qureshi received from a single department?
(a) 7
(b) 6
(c) 8
(d) 9
Ans: d
Sol: Now, we know there is only 1 candidate from OQ, which means that the number of non-candidate voters in OQ will be 4.
We also know that the non-candidates in a particular department voted as a block, and we also know that the least number of non-candidate voters in a particular department can be 1 (BH, 3-2 faculty).
Now, we also know that R got 5 votes from non-candidates.
Now we can write 5 as
(i) 5
(ii) 4+1
(iii) 3+2
Considering case (i) 4+1. This is only possible when there is 1 candidate from OQ, and there are 2 candidates from BH. This implies that the number of candidates in FA and MQ is 1. Now, if we consider FA and MQ and put only 1 candidate there, it implies that there are 15 non-candidate voters between them. Now, we know this is not possible since the maximum number of non-candidate voters a candidate can get is 13. (Please note that non-candidates of a particular department vote as a block).
On similar grounds, we can eliminate Case (iii) as it also implies there is only 1 candidate in FA and MQ.
Now, considering Case (i), we know that 5+0 will happen only once when there are 5 non-candidates in a single department. This is only possible in MS (Out of 7, there will be 2 candidates and 5 non-candidates).
So we can conclude that MS has 2 candidates and that they voted Prof. R…….(i)
We also know that Prof P got 2 votes from Non-candidates. This is only possible when BH has 1 candidate.
So, we can conclude that the number of professors in FA, MS, OQ, BH is 0,2,1,1
Thus, we get the following table:
Now, if we consider Department MS, we know that there are 2 candidates from MS and R can’t be one of them as the people in that department voted for him….. (3 rd condition).
So, the possible combinations of candidates in MS are (P,Q), (Q,S), (P,S).
Now we also know that no one can vote for a candidate in their own department, so we can eliminate (P,S) and (Q,S) as we know that S voted for P and Q voted for S).
So, we can infer that P and Q are from MS.
Now, we can see that the number of votes that Prof Qureshi received from a single department can be 9 or 5 (if R is from OQ) or 4 (if R is not from OQ).
So, among the options, only Option D can be true. Therefore, Option D is the correct answer.
Q3: If Prof. Samuel belongs to B&H, which of the following statements is/are true?
Statement A: Prof. Pakrasi belongs to M&S.
Statement B: Prof. Ramaswamy belongs to O&Q
(a) Neither statement A nor statement B
(b) Only statement B
(c) Only statement A
(d) Both statements A and B
Ans: d
Sol: Now, we know there is only 1 candidate from OQ, which means that the number of non-candidate voters in OQ will be 4.We also know that the non-candidates in a particular department voted as a block, and we also know that the least number of non-candidate voters in a particular department can be 1 (BH, 3-2 faculty).
Now, we also know that R got 5 votes from non-candidates.
Now we can write 5 as
(i) 5
(ii) 4+1
(iii) 3+2
Considering case (i) 4+1. This is only possible when there is 1 candidate from OQ, and there are 2 candidates from BH. This implies that the number of candidates in FA and MQ is 1. Now, if we consider FA and MQ and put only 1 candidate there, it implies that there are 15 non-candidate voters between them. Now we know this is not possible since the maximum number of non-candidate voters a candidate can get is 13. (Please note that non-candidates of a particular department vote as a block).
On similar grounds, we can eliminate Case (iii) as it also implies there is only 1 candidate in FA and MQ.
Now, considering Case (i), we know that 5+0 will happen only one when there are 5 non-candidates in a single department. This is only possible in MS (Out of 7, there will be 2 candidates and 5 non-candidates).
So we can conclude that MS has 2 candidates and that they voted Prof. R…….(i)
We also know that Prof P got 2 votes from Non-candidates. This is only possible when BH has 1 candidate.
So, we can conclude that the number of professors in FA, MS, OQ, BH is 0,2,1,1
Thus, we get the following table:
Now, if we consider Department MS, we know that there are 2 candidates from MS and R can’t be one of them as the people in that department voted for him….. (3 rd condition).
So the possible combinations of candidates in MS are (P,Q), (Q,S), (P,S).
Now we also know that no one can vote for a candidate in their own department, so we can eliminate (P,S) and (Q,S) as we know that S voted for P and Q voted for S).
So we can infer that P and Q are from MS.
We have been told Prof Samuel belongs to B&H. So we have to consider only Case 1. In Case 1 we can see that Prof Prakash belongs to MS and Prof Ramaswamy belongs to OQ.
Therefore, both the statements are true.
So, the correct answer is Option D
Q4: What best can be concluded about the candidate from O&Q?
(a) It was Prof. Samuel.
(b) It was either Prof. Ramaswamy or Prof. Samuel.
(c) It was Prof. Ramaswamy.
(d) It was either Prof. Pakrasi or Prof. Qureshi.
Ans: b
Sol: Now, we know there is only 1 candidate from OQ, which means that the number of non-candidate voters in OQ will be 4.We also know that the non-candidates in a particular department voted as a block, and we also know that the least number of non-candidate voters in a particular department can be 1 (BH, 3-2 faculty).
Now, we also know that R got 5 votes from non-candidates.Now we can write 5 as
(i) 5
(ii) 4+1
(iii) 3+2
Considering case (i) 4+1. This is only possible when there is 1 candidate from OQ, and there are 2 candidates from BH. This implies that the number of candidates in FA and MQ is 1. Now, if we consider FA and MQ and put only 1 candidate there, it implies that there are 15 non-candidate voters between them. Now we know this is not possible since the maximum number of non-candidate voters a candidate can get is 13. (Please note that non-candidates of a particular department vote as a block).
On similar grounds, we can eliminate Case (iii) as it also implies there is only 1 candidate in FA and MQ.
Now, considering Case (i), we know that 5+0 will happen only one when there are 5 non-candidates in a single department. This is only possible in MS (Out of 7, there will be 2 candidates and 5 non-candidates).
So we can conclude that MS has 2 candidates and that they voted Prof. R…….(i)
We also know that Prof P got 2 votes from Non-candidates. This is only possible when BH has 1 candidate.
So, we can conclude that the number of professors in FA, MS, OQ, BH is 0,2,1,1
Thus, we get the following table:
Now, if we consider Department MS, we know that there are 2 candidates from MS and R can’t be one of them as the people in that department voted for him….. (3 rd condition).
So the possible combinations of candidates in MS are (P,Q), (Q,S), (P,S).
Now we also know that no one can vote for a candidate in their own department, so we can eliminate (P,S) and (Q,S) as we know that S voted for P and Q voted for S).
So we can infer that P and Q are from MS.
From the 2 cases, we can see that the candidate from OQ can either be Prof Ramaswamy or Prof Samuel.
Therefore, the correct answer is Option B.
Q5: Which of the following statements is/are true?
Statement A: Non-candidates from M&S voted for Prof. Qureshi.
Statement B: Non-candidates from F&A voted for Prof. Qureshi.
(a) Both statements A and B
(b) Only statement B
(c) Only statement A
(d) Neither statement A nor statement B
Ans: b
Sol: Now, we know there is only 1 candidate from OQ, which means that the number of non-candidate voters in OQ will be 4.We also know that the non-candidates in a particular department voted as a block, and we also know that the least number of non-candidate voters in a particular department can be 1 (BH, 3-2 faculty).
Now, we also know that R got 5 votes from non-candidates.
Now we can write 5 as
(i) 5
(ii) 4+1
(iii) 3+2
Considering case (i) 4+1. This is only possible when there is 1 candidate from OQ, and there are 2 candidates from BH. This implies that the number of candidates in FA and MQ is 1. Now, if we consider FA and MQ and put only 1 candidate there, it implies that there are 15 non-candidate voters between them. Now we know this is not possible since the maximum number of non-candidate voters a candidate can get is 13. (Please note that non-candidates of a particular department vote as a block).
On similar grounds, we can eliminate Case (iii) as it also implies there is only 1 candidate in FA and MQ.
Now, considering Case (i), we know that 5+0 will happen only one when there are 5 non-candidates in a single department. This is only possible in MS (Out of 7, there will be 2 candidates and 5 non-candidates).
So we can conclude that MS has 2 candidates and that they voted Prof. R…….(i)
We also know that Prof P got 2 votes from Non-candidates. This is only possible when BH has 1 candidate.
So, we can conclude that the number of professors in FA, MS, OQ, BH is 0,2,1,1
Thus, we get the following table:
Now, if we consider Department MS, we know that there are 2 candidates from MS and R can’t be one of them as the people in that department voted for him….. (3 rd condition).
So the possible combinations of candidates in MS are (P,Q), (Q,S), (P,S).
Now we also know that no one can vote for a candidate in their own department, so we can eliminate (P,S) and (Q,S) as we know that S voted for P and Q voted for S).
So we can infer that P and Q are from MS.
Since Prof Qureshi belongs to MS, non-candidates from MS can't vote for him. We can see that the non-candidates from FA voted for him. So, only statement B is true. Therefore, the correct answer is Option B.
2022
Passage - 1
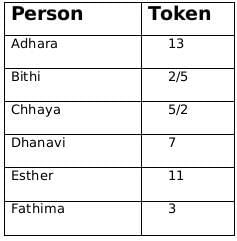
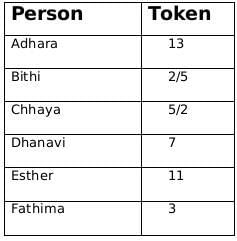
Adhara, Bithi, Chhaya, Dhanavi, Esther, and Fathima are the interviewers in a process that awards funding for new initiatives. Every interviewer individually interviews each of the candidates individually and awards a token only if she recommends funding. A token has a face value of 2, 3, 5, 7, 11, or 13. Each interviewer awards tokens of a single face value only. Once all six interviews are over for a candidate, the candidate receives a funding that is Rs.1000 times the product of the face values of all the tokens. For example, if a candidate has tokens with face values 2, 5, and 7, then they get a funding of Rs.1000 × (2 × 5 × 7) = Rs.70,000.
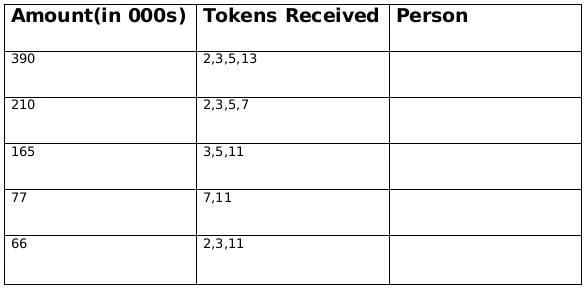
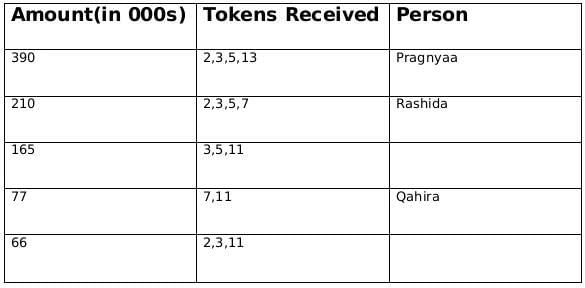
Pragnyaa, Qahira, Rasheeda, Smera, and Tantra were five candidates who received funding. The funds they received, in descending order, were Rs.390,000, Rs.210,000, Rs.165,000, Rs.77,000, and Rs.66,000.
The following additional facts are known:
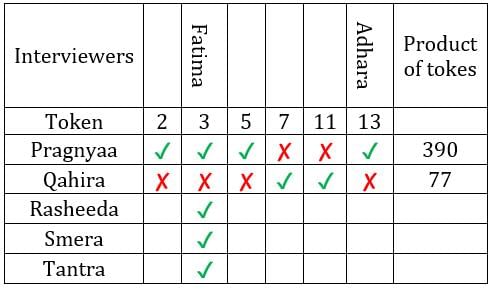
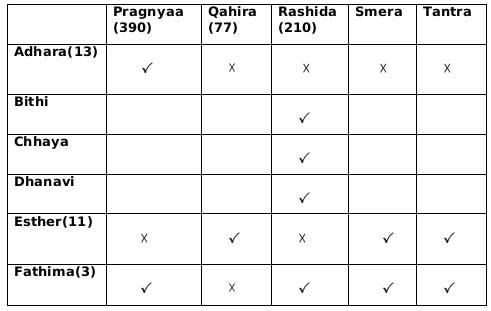
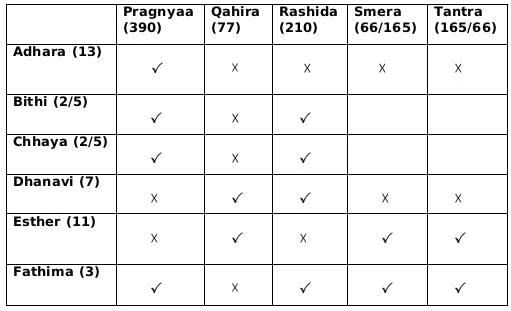
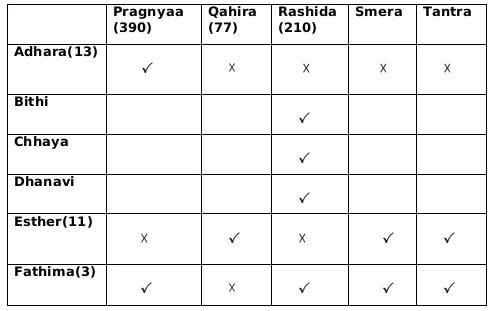
- Fathima awarded tokens to everyone except Qahira, while Adhara awarded tokens to no one except Pragnyaa.
- Rashida received the highest number of tokens that anyone received, but she did not receive one from Esther.
- Bithi awarded a token to Smera but not to Qahira, while Dhanavi awarded a token to Qahira but not to Smera.
Q1: How many tokens did Qahira receive?
Ans: 2
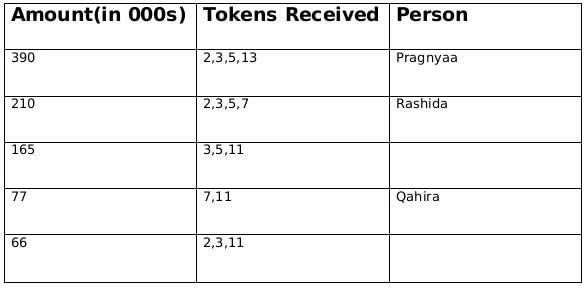
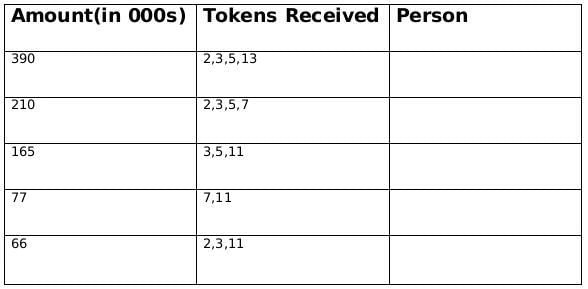
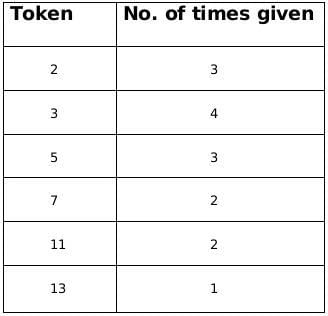
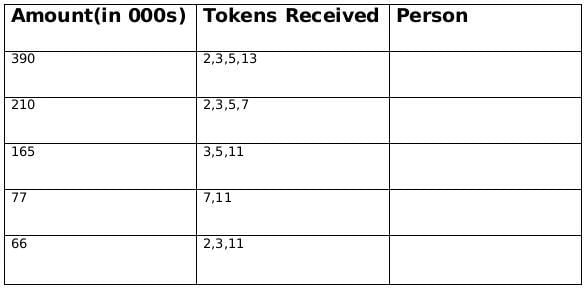
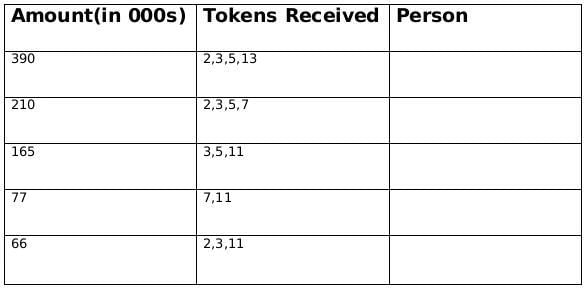
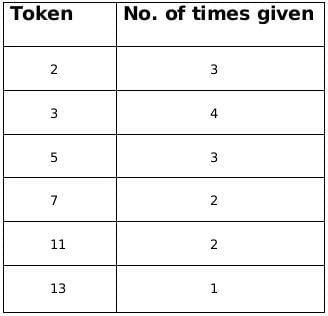
Sol: The funds they received, in descending order, were Rs.390,000, Rs.210,000, Rs.165,000, Rs.77,000, and Rs.66,000.
∴ The product of tokes = 390, 210, 165, 77, 66
⇒ Break of tokens received
390 = 2 × 3 × 5 × 13
210 = 2 × 3 × 5 × 7
165 = 3 × 5 × 11
77 = 7 × 11
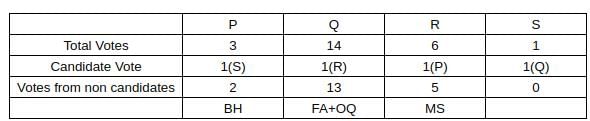
66 = 2 × 3 × 11
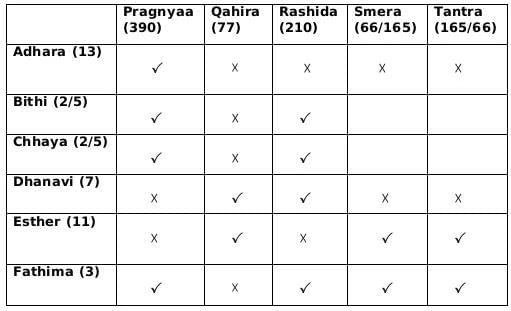
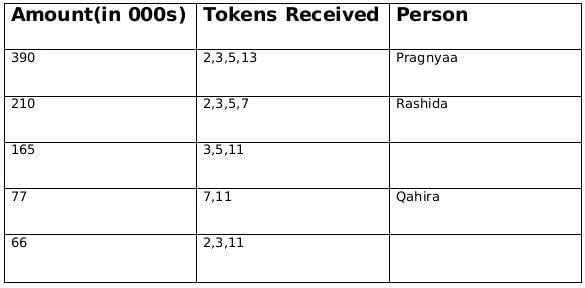
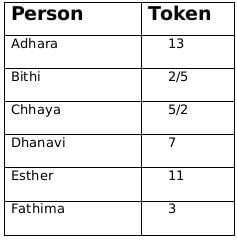
From (1): Fathima awarded tokens to everyone except Qahira,
∴ Fatima must have awarded token number 3 to everyone and Qahira received tokens whose product is 77.
From (1): Adhara awarded tokens to no one except Pragnyaa
∴ Adhara must have awared token 13 and Pragnyaa received tokens whose product is 390.
From (2): Rashida received the highest number of tokens that anyone received, but she did not receive one from Esther.
∴ Rashida must have received 4 tokes whose product can only be 210. Also, since Esther did not give her the token, hence Esther must have distributed token number 11.
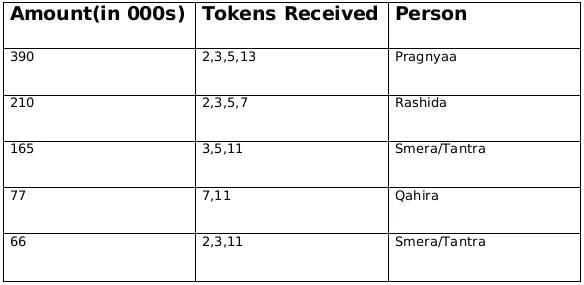
From (3): Dhanavi awarded a token to Qahira but not to Smera.
∴ Dhanavi must have awared token number 7.
From (3): Bithi awarded a token to Smera but not to Qahira
∴ Bithi/Chhaya could have awared token 2/5 in any order.
If Bithi gives token number 2 to S/T, then Chhaya will given token number 5 to T/S and vice-a-versa.
∴ Qahira received two tokens i.e., 7 and 11.
Q2: Who among the following definitely received a token from Bithi but not from Dhanavi?
(a) Qahira
(b) Tantra
(c) Pragnyaa
(d) Rasheeda
Ans: c
Sol:
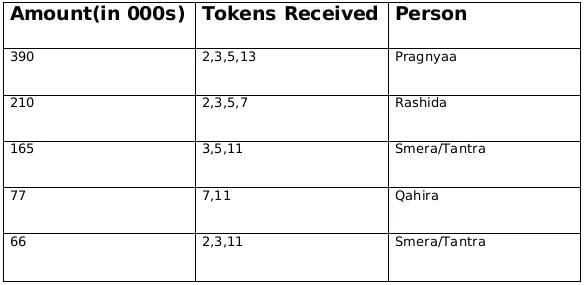
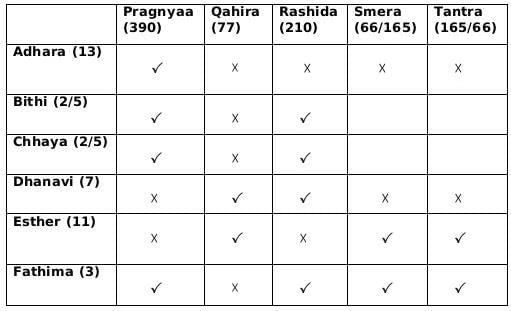
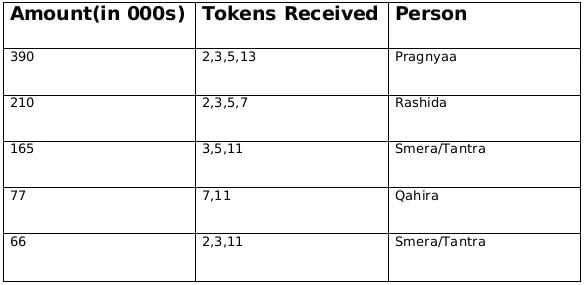
From statement 1 we can deduce that Fatima gave token 3 and Adhara gave token 13 and therefore from this we can say that Qahira received a funding of 77,000 and Pragnyaa received a funding of 390,000.
From statement 2, we know that Rashida received highest number of tokens and we already concluded that Pragnyaa received a funding of 390,000 so we can say that Rashida received a funding of 210,000.
Rashida did not received a token from Esther so we can also conclude that Esther gave the token number 11.
From statement 3 we can conclude that Dhanavi gave a token of 7, and Bethi Gave a token of either 2 or 5 and similarly Chhaya also gave a token of 2 or 5.
Alternate Explanation:
390=2×3×5×13
210=2×3×5×7
165=3×5×11
77=7×11
66=2×3×11
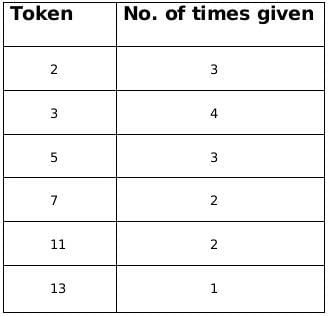
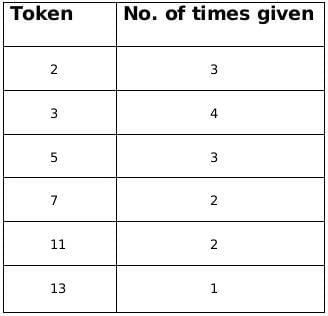
From the above information we can conclude that the number of times a particular token was given, therefore we get the following table,We know that there are five people who received the token and there are 6 people who awarded the token.
From, statement 1 we know that Fatima gave token to 4 people except Qahira so the token number given by Fatima is 3, and Adhara gave token only to Pragnyaa so the token number given by Adhara is 13. Therefore we can also say that Pragnyaa received 390,000 and Qahira received 77,000.
From statement 2, we know that Rashida received highest number of tokens and we already concluded that Pragnyaa received a funding of 390,000 so we can say that Rashida received a funding of 210,000. Rashida did not received a token from Esther so we can also conclude that Esther gave the token number 11.
From statement 3, we can conclude that Dhanavi gave a token of 7, and Bethi Gave a token of either 2 or 5 and similarly Chhaya also gave a token of 2 or 5.
Q3: How many tokens did Chhaya award?
Ans: 3
Sol:
From statement 1 we can deduce that Fatima gave token 3 and Adhara gave token 13 and therefore from this we can say that Qahira received a funding of 77,000 and Pragnyaa received a funding of 390,000.
From statement 2, we know that Rashida received highest number of tokens and we already concluded that Pragnyaa received a funding of 390,000 so we can say that Rashida received a funding of 210,000.
Rashida did not received a token from Esther so we can also conclude that Esther gave the token number 11.
From statement 3 we can conclude that Dhanavi gave a token of 7, and Bethi Gave a token of either 2 or 5 and similarly Chhaya also gave a token of 2 or 5.
Alternate Explanation:
390=2×3×5×13
210=2×3×5×7
165=3×5×11
77=7×11
66=2×3×11
From the above information we can conclude that the number of times a particular token was given, therefore we get the following table,We know that there are five people who received the token and there are 6 people who awarded the token.
From, statement 1 we know that Fatima gave token to 4 people except Qahira so the token number given by Fatima is 3, and Adhara gave token only to Pragnyaa so the token number given by Adhara is 13. Therefore we can also say that Pragnyaa received 390,000 and Qahira received 77,000.
From statement 2, we know that Rashida received highest number of tokens and we already concluded that Pragnyaa received a funding of 390,000 so we can say that Rashida received a funding of 210,000. Rashida did not received a token from Esther so we can also conclude that Esther gave the token number 11.
From statement 3, we can conclude that Dhanavi gave a token of 7, and Bethi Gave a token of either 2 or 5 and similarly Chhaya also gave a token of 2 or 5.
Q4: How many tokens did Smera receive?
Ans: 3
Sol:
From statement 1 we can deduce that Fatima gave token 3 and Adhara gave token 13 and therefore from this we can say that Qahira received a funding of 77,000 and Pragnyaa received a funding of 390,000.
From statement 2, we know that Rashida received highest number of tokens and we already concluded that Pragnyaa received a funding of 390,000 so we can say that Rashida received a funding of 210,000.
Rashida did not received a token from Esther so we can also conclude that Esther gave the token number 11.
From statement 3 we can conclude that Dhanavi gave a token of 7, and Bethi Gave a token of either 2 or 5 and similarly Chhaya also gave a token of 2 or 5.
Alternate Explanation:
390=2×3×5×13
210=2×3×5×7
165=3×5×11
77=7×11
66=2×3×11
From the above information we can conclude that the number of times a particular token was given, therefore we get the following table,We know that there are five people who received the token and there are 6 people who awarded the token.
From, statement 1 we know that Fatima gave token to 4 people except Qahira so the token number given by Fatima is 3, and Adhara gave token only to Pragnyaa so the token number given by Adhara is 13. Therefore we can also say that Pragnyaa received 390,000 and Qahira received 77,000.
From statement 2, we know that Rashida received highest number of tokens and we already concluded that Pragnyaa received a funding of 390,000 so we can say that Rashida received a funding of 210,000. Rashida did not received a token from Esther so we can also conclude that Esther gave the token number 11.
From statement 3, we can conclude that Dhanavi gave a token of 7, and Bethi Gave a token of either 2 or 5 and similarly Chhaya also gave a token of 2 or 5.
Q5: Which of the following could be the amount of funding that Tantra received?
(A) Rs. 66,000
(B) Rs. 165,000
(a) Both (A) and (B)
(b) Neither (A) nor (B)
(c) Only (A)
(d) Only (B)
Ans: a
Sol:
From statement 1 we can deduce that Fatima gave token 3 and Adhara gave token 13 and therefore from this we can say that Qahira received a funding of 77,000 and Pragnyaa received a funding of 390,000.
From statement 2, we know that Rashida received highest number of tokens and we already concluded that Pragnyaa received a funding of 390,000 so we can say that Rashida received a funding of 210,000.
Rashida did not received a token from Esther so we can also conclude that Esther gave the token number 11.
From statement 3 we can conclude that Dhanavi gave a token of 7, and Bethi Gave a token of either 2 or 5 and similarly Chhaya also gave a token of 2 or 5.
Alternate Explanation:
390=2×3×5×13
210=2×3×5×7
165=3×5×11
77=7×11
66=2×3×11
From the above information we can conclude that the number of times a particular token was given, therefore we get the following table,We know that there are five people who received the token and there are 6 people who awarded the token.
From, statement 1 we know that Fatima gave token to 4 people except Qahira so the token number given by Fatima is 3, and Adhara gave token only to Pragnyaa so the token number given by Adhara is 13. Therefore we can also say that Pragnyaa received 390,000 and Qahira received 77,000.
From statement 2, we know that Rashida received highest number of tokens and we already concluded that Pragnyaa received a funding of 390,000 so we can say that Rashida received a funding of 210,000. Rashida did not received a token from Esther so we can also conclude that Esther gave the token number 11.
From statement 3, we can conclude that Dhanavi gave a token of 7, and Bethi Gave a token of either 2 or 5 and similarly Chhaya also gave a token of 2 or 5.
Passage - 2
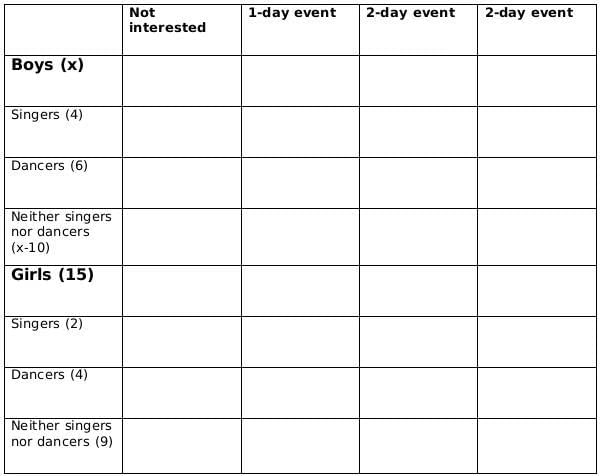
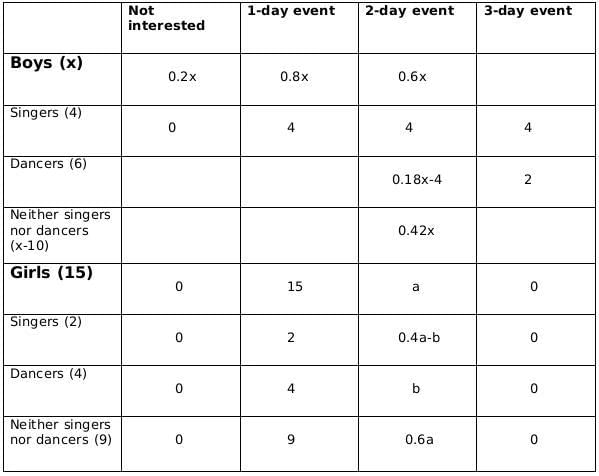
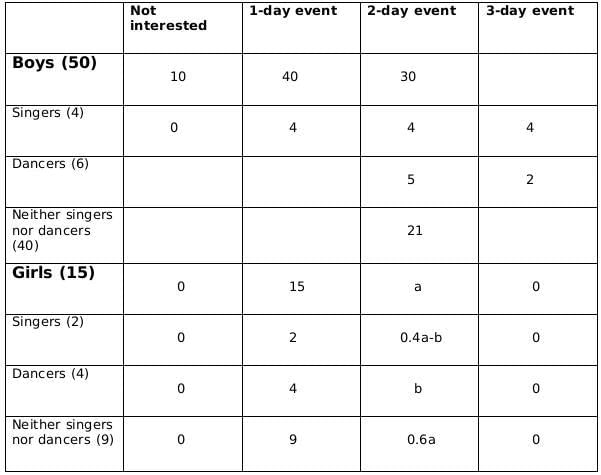
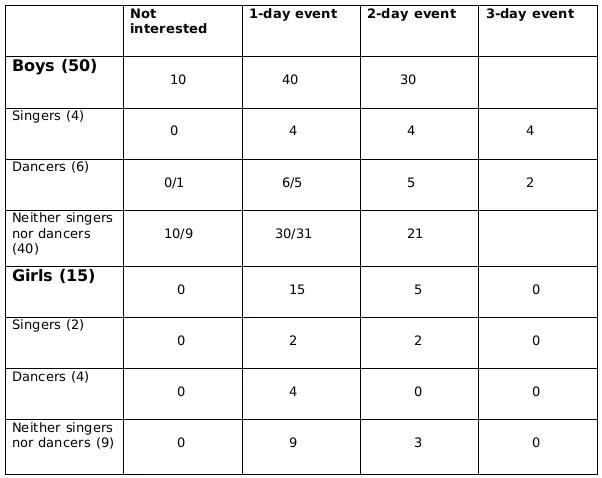
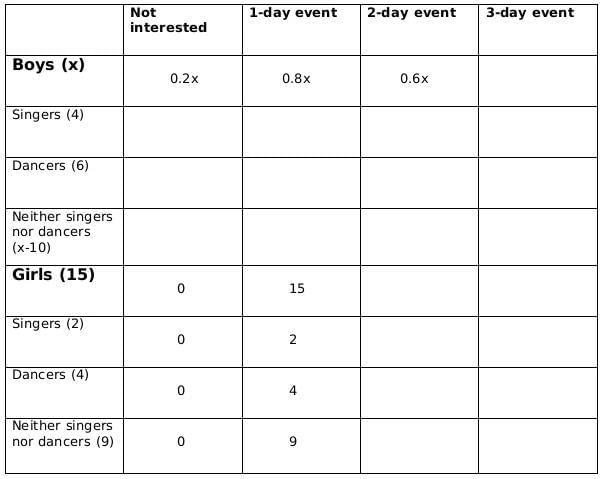
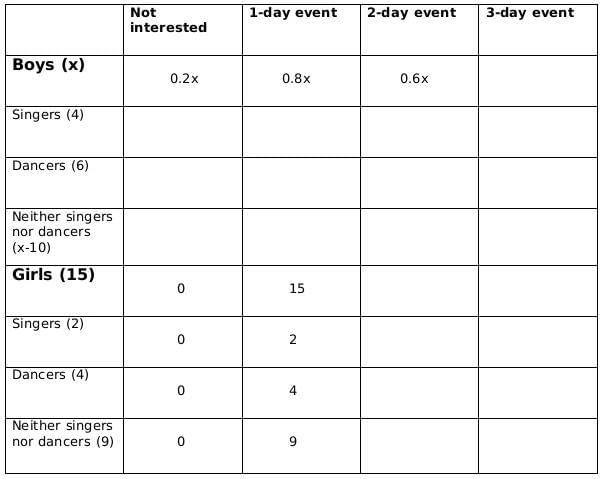
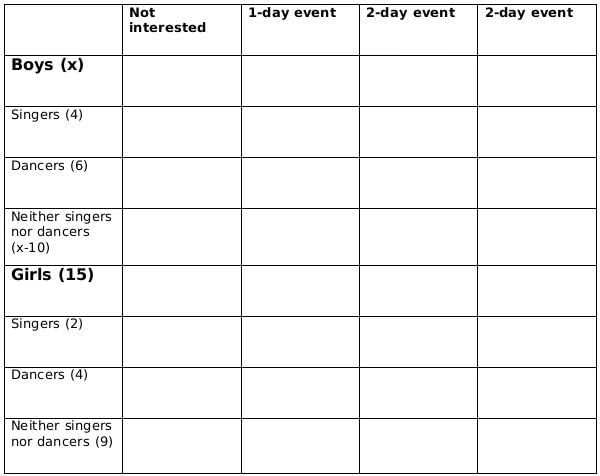
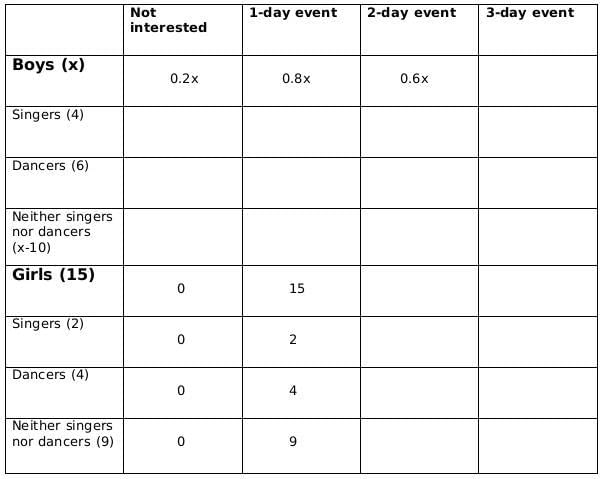
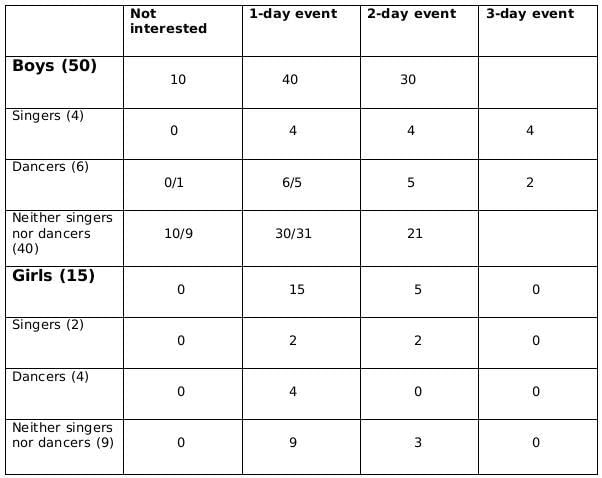
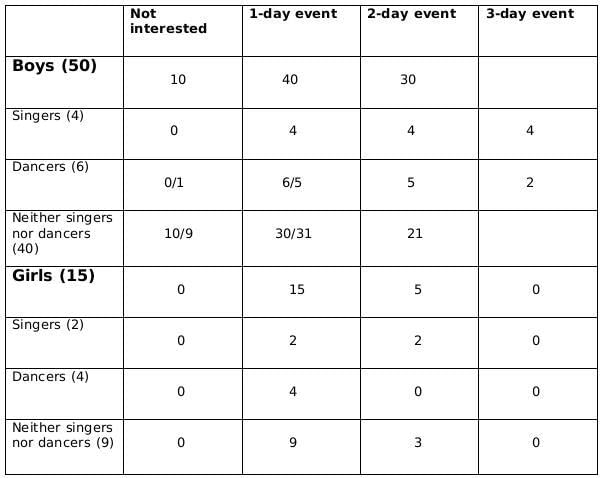
There are 15 girls and some boys among the graduating students in a class. They are planning a get-together, which can be either a 1-day event, or a 2-day event, or a 3-day event. There are 6 singers in the class, 4 of them are boys. There are 10 dancers in the class, 4 of them are girls. No dancer in the class is a singer.
Some students are not interested in attending the get-together. Those students who are interested in attending a 3-day event are also interested in attending a 2-day event; those who are interested in attending a 2-day event are also interested in attending a 1-day event.
The following facts are also known:
- Some of the girls are interested in attending a 1-day event, but not a 2-day event; some of the other girls are interested in attending both.
- 70% of the boys who are interested in attending a 2-day event are neither singers nor dancers. 60% of the girls who are interested in attending a 2-day event are neither singers nor dancers.
- No girl is interested in attending a 3-day event. All male singers and 2 of the dancers are interested in attending a 3-day event.
- The number of singers interested in attending a 2-day event is one more than the number of dancers interested in attending a 2-day event.
- All the girls and 80% of the boys are interested in attending a 1-day event. 60% of the boys are interested in attending a 2-day event.
Q1: How many boys are there in the class?
Ans: 50
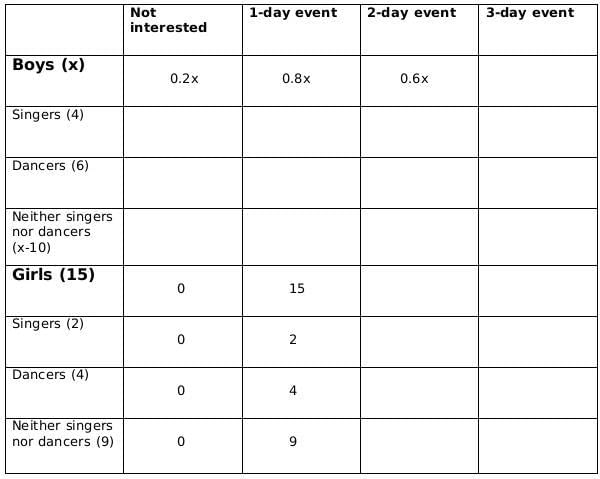
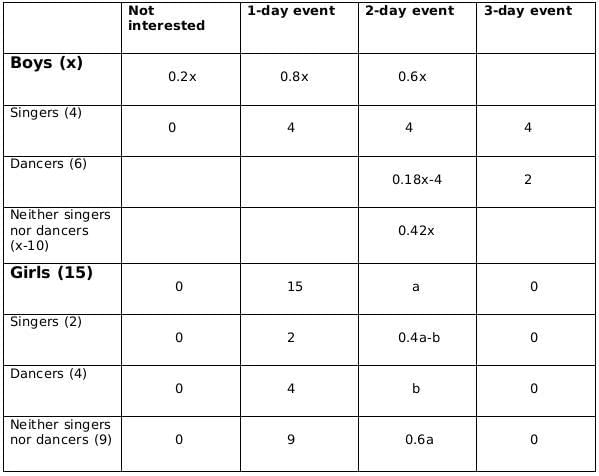
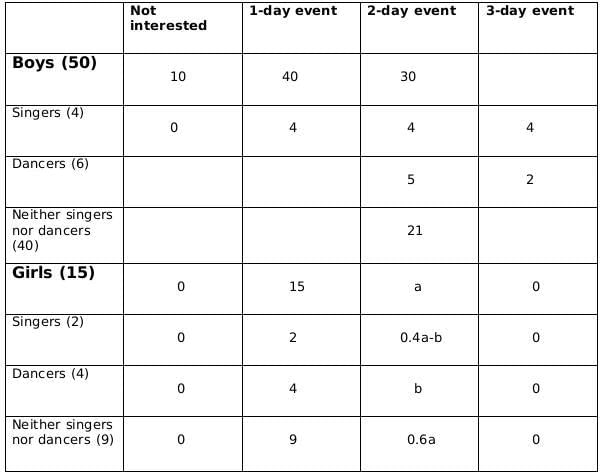
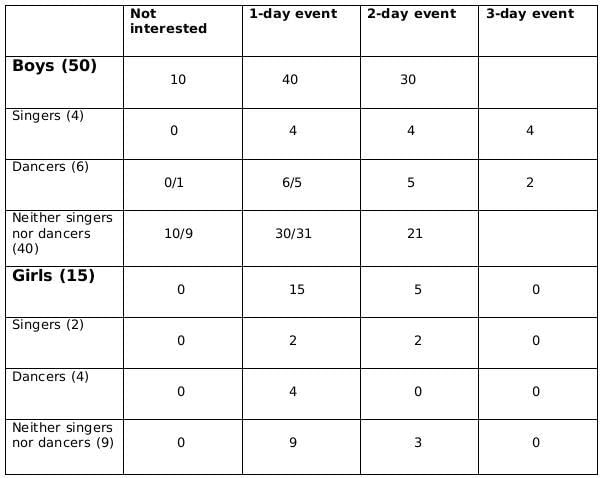
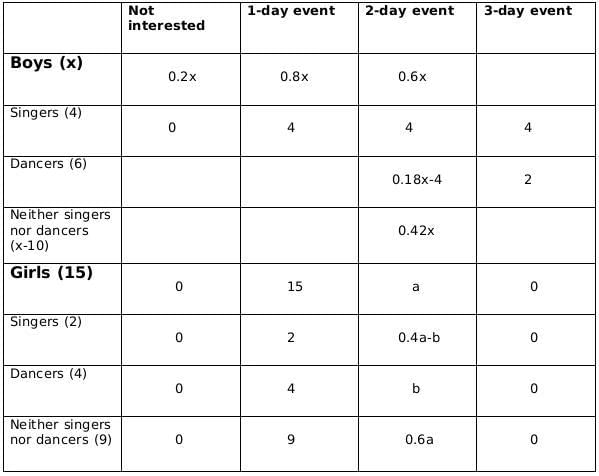
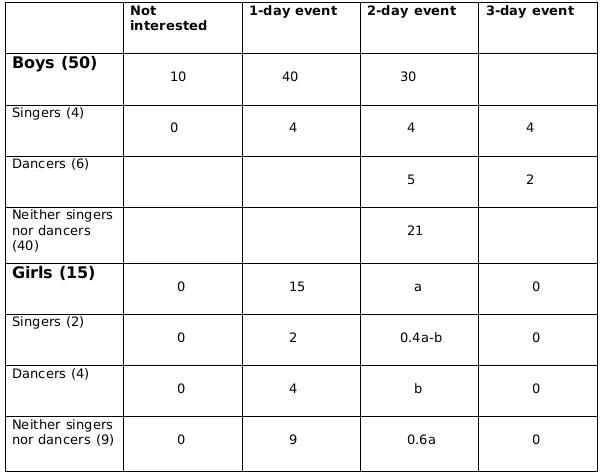
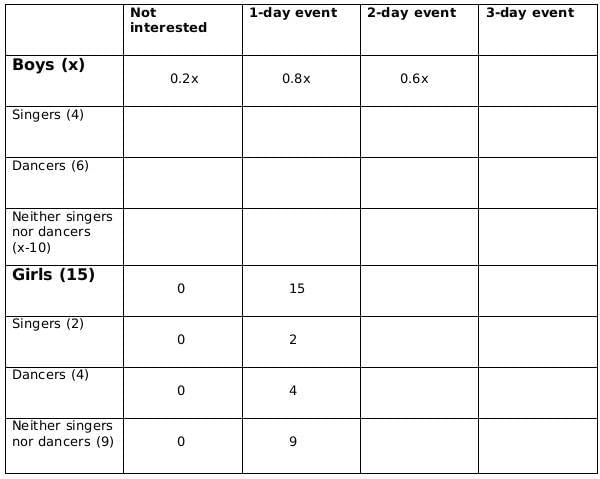
Sol: No. of girls = 15
Let the no. of boys be x
No. of singers = 6
No of boys who are singers = 4
Therefore, no of girls who are singers = 2
No of dancers = 10
No of boys who are dancers = 6
Therefore, no. of girls who are dancers = 4
No. of boys who are neither singers nor dancers = x-10
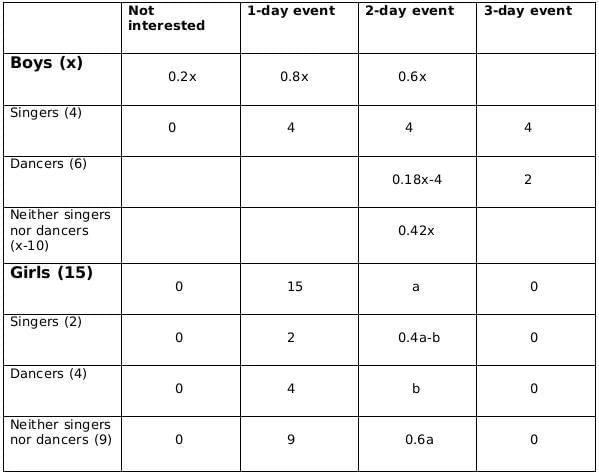
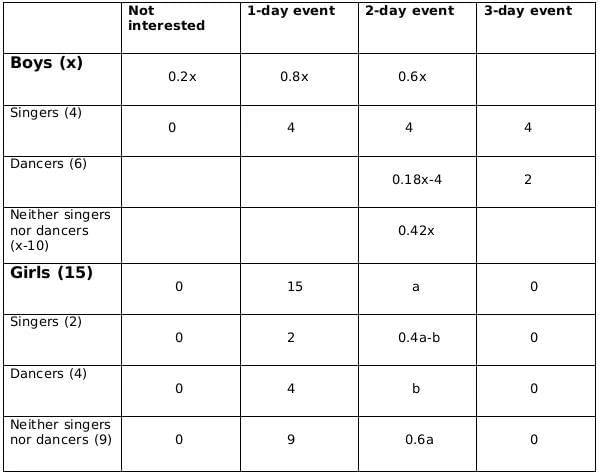
No. of girls who are neither singers nor dancers = 9Now we fill the above table, using statements 1 and 2, we get the following table
Let the number of girls who are interested in attending a 2-day event be a and the number of girls who are dancers and are interested in 2-day event be b.
Now using statements 3 and 4, we get2 ≤ 0.18x − 4 ≤ 6
6 ≤ 0.18x ≤ 10
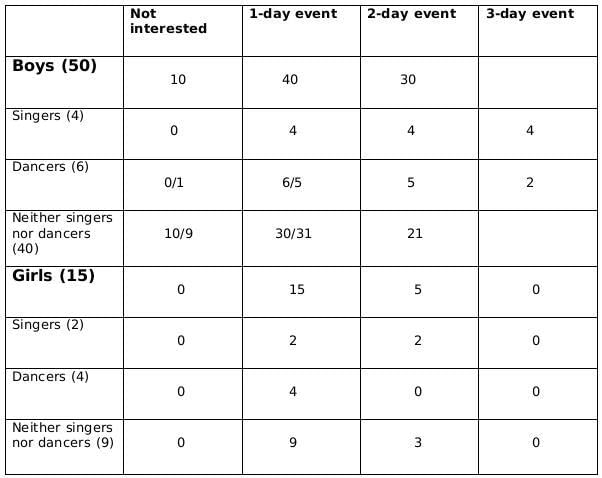
0.18x should be integer for which x should be a multiple of 50, and 0.18x lies between 6 and 10; therefore, the only possible value of x is 50.From statement 5, we can say that,
4+ 0.4a - b = 5+b +1
or, 0.4a = 2+2b
or, a = 5(1+b)
a should be a multiple of 5 as b is a whole number. So possible values of a can be 5, 10 or 15. Now, as the maximum value of b can be 4 and the maximum value of 0.4a-b can be 2, so the only possible value of a satisfying the conditions above is 5. If a= 5 then b=1.
Q2: Which of the following can be determined from the given information?
I. The number of boys who are interested in attending a 1-day event and are neither dancers nor singers.
II. The number of female dancers who are interested in attending a 1-day event.
(a) Only II
(b) Neither I nor II
(c) Both I and II
(d) Only I
Ans: a
Sol: No. of girls = 15
Let the no. of boys be x
No. of singers = 6
No of boys who are singers = 4
Therefore, no of girls who are singers = 2
No of dancers = 10
No of boys who are dancers = 6
Therefore, no. of girls who are dancers = 4
No. of boys who are neither singers nor dancers = x-10
No. of girls who are neither singers nor dancers = 9Now we fill the above table, using statements 1 and 2, we get the following table
Let the number of girls who are interested in attending a 2-day event be a and the number of girls who are dancers and are interested in 2-day event be b.
Now using statements 3 and 4, we get2 ≤ 0.18x − 4 ≤ 6
6 ≤ 0.18x ≤ 10
0.18x should be integer for which x should be a multiple of 50, and 0.18x lies between 6 and 10; therefore, the only possible value of x is 50.From statement 5, we can say that,
4+ 0.4a - b = 5+b +1
or, 0.4a = 2+2b
or, a = 5(1+b)
a should be a multiple of 5 as b is a whole number. So possible values of a can be 5, 10 or 15. Now, as the maximum value of b can be 4 and the maximum value of 0.4a-b can be 2, so the only possible value of a satisfying the conditions above is 5. If a= 5 then b=1.
Q3: What fraction of the class are interested in attending a 2-day event?
(a) 7/10
(b) 2/3
(c) 9/13
(d) 7/13
Ans: d
Sol: No. of girls = 15
Let the no. of boys be x
No. of singers = 6
No of boys who are singers = 4
Therefore, no of girls who are singers = 2
No of dancers = 10
No of boys who are dancers = 6
Therefore, no. of girls who are dancers = 4
No. of boys who are neither singers nor dancers = x-10
No. of girls who are neither singers nor dancers = 9Now we fill the above table, using statements 1 and 2, we get the following table
Let the number of girls who are interested in attending a 2-day event be a and the number of girls who are dancers and are interested in 2-day event be b.
Now using statements 3 and 4, we get2 ≤ 0.18x − 4 ≤ 6
6 ≤ 0.18x ≤ 10
0.18x should be integer for which x should be a multiple of 50, and 0.18x lies between 6 and 10; therefore, the only possible value of x is 50.From statement 5, we can say that,
4+ 0.4a - b = 5+b +1
or, 0.4a = 2+2b
or, a = 5(1+b)
a should be a multiple of 5 as b is a whole number. So possible values of a can be 5, 10 or 15. Now, as the maximum value of b can be 4 and the maximum value of 0.4a-b can be 2, so the only possible value of a satisfying the conditions above is 5. If a= 5 then b=1.Total students interested in 2-day event = 30+5 = 35
Total students = 15 + 50 = 65
Fraction = 35 = 7/13
Q4: What BEST can be concluded about the number of male dancers who are interested in attending a 1-day event?
(a) 4 or 6
(b) 6
(c) 5 or 6
(d) 5
Ans: c
Sol: No. of girls = 15
Let the no. of boys be x
No. of singers = 6
No of boys who are singers = 4
Therefore, no of girls who are singers = 2
No of dancers = 10
No of boys who are dancers = 6
Therefore, no. of girls who are dancers = 4
No. of boys who are neither singers nor dancers = x-10
No. of girls who are neither singers nor dancers = 9Now we fill the above table, using statements 1 and 2, we get the following table
Let the number of girls who are interested in attending a 2-day event be a and the number of girls who are dancers and are interested in 2-day event be b.
Now using statements 3 and 4, we get2 ≤ 0.18x − 4 ≤ 6
6 ≤ 0.18x ≤ 10
0.18x should be integer for which x should be a multiple of 50, and 0.18x lies between 6 and 10; therefore, the only possible value of x is 50.From statement 5, we can say that,
4+ 0.4a - b = 5+b +1
or, 0.4a = 2+2b
or, a = 5(1+b)
a should be a multiple of 5 as b is a whole number. So possible values of a can be 5, 10 or 15. Now, as the maximum value of b can be 4 and the maximum value of 0.4a-b can be 2, so the only possible value of a satisfying the conditions above is 5. If a= 5 then b=1.
Q5: How many female dancers are interested in attending a 2-day event?
(a) 1
(b) Cannot be determined
(c) 2
(d) 0
Ans: d
Sol: No. of girls = 15
Let the no. of boys be x
No. of singers = 6
No of boys who are singers = 4
Therefore, no of girls who are singers = 2
No of dancers = 10
No of boys who are dancers = 6
Therefore, no. of girls who are dancers = 4
No. of boys who are neither singers nor dancers = x-10
No. of girls who are neither singers nor dancers = 9Now we fill the above table, using statements 1 and 2, we get the following table
Let the number of girls who are interested in attending a 2-day event be a and the number of girls who are dancers and are interested in 2-day event be b.
Now using statements 3 and 4, we get2 ≤ 0.18x − 4 ≤ 6
6 ≤ 0.18x ≤ 10
0.18x should be integer for which x should be a multiple of 50, and 0.18x lies between 6 and 10; therefore, the only possible value of x is 50.From statement 5, we can say that,
4+ 0.4a - b = 5+b +1
or, 0.4a = 2+2b
or, a = 5(1+b)
a should be a multiple of 5 as b is a whole number. So possible values of a can be 5, 10 or 15. Now, as the maximum value of b can be 4 and the maximum value of 0.4a-b can be 2, so the only possible value of a satisfying the conditions above is 5. If a= 5 then b=1.
2021
Passage - 1
A journal plans to publish 18 research papers, written by eight authors (A, B, C, D, E, F, G, and H) in four issues of the journal scheduled in January, April, July and October. Each of the research papers was written by exactly one of the eight authors. Five papers were scheduled in each of the first two issues, while four were scheduled in each of the last two issues. Every author wrote at least one paper and at most three papers. The total number of papers written by A, D, G and H was double the total number of papers written by the other four authors.
Four of the authors were from India and two each were from Japan and China. Each author belonged to exactly one of the three areas — Manufacturing, Automation, and Logistics. Four of the authors were from the Logistics area and two were from the Automation area. As per the journal policy, none of the authors could have more than one paper in any issue of the journal.
The following facts are also known.
- A was from the Automation area and did not have a paper scheduled in the October issue.
- None of the Indian authors were from the Manufacturing area and none of the Japanese or Chinese authors were from the Automation area.
- A and H were from different countries, but had their papers scheduled in exactly the same issues.
- C and E, both Chinese authors from different areas, had the same number of papers scheduled. Further, E had papers scheduled in consecutive issues of the journal but C did not.
- B, from the Logistics area, had a paper scheduled in the April issue of the journal.
- B and G belonged to the same country. None of their papers were scheduled in the same issue of the journal.
- D, a Japanese author from the Manufacturing area, did not have a paper scheduled in the July issue.
- C and H belonged to different areas.
- F, an Indian author from the Logistics area, wrote only one paper. It was scheduled in the October issue.
Q1: What is the correct sequence of number of papers written by B, C, E and G, respectively?
(a) 1, 2, 2, 3
(b) 1, 3, 3, 1
(c) 3, 1, 1, 3
(d) 1, 2, 2, 1
Ans: a
Sol: Number of papers written by B, C, E, and G are: 1, 2, 2, 3
Q2: How many papers were written by Indian authors?
Ans: 8
Sol: total of 3+1+1+3 = 8 papers
Q3: How many papers were written by Indian authors?
Ans: 8
Sol: total of 3+1+1+3 = 8 papers
Q4: Which of the following statement(s) MUST be true?
Statement A: Every issue had at least one paper by author(s) from each country.
Statement B: Every issue had at most two papers by author(s) from each area.
(a) Both the statements
(b) Only Statement B
(c) Only Statement A
(d) Neither of the statements
Ans: c
Sol: il has three authors from logistics. Hence false
Q5: Which of the following statements is FALSE?
(a) Every issue had at least one paper by author(s) from Automation area.
(b) Every issue had exactly one paper by a Chinese author.
(c) Every issue had exactly two papers by authors from Logistics area.
(d) Every issue had exactly two papers by Indian authors.
Ans: c
Sol: He issue of April there were three authors from logistics department.
Q6: Which of the following statements is FALSE?
(a) There were exactly two papers by authors from Manufacturing area in the January issue.
(b) There was exactly one paper by an author from Manufacturing area in the April issue.
(c) There was exactly one paper by an author from Logistics area in the October issue.
(d) There were exactly two papers by authors from Manufacturing area in the July issue.
Ans: d
Sol: In the information, it is provided that there are four authors in the logistics department, 2 authors in automation, and 2 authors in manufacturing. There are 4 Indian authors, 2 Chinese authors, and 2 Japanese authors.
The total issues publicized were 18 of which the publications done by A, D, G, H are twice the papers written by the other four authors.
Hence A+D+G+H has written 12 papers in total and B+C+E+F has written 6 in total. Since an author can write a minimum of 4 papers and a maximum of 3 papers. Each of A, D, G, H must have written 3 papers each.
In statement 3 it was provided that none of the Indian authors were from the Manufacturing area and none of the Japanese or Chinese authors were from the Automation area.
Since none of the Japanese and Chinese authors belonged to automation. Hence the two automation authors must be from India. In statement 1 it was given that F an Indian author is from logistics.
Of the remaining 5 authors 3 from logistics and 2 from manufacturing, in statement 5 it is given that the two Chinese authors are from different areas and hence they must be from manufacturing and logistics.
Of the remaining 3 authors 2 in logistics and 1 in manufacturing, in statement 8 is given that a Japanese author belonged to manufacturing, and hence of the remaining 2 in logistics one of them was from India and the other from Japan.
Of the four Indian authors, 2 belonged to logistics and 2 automation. Of the two authors from Japan, one belonged to manufacturing and one logistics. Of the two Chinese authors, one of them belonged to logistics and the other manufacturing.
Five papers were scheduled in each of the January and April issues, while four were scheduled in each of July and October issues.
Using statement 1, F an Indian author wrote a single paper in logistics published in October.
Using statement 2, A was from Automation and did not have a paper scheduled in October. Since A wrote 3 papers in total he must have written in the other three months and since only Indian authors worked in Automation he must have been from India.
Using statement 5, C, E are Chinese and wrote an equal number of papers. Since B+C+E+F have written a total of 6 papers. The two possibilities are 2+2+1+1 or 3+1+1+1.. Since it was given that E had papers scheduled in consecutive issues and C did not. So the only possible case is C = 2, E =2, F = 1, B = 1.
Using statement 4, A and H were from different countries and wrote papers in the same months. Hence H must be Japanese and must have written in Jan, April, July.In statement 6, B, from the Logistics area, had a paper scheduled in the April issue of the journal.In statement 7, B and G belonged to the same country. None of their papers were scheduled in the same issue of the journal. Since B and G belonged to the same country the only possibility is that both of them belonged to the same country and since they published Journals in different months. G must have published in January, July, and October.
In statement 8, D, a Japanese author from the Manufacturing area, did not have a paper scheduled in the July issue. Hence he must have had the three issues in Jan, April, Oct. The other Japanese author H must have written in logistics.
The fourth Indian author G must have written a paper in Automation.
In January, one more paper needs to be publicized, one in April, 1 in July, and one in October.
In statement 5, E had papers scheduled in consecutive issues of the journal but C did not.
Hence C must have written in Jan and October, and E in April and July.
In statement 9, C and H belonged to different areas. Hence C must be from Manufacturing and E must be from Logistics.There are no authors from Manufacturing in the July issue and hence option D is false.
Q7: Which of the following is the correct sequence of number of papers by authors from Automation, Manufacturing and Logistics areas, respectively?
(a) 6, 5, 7
(b) 6, 6, 6
(c) 6, 7, 5
(d) 5, 6, 7
Ans: a
Sol: In the information, it is provided that there are four authors in the logistics department, 2 authors in automation, and 2 authors in manufacturing. There are 4 Indian authors, 2 Chinese authors, and 2 Japanese authors.
The total issues publicized were 18 of which the publications done by A, D, G, H are twice the papers written by the other four authors.
Hence A+D+G+H has written 12 papers in total and B+C+E+F has written 6 in total. Since an author can write a minimum of 4 papers and a maximum of 3 papers. Each of A, D, G, H must have written 3 papers each.
In statement 3 it was provided that none of the Indian authors were from the Manufacturing area and none of the Japanese or Chinese authors were from the Automation area.
Since none of the Japanese and Chinese authors belonged to automation. Hence the two automation authors must be from India. In statement 1 it was given that F an Indian author is from logistics.
Of the remaining 5 authors 3 from logistics and 2 from manufacturing, in statement 5 it is given that the two Chinese authors are from different areas and hence they must be from manufacturing and logistics.
Of the remaining 3 authors 2 in logistics and 1 in manufacturing, in statement 8 is given that a Japanese author belonged to manufacturing, and hence of the remaining 2 in logistics one of them was from India and the other from Japan.
Of the four Indian authors, 2 belonged to logistics and 2 automation. Of the two authors from Japan, one belonged to manufacturing and one logistics. Of the two Chinese authors, one of them belonged to logistics and the other manufacturing.
Five papers were scheduled in each of the January and April issues, while four were scheduled in each of July and October issues.
Using statement 1, F an Indian author wrote a single paper in logistics published in October.
Using statement 2, A was from Automation and did not have a paper scheduled in October. Since A wrote 3 papers in total he must have written in the other three months and since only Indian authors worked in Automation he must have been from India.
Using statement 5, C, E are Chinese and wrote an equal number of papers. Since B+C+E+F have written a total of 6 papers. The two possibilities are 2+2+1+1 or 3+1+1+1.. Since it was given that E had papers scheduled in consecutive issues and C did not. So the only possible case is C = 2, E =2, F = 1, B = 1.
Using statement 4, A and H were from different countries and wrote papers in the same months. Hence H must be Japanese and must have written in Jan, April, July.In statement 6, B, from the Logistics area, had a paper scheduled in the April issue of the journal.In statement 7, B and G belonged to the same country. None of their papers were scheduled in the same issue of the journal. Since B and G belonged to the same country the only possibility is that both of them belonged to the same country and since they published Journals in different months. G must have published in January, July, and October.
In statement 8, D, a Japanese author from the Manufacturing area, did not have a paper scheduled in the July issue. Hence he must have had the three issues in Jan, April, Oct. The other Japanese author H must have written in logistics.
The fourth Indian author G must have written a paper in Automation.
In January, one more paper needs to be publicized, one in April, 1 in July, and one in October.
In statement 5, E had papers scheduled in consecutive issues of the journal but C did not.
Hence C must have written in Jan and October, and E in April and July.
In statement 9, C and H belonged to different areas. Hence C must be from Manufacturing and E must be from Logistics.In Automation, there are a total of 6 papers, Logistics 7 papers, and Manufacturing a total of 5 papers.
Passage - 2
Ten objects o1, o2, …, o10 were distributed among Amar, Barat, Charles, Disha, and Elise. Each item went to exactly one person. Each person got exactly two of the items, and this pair of objects is called her/his bundle.
The following table shows how each person values each object.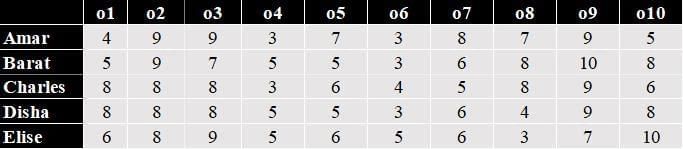
The value of any bundle by a person is the sum of that person’s values of the objects in that bundle. A person X envies another person Y if X values Y’s bundle more than X’s own bundle.
For example, hypothetically suppose Amar’s bundle consists of o1 and o2, and Barat’s bundle consists of o3 and o4. Then Amar values his own bundle at 4 + 9 = 13 and Barat’s bundle at 9 + 3 = 12. Hence Amar does not envy Barat. On the other hand, Barat values his own bundle at 7 + 5 = 12 and Amar’s bundle at 5 + 9 = 14. Hence Barat envies Amar.
The following facts are known about the actual distribution of the objects among the five people.
- Objects o1, o2, and o3 were given to three different people.
- Objects o1 and o8 were given to different people.
- Three people value their own bundles at 16. No one values her/his own bundle at a number higher than 16.
- Disha values her own bundle at an odd number. All others value their own bundles at an even number.
- Some people who value their own bundles less than 16 envy some other people who value their own bundle at 16. No one else envies others.
- If someone’s value for an object is 10, then she/he received that object.
Q1: What BEST can be said about object o8?
(a) o8 was given to Amar, Charles, or Disha
(b) o8 was given to Disha
(c) o8 was given to Charles
(d) o8 was given to Charles or Disha
Ans: c
Sol: We have the following table:o10 is given to Elise and o9 is given to Bharat .
Now as Elise values his own bundle at an even number so the only two objects which can be given to Elise is o1 or o5 or o7.
Case 1: o1 is given to Elise Now the total valuation of Elise = 12 Valuation of Disha is an odd number So we can say Amar , Bharat and Charles values their bundles at 16.
So for Bharat the valuation to be 16, o7 will be given to him so we get Bharat - o9 and o7 and Elise -o10 and o1 For charles to have valuation 16 the only way = 8+8 so we can say o8 is given to charles along with either o2 or o3 .(o1 and o8 cannot be together ) Now for Amart to have a valuation of 16 the only way possible = 9+7 Now so we can say Amar will receive either o2 or o3 and o5 .
Now we are left with 04 and o6 So if Disha receives o4 and o6 The valuation of Disha will be 5+3 =8 which is not an odd number so this case is discarded.
Case 2: Elise receives o5 or o7.
Now Valuation of Elise = 16 .
And Elise receives o10 and o5/o7.
Bharat received o9 and we know the evaluation of Bharat is an even number and the minimum even number possible for valuation of Bharat is 16 and no one can have evaluation more than 16 so Bharat received o7 .
So Elise received o5.
So we have Bharat - o9 ,o7 Elise -o10,o5.
Now as we know o1 ,o2 and o3 are given to three different persons so they are Amar, Charles and Disha . Now As per Amar he values Bharat at 17 so he envy him So Amar will value his bundle less than 16 So the only possibility for Amar to value his bundle less than 16 = 12 =9+3.
Now we can say Charu will have 16 as his own valuation so he will get 8+8 . Now o8 will be given to Charu, and he cannot have o1 , also he cannot have o2 because if he has o2 he will value Bharat’s bundle as 17 and will envy him which is not possible so Charu will have o3,o8 Now Amar will have o2 and Disha will have o1.
Now Amar will not have o4 because in that case Charles will envy Amar and is not possible so we can say Amar will have o6 and Disha will have o4.
So we have the following :
Amar - o2,o6
Bharat -o9,o7
Charu -o3,o8
Disha o1,o4
Elise -o10,o5
So o8 is given to Charu.
Q2: Who among the following envies someone else?
(a) Barat
(b) Charles
(c) Amar
(d) Elise
Ans: c
Sol: We have the following table :o10 is given to Elise and o9 is given to Bharat .
Now as Elise values his own bundle at an even number so the only two objects which can be given to Elise is o1 or o5 or o7.
Case 1: o1 is given to Elise Now the total valuation of Elise = 12 Valuation of Disha is an odd number So we can say Amar , Bharat and Charles values their bundles at 16 .
So for Bharat the valuation to be 16, o7 will be given to him so we get Bharat - o9 and o7 and Elise -o10 and o1 For charles to have valuation 16 the only way = 8+8 so we can say o8 is given to charles along with either o2 or o3 .(o1 and o8 cannot be together ) Now for Amart to have a valuation of 16 the only way possible = 9+7 Now so we can say Amar will receive either o2 or o3 and o5 .
Now we are left with 04 and o6 So if Disha receives o4 and o6 The valuation of Disha will be 5+3 =8 which is not an odd number so this case is discarded.
Case 2: Elise receives o5 or o7 .
Now Valuation of Elise = 16 .
And Elise receives o10 and o5/o7.
Bharat received o9 and we know the evaluation of Bharat is an even number and the minimum even number possible for valuation of Bharat is 16 and no one can have evaluation more than 16 so Bharat received o7 .
So Elise received o5 .
So we have Bharat - o9 ,o7 Elise -o10,o5.
Now as we know o1 ,o2 and o3 are given to three different persons so they are Amar, Charles and Disha . Now As per Amar he values Bharat at 17 so he envy him So Amar will value his bundle less than 16 So the only possibility for Amar to value his bundle less than 16 = 12 =9+3.
Now we can say Charu will have 16 as his own valuation so he will get 8+8 . Now o8 will be given to Charu, and he cannot have o1 , also he cannot have o2 because if he has o2 he will value Bharat’s bundle as 17 and will envy him which is not possible so Charu will have o3,o8 Now Amar will have o2 and Disha will have o1.
Now Amar will not have o4 because in that case Charles will envy Amar and is not possible so we can say Amar will have o6 and Disha will have o4.
So we have the following :
Amar - o2,o6
Bharat -o9,o7
Charu -o3,o8
Disha o1,o4
Elise -o10,o5
So Amar envies someone else
Q3: What is Amar’s value for his own bundle?
Ans: 12
Sol: We have the following table :o10 is given to Elise and o9 is given to Bharat .
Now as Elise values his own bundle at an even number so the only two objects which can be given to Elise is o1 or o5 or o7.
Case 1 : o1 is given to Elise Now the total valuation of Elise = 12 Valuation of Disha is an odd number So we can say Amar , Bharat and Charles values their bundles at 16 .
So for Bharat the valuation to be 16, o7 will be given to him so we get Bharat - o9 and o7 and Elise -o10 and o1 For charles to have valuation 16 the only way = 8+8 so we can say o8 is given to charles along with either o2 or o3 .(o1 and o8 cannot be together ) Now for Amart to have a valuation of 16 the only way possible = 9+7 Now so we can say Amar will receive either o2 or o3 and o5 .
Now we are left with 04 and o6 So if Disha receives o4 and o6 The valuation of Disha will be 5+3 =8 which is not an odd number so this case is discarded.
Case 2 Elise receives o5 or o7.
Now Valuation of Elise = 16 .
And Elise receives o10 and o5/o7.
Bharat received o9 and we know the evaluation of Bharat is an even number and the minimum even number possible for valuation of Bharat is 16 and no one can have evaluation more than 16 so Bharat received o7 .
So Elise received o5.
So we have Bharat - o9 ,o7 Elise -o10,o5.
Now as we know o1 ,o2 and o3 are given to three different persons so they are Amar, Charles and Disha . Now As per Amar he values Bharat at 17 so he envy him So Amar will value his bundle less than 16 So the only possibility for Amar to value his bundle less than 16 = 12 =9+3.
Now we can say Charu will have 16 as his own valuation so he will get 8+8 . Now o8 will be given to Charu, and he cannot have o1 , also he cannot have o2 because if he has o2 he will value Bharat’s bundle as 17 and will envy him which is not possible so Charu will have o3,o8 Now Amar will have o2 and Disha will have o1.
Now Amar will not have o4 because in that case Charles will envy Amar and is not possible so we can say Amar will have o6 and Disha will have o4.
So we have the following :
Amar - o2,o6
Bharat -o9,o7
Charu -o3,o8
Disha o1,o4
Elise -o10,o5
Amar's own valuation = 9+3 =12
Q4: Object o4 was given to
(a) Elise
(b) Barat
(c) Charles
(d) Disha
Ans: d
Sol: We have the following table :o10 is given to Elise and o9 is given to Bharat .
Now as Elise values his own bundle at an even number so the only two objects which can be given to Elise is o1 or o5 or o7.
Case 1 : o1 is given to Elise Now the total valuation of Elise = 12 Valuation of Disha is an odd number So we can say Amar, Bharat and Charles values their bundles at 16.
So for Bharat the valuation to be 16, o7 will be given to him so we get Bharat - o9 and o7 and Elise -o10 and o1 For charles to have valuation 16 the only way = 8+8 so we can say o8 is given to charles along with either o2 or o3 .(o1 and o8 cannot be together ) Now for Amart to have a valuation of 16 the only way possible = 9+7 Now so we can say Amar will receive either o2 or o3 and o5 .
Now we are left with 04 and o6 So if Disha receives o4 and o6 The valuation of Disha will be 5+3 =8 which is not an odd number so this case is discarded.
Case 2 Elise receives o5 or o7.
Now Valuation of Elise = 16 .
And Elise receives o10 and o5/o7.
Bharat received o9 and we know the evaluation of Bharat is an even number and the minimum even number possible for valuation of Bharat is 16 and no one can have evaluation more than 16 so Bharat received o7 .
So Elise received o5.
So we have Bharat - o9 ,o7 Elise -o10,o5.
Now as we know o1 ,o2 and o3 are given to three different persons so they are Amar, Charles and Disha . Now As per Amar he values Bharat at 17 so he envy him So Amar will value his bundle less than 16 So the only possibility for Amar to value his bundle less than 16 = 12 =9+3.
Now we can say Charu will have 16 as his own valuation so he will get 8+8 . Now o8 will be given to Charu, and he cannot have o1 , also he cannot have o2 because if he has o2 he will value Bharat’s bundle as 17 and will envy him which is not possible so Charu will have o3,o8 Now Amar will have o2 and Disha will have o1.
Now Amar will not have o4 because in that case Charles will envy Amar and is not possible so we can say Amar will have o6 and Disha will have o4.
So we have the following :
Amar - o2,o6
Bharat -o9,o7
Charu -o3,o8
Disha o1,o4
Elise -o10,o5
o4 is given to Disha
Q5: Object o5 was given to
(a) Disha
(b) Elise
(c) Amar
(d) Charles
Ans: b
Sol: We have the following table :o10 is given to Elise and o9 is given to Bharat .
Now as Elise values his own bundle at an even number so the only two objects which can be given to Elise is o1 or o5 or o7.
Case 1 : o1 is given to Elise Now the total valuation of Elise = 12 Valuation of Disha is an odd number So we can say Amar , Bharat and Charles values their bundles at 16 .
So for Bharat the valuation to be 16, o7 will be given to him so we get Bharat - o9 and o7 and Elise -o10 and o1 For charles to have valuation 16 the only way = 8+8 so we can say o8 is given to charles along with either o2 or o3 .(o1 and o8 cannot be together ) Now for Amart to have a valuation of 16 the only way possible = 9+7 Now so we can say Amar will receive either o2 or o3 and o5 .
Now we are left with 04 and o6 So if Disha receives o4 and o6 The valuation of Disha will be 5+3 =8 which is not an odd number so this case is discarded.
Case 2 Elise receives o5 or o7.
Now Valuation of Elise = 16.
And Elise receives o10 and o5/o7.
Bharat received o9 and we know the evaluation of Bharat is an even number and the minimum even number possible for valuation of Bharat is 16 and no one can have evaluation more than 16 so Bharat received o7 .
So Elise received o5.
So we have Bharat - o9 ,o7 Elise -o10,o5.
Now as we know o1 ,o2 and o3 are given to three different persons so they are Amar, Charles and Disha . Now As per Amar he values Bharat at 17 so he envy him So Amar will value his bundle less than 16 So the only possibility for Amar to value his bundle less than 16 = 12 =9+3.
Now we can say Charu will have 16 as his own valuation so he will get 8+8 . Now o8 will be given to Charu, and he cannot have o1 , also he cannot have o2 because if he has o2 he will value Bharat’s bundle as 17 and will envy him which is not possible so Charu will have o3,o8 Now Amar will have o2 and Disha will have o1.
Now Amar will not have o4 because in that case Charles will envy Amar and is not possible so we can say Amar will have o6 and Disha will have o4.
So we have the following :
Amar - o2,o6
Bharat -o9,o7
Charu -o3,o8
Disha o1,o4
Elise -o10,o5
o5 is given to Elise
Q6: What BEST can be said about the distribution of object o1?
(a) o1 was given to Disha
(b) o1 was given to Charles
(c) o1 was given to Charles, Disha, or Elise
(d) o1 was given to Charles or Disha
Ans: a
Sol: We have the following table :o10 is given to Elise and o9 is given to Bharat .
Now as Elise values his own bundle at an even number so the only two objects which can be given to Elise is o1 or o5 or o7.
Case 1 : o1 is given to Elise Now the total valuation of Elise = 12 Valuation of Disha is an odd number So we can say Amar , Bharat and Charles values their bundles at 16 .
So for Bharat the valuation to be 16, o7 will be given to him so we get Bharat - o9 and o7 and Elise -o10 and o1 For charles to have valuation 16 the only way = 8+8 so we can say o8 is given to charles along with either o2 or o3 .(o1 and o8 cannot be together ) Now for Amart to have a valuation of 16 the only way possible = 9+7 Now so we can say Amar will receive either o2 or o3 and o5 .
Now we are left with 04 and o6 So if Disha receives o4 and o6 The valuation of Disha will be 5+3 =8 which is not an odd number so this case is discarded.
Case 2 Elise receives o5 or o7 .
Now Valuation of Elise = 16 .
And Elise receives o10 and o5/o7.
Bharat received o9 and we know the evaluation of Bharat is an even number and the minimum even number possible for valuation of Bharat is 16 and no one can have evaluation more than 16 so Bharat received o7 .
So Elise received o5 .
So we have Bharat - o9 ,o7 Elise -o10,o5.
Now as we know o1 ,o2 and o3 are given to three different persons so they are Amar, Charles and Disha . Now As per Amar he values Bharat at 17 so he envy him So Amar will value his bundle less than 16 So the only possibility for Amar to value his bundle less than 16 = 12 =9+3.
Now we can say Charu will have 16 as his own valuation so he will get 8+8 . Now o8 will be given to Charu, and he cannot have o1 , also he cannot have o2 because if he has o2 he will value Bharat’s bundle as 17 and will envy him which is not possible so Charu will have o3,o8 Now Amar will have o2 and Disha will have o1.
Now Amar will not have o4 because in that case Charles will envy Amar and is not possible so we can say Amar will have o6 and Disha will have o4.
So we have the following :
Amar - o2,o6
Bharat -o9,o7
Charu -o3,o8
Disha o1,o4
Elise -o10,o5
So o1 is given to Disha
Passage - 3
Three reviewers Amal, Bimal, and Komal are tasked with selecting questions from a pool of 13 questions (Q01 to Q13). Questions can be created by external “subject matter experts” (SMEs) or by one of the three reviewers. Each of the reviewers either approves or disapproves a question that is shown to them. Their decisions lead to eventual acceptance or rejection of the question in the manner described below.
If a question is created by an SME, it is reviewed first by Amal, and then by Bimal. If both of them approve the question, then the question is accepted and is not reviewed by Komal. If both disapprove the question, it is rejected and is not reviewed by Komal. If one of them approves the question and the other disapproves it, then the question is reviewed by Komal. Then the question is accepted only if she approves it.
A question created by one of the reviewers is decided upon by the other two. If a question is created by Amal, then it is first reviewed by Bimal. If Bimal approves the question, then it is accepted. Otherwise, it is reviewed by Komal. The question is then accepted only if Komal approves it. A similar process is followed for questions created by Bimal, whose questions are first reviewed by Komal, and then by Amal only if Komal disapproves it. Questions created by Komal are first reviewed by Amal, and then, if required, by Bimal.
The following facts are known about the review process after its completion.
- Amal reviewed only Q02, Q03, Q04, Q06, Q08, Q10, Q11, and Q13.
- Bimal reviewed only Q02, Q04, Q06 through Q09, Q12, and Q13.
- Komal reviewed only Q01 through Q05, Q07, Q08, Q09, Q11, and Q12.
- Q02, Q06, Q09, Q11, and Q12 were rejected and the other questions were accepted.
Q1: How many questions were DEFINITELY created by Amal?
Ans: 3
Sol: Amal definitely prepared questions Q07, Q09, Q12.
Q2: How many questions were DEFINITELY created by Komal?
Ans: 1
Sol: Q10 was definitely prepared by Komal.
Q3: How many questions were DEFINITELY created by the SMEs?
Ans: 3
Sol: Q02, Q04, Q08 were prepared SME
Q4: How many questions were DEFINITELY disapproved by Bimal?
(a) 3
(b) 4
(c) 7
(d) 5
Ans: b
Sol: was rejected this has a possibility of being prepared by an external person and faced rejection by one among Amal and Bimal and Komal. (SME).
Q03-Was accepted and reviewed by Amal, Komal and hence must have been prepared by Bimal(Bimal).
Q04- Accepted and reviewed by the three of them and hence must have been prepared by an external expert. (SME).
Q05-Only reviewed by Komal and is accepted and hence must be prepared by Bimal. (Bimal)
Q06-Rejected and reviewed by Amal and Bimal. Hence could have been prepared by Komal or External and rejected by Bimal and Amal. (Komal/SME).
Q07-Accepted and reviewed by Bimal and Komal. Hence must have been prepared by Amal. (Amal).
Q08- Reviewed by Amal, Bimal, and Komal and is accepted. Hence must have been prepared by SME. (SME)
Q09- Reviewed by Bimal and Komal and is rejected. It must have been prepared by Amal and was rejected by both of them. (Amal).
Q10- Was reviewed by Amal and was accepted. Must have been prepared by Komal. (Komal)
Q11- Reviewed by Amal and Komal and was rejected. Must have been prepared by Bimal and rejected by both Amal and Komal. (Bimal)
Q12- Reviewed by Bimal and Komal and was rejected. Must have been prepared by Amal and was rejected by both Bimal and Komal. (Amal).
Q13- Reviewed by Amal and Bimal and was accepted. The question could have been prepared by Komal or SME. (Komal/SME).
Q06 irrespective of the question prepared by Komal/SME Bimal must reject the question.
Q07, Q09, Q12 are prepared by Amal and were reviewed by Bimal first and Komal next for this to happen Bimal must reject these questions.
Hence a total of four questions were rejected by Bimal.
Q5: The approval ratio of a reviewer is the ratio of the number of questions (s)he approved to the number of questions (s)he reviewed. Which option best describes Amal’s approval ratio?
(a) either 0.25 or 0.75
(b) 0.25
(c) lies between 0.25 and 0.50
(d) lies between 0.25 and 0.75
Ans: d
Sol: reviewed the questions:
Q02, Q03, Q04, Q06, Q08, Q10, Q11, and Q13.
For Q2 - Amal can either approve or reject the question.
For Q3- Amal must approve the question.
For Q4 -Amal can either approve or reject the question.
For Q06 - Amal must reject the question.
For Q08 - Amal can either approve or reject the question.
For Q10 - Amal must approve the question.
For Q11 - Amal must reject the question.
For Q13- Amal can either approve or reject the question.
The approval ratio has a minimum of 2 questions only Q3, Q10, and a maximum of 6 questions Q02, Q3, Q04, Q08, Q10, Q13.
Hence 2/8 = 0.25 to 6/8 = 0.75
Q6: How many questions created by Amal or Bimal were disapproved by at least one of the other reviewers?
(a) 7
(b) 4
(c) 5
(d) 2
Ans: c
Sol: could have possibly created the questions :
Q07, Q09, Q12 of which all three of them were reviewed by two people each, and hence they must have been rejected by the first reviewer.
Bimal could have created the questions : Q01, Q03, Q05, Q 11.
Q01, Q05 are reviewed only by Komal and hence did not have any rejection.
Q03, Q11 faced at least one rejection.
Hence a total of five questions.
|
77 videos|180 docs|96 tests
|
FAQs on CAT Previous Year Questions: Generic Puzzles - Logical Reasoning (LR) and Data Interpretation (DI)
| 1. What types of generic puzzles are commonly included in the CAT exam? |  |
| 2. How can I prepare for generic puzzles in the CAT exam? |  |
| 3. Are there specific strategies to solve generic puzzles quickly during the CAT exam? |  |
| 4. How important are generic puzzles in the overall CAT exam scoring? |  |
| 5. Where can I find previous year CAT questions related to generic puzzles? |  |