CAT Previous Year Questions: Routes & Network | Logical Reasoning (LR) and Data Interpretation (DI) PDF Download
From 2021 to 2024, the CAT exam has included questions on routes and networks, focusing on optimising travel paths, managing network constraints, and analysing relationships within structured systems. These questions test logical reasoning, distance calculations, and probabilistic outcomes, with scenarios involving walkways, metro systems, supply routes, and social networks.

2024
Passage - 1
Answer the following questions based on the information given below.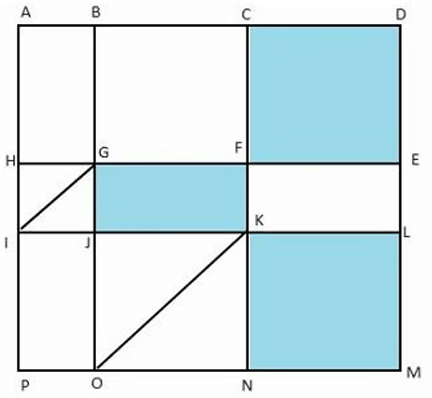
The above is a schematic diagram of walkways (indicated by all the straight-lines) and lakes (3 of them, each in the shape of rectangles – shaded in the diagram) of a gated area. Different points on the walkway are indicated by letters (A through P) with distances being OP = 150 m, ON = MN = 300 m, ML = 400 m, EL = 200 m, DE = 400 m.The following additional information about the facilities in the area is known.
1. The only entry/exit point is at C.
2. There are many residences within the gated area; all of them are located on the path AH and ML with four of them being at A, H, M, and L.
3. The post office is located at P and the bank is located at B.
Q1: One resident whose house is located at L, needs to visit the post office as well as the bank. What is the minimum distance (in m) he has to walk starting from his residence and returning to his residence after visiting both the post office and the bank?
(a) 3000
(b) 2700
(c) 3100
(d) 3200
Ans: (a)
Sol: The path that the resident can take to minimize the distance is L-E-D-C-B-G-I-P-O-K-L, So the total distance = 200+ 400+ 300+ 300+400+250+400+150+500+300 = 3200 meters
Q2: One person enters the gated area and decides to walk as much as possible before leaving the area without walking along any path more than once and always walking next to one of the lakes. Note that he may cross a point multiple times. How much distance (in m) will he walk within the gated area?
(a) 3200
(b) 3800
(c) 2800
(d) 3000
Ans: (b)
Sol: The maximum distance, in this case, is nothing but the sum of the perimeters of all the lakes i.e. 1000+ 1400+ 1400 = 3800
Q3: One resident takes a walk within the gated area starting from A and returning to A without going through any point (other than A) more than once. What is the maximum distance (in m) she can walk in this way?
Ans: 5100
Sol: The maximum distance, in this case is 5100 meters.
Q4: Visitors coming for morning walks are allowed to enter as long as they do not pass by any of the residences and do not cross any point (except C) more than once. What is the maximum distance (in m) that such a visitor can walk within the gated area?
Ans: 3500
Sol: The maximum distance can be covered by using the path C-B-G-J-I-P-O-N-K-F-E-D-C. So the total distance = 300+ 400+ 200+ 150+ 400+ 150+ 300+ 400+ 200+ 300+ 400+ 300 = 3500 meters.
Passage - 2
Answer the following questions based on the information given below.
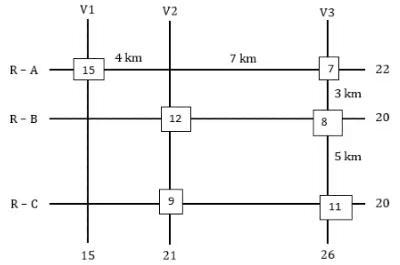
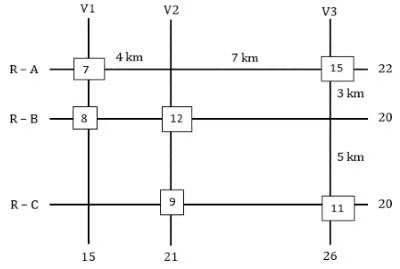
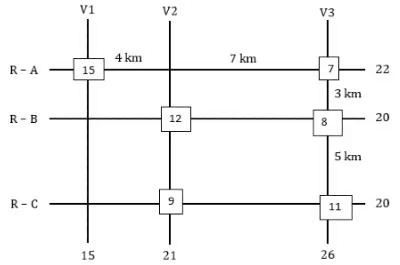
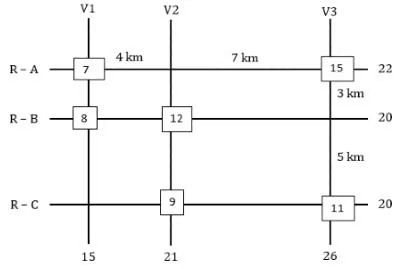
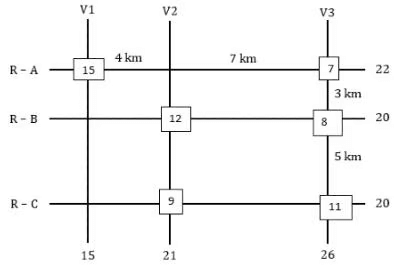
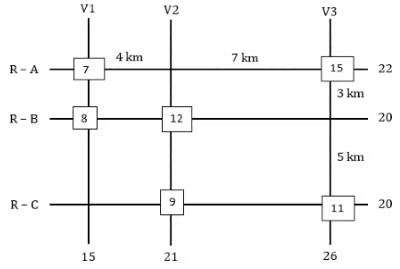
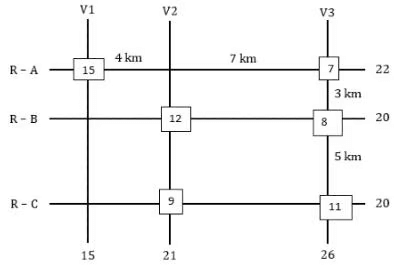
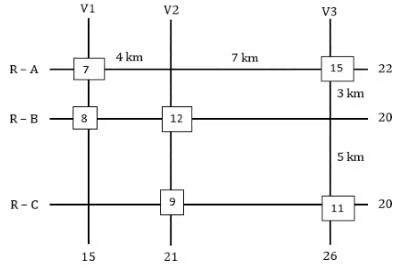
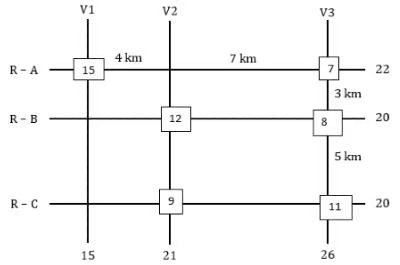
The figure below shows a network with three parallel roads represented by horizontal lines R-A, R-B, and R-C and another three parallel roads represented by vertical lines V1, V2, and V3. The figure also shows the distance (in km) between two adjacent intersections. Six ATMs are placed at six of the nine road intersections. Each ATM has a distinct integer cash requirement (in Rs. Lakhs), and the numbers at the end of each line in the figure indicate the total cash requirements of all ATMs placed on the corresponding road. For example, the total cash requirement of the ATM(s) placed on road R-A is Rs. 22 Lakhs.
The following additional information is known.
1. The ATMs with the minimum and maximum cash requirements of Rs. 7 Lakhs and Rs. 15 Lakhs are placed on the same road.
2. The road distance between the ATM with the second highest cash requirement and the ATM located at the intersection of R-C and V3 is 12 km.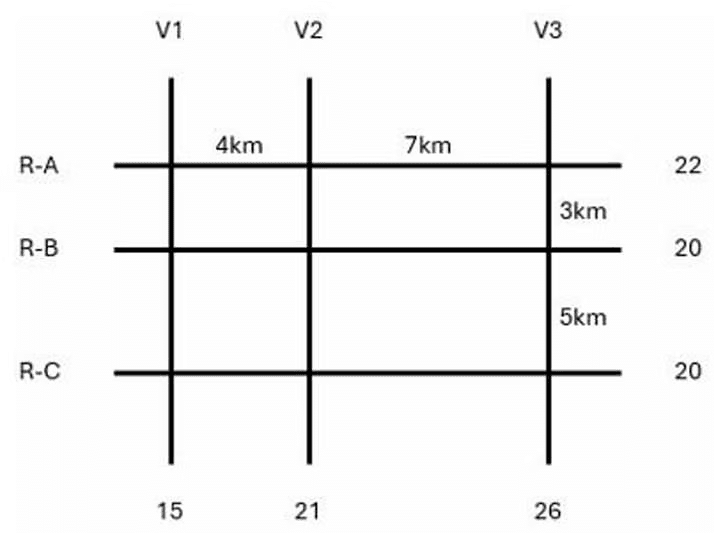
Q1: Which of the following statements is correct?
(a) The cash requirement of the ATM placed at the (R-C, V2) intersection cannot be uniquely determined.
(b) The ATM placed at the (R-C, V2) intersection has a cash requirement of Rs. 8 Lakhs.
(c) The ATM placed at the (R-C, V2) intersection has a cash requirement of Rs. 9 Lakhs.
(d) There is no ATM placed at the (R-C, V2) intersection.
Ans: c
Sol: It is given that all the amounts required are in lakhs and are unique between 7 and 15 both inclusive. So, the six amounts should be among 7, 8, 9, 10, 11, 12, 13, 14, and 15. The ATMs requiring amounts 7 and 15 lakhs are on the same road so the only possible road is R-A which has a total of 22 lakhs.
From statement 2 we can say that there is an ATM at R-B: V2 which is of the second highest amount and one is at R-C: V3. Now we know that the ATM at R-B: V2 needs to be of second highest and it must also satisfy the road sum of 20 lakhs. The possible combinations are 12+8 or 11+9, as we can see the road sum of R-C is also 20 and it can only have two possible combinations 12+8 or 11+9, since the ATM at R-B: V2 needs to be of second highest we take the ATMs along the road R-B as (12+8) and the ATM’s along the road R-C as (11+9). The sum along the road V1 is 15 so we can say that neither 9 nor 11 is at the intersection R-C: V1. The sum along road V2 must be 21, we already have 12, so we need another 9, so there will be an ATM at the intersection of R-C: V2 which needs 9 lakhs, and the ATM at R-C: V3 which requires 11 lakhs. With this information, we get two cases.Case-1:
Case-2:
Q2: How many ATMs have cash requirements of Rs. 10 Lakhs or more?
Ans: 3
Sol: It is given that all the amounts required are in lakhs and are unique between 7 and 15 both inclusive. So, the six amounts should be among 7, 8, 9, 10, 11, 12, 13, 14, and 15. The ATMs requiring amounts 7 and 15 lakhs are on the same road so the only possible road is R-A which has a total of 22 lakhs.
From statement 2 we can say that there is an ATM at R-B: V2 which is of the second highest amount and one is at R-C: V3. Now we know that the ATM at R-B: V2 needs to be of second highest and it must also satisfy the road sum of 20 lakhs. The possible combinations are 12+8 or 11+9, as we can see the road sum of R-C is also 20 and it can only have two possible combinations 12+8 or 11+9, since the ATM at R-B: V2 needs to be of second highest we take the ATMs along the road R-B as (12+8) and the ATM’s along the road R-C as (11+9). The sum along the road V1 is 15 so we can say that neither 9 nor 11 is at the intersection R-C: V1. The sum along road V2 must be 21, we already have 12, so we need another 9, so there will be an ATM at the intersection of R-C: V2 which needs 9 lakhs, and the ATM at R-C: V3 which requires 11 lakhs. With this information, we get two cases.Case-1:
Case-2:
Q3: Which of the following two statements is/are DEFINITELY true?
Statement A: Each of R-A, R-B, and R-C has two ATMs.
Statement B: Each of V1, V2, and V3 has two ATMs.
(a) Only Statement A
(b) Both Statement A and Statement B
(c) Neither Statement A nor Statement B
(d) Only Statement B
Ans: a
Sol: It is given that all the amounts required are in lakhs and are unique between 7 and 15 both inclusive. So, the six amounts should be among 7, 8, 9, 10, 11, 12, 13, 14, and 15. The ATMs requiring amounts 7 and 15 lakhs are on the same road so the only possible road is R-A which has a total of 22 lakhs.
From statement 2 we can say that there is an ATM at R-B: V2 which is of the second highest amount and one is at R-C: V3. Now we know that the ATM at R-B: V2 needs to be of second highest and it must also satisfy the road sum of 20 lakhs. The possible combinations are 12+8 or 11+9, as we can see the road sum of R-C is also 20 and it can only have two possible combinations 12+8 or 11+9, since the ATM at R-B: V2 needs to be of second highest we take the ATMs along the road R-B as (12+8) and the ATM’s along the road R-C as (11+9). The sum along the road V1 is 15 so we can say that neither 9 nor 11 is at the intersection R-C: V1. The sum along road V2 must be 21, we already have 12, so we need another 9, so there will be an ATM at the intersection of R-C: V2 which needs 9 lakhs, and the ATM at R-C: V3 which requires 11 lakhs. With this information, we get two cases.Case-1:
Case-2:
Q4: What best can be said about the road distance (in km) between the ATMs having the second highest and the second lowest cash requirements?
(a) Either 4 km or 7 km
(b) 5 km
(c) 7 km
(d) 4 km
Ans: a
Sol: It is given that all the amounts required are in lakhs and are unique between 7 and 15 both inclusive. So, the six amounts should be among 7, 8, 9, 10, 11, 12, 13, 14, and 15. The ATMs requiring amounts 7 and 15 lakhs are on the same road so the only possible road is R-A which has a total of 22 lakhs.
From statement 2 we can say that there is an ATM at R-B: V2 which is of the second highest amount and one is at R-C: V3. Now we know that the ATM at R-B: V2 needs to be of second highest and it must also satisfy the road sum of 20 lakhs. The possible combinations are 12+8 or 11+9, as we can see the road sum of R-C is also 20 and it can only have two possible combinations 12+8 or 11+9, since the ATM at R-B: V2 needs to be of second highest we take the ATMs along the road R-B as (12+8) and the ATM’s along the road R-C as (11+9). The sum along the road V1 is 15 so we can say that neither 9 nor 11 is at the intersection R-C: V1. The sum along road V2 must be 21, we already have 12, so we need another 9, so there will be an ATM at the intersection of R-C: V2 which needs 9 lakhs, and the ATM at R-C: V3 which requires 11 lakhs. With this information, we get two cases.Case-1:
Case-2:
Q5: What is the number of ATMs whose locations and cash requirements can both be uniquely determined?
Ans: 3
Sol: It is given that all the amounts required are in lakhs and are unique between 7 and 15 both inclusive. So, the six amounts should be among 7, 8, 9, 10, 11, 12, 13, 14, and 15. The ATMs requiring amounts 7 and 15 lakhs are on the same road so the only possible road is R-A which has a total of 22 lakhs.
From statement 2 we can say that there is an ATM at R-B: V2 which is of the second highest amount and one is at R-C: V3. Now we know that the ATM at R-B: V2 needs to be of second highest and it must also satisfy the road sum of 20 lakhs. The possible combinations are 12+8 or 11+9, as we can see the road sum of R-C is also 20 and it can only have two possible combinations 12+8 or 11+9, since the ATM at R-B: V2 needs to be of second highest we take the ATMs along the road R-B as (12+8) and the ATM’s along the road R-C as (11+9). The sum along the road V1 is 15 so we can say that neither 9 nor 11 is at the intersection R-C: V1. The sum along road V2 must be 21, we already have 12, so we need another 9, so there will be an ATM at the intersection of R-C: V2 which needs 9 lakhs, and the ATM at R-C: V3 which requires 11 lakhs. With this information, we get two cases.Case-1:
Case-2:
2022
Passage - 1
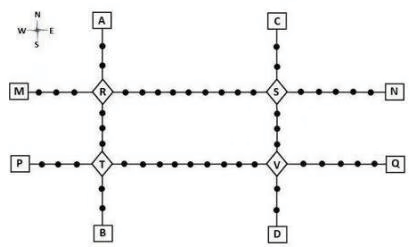 Given above is the schematic map of the metro lines in a city with rectangles denoting terminal stations (e.g. A), diamonds denoting junction stations (e.g. R) and small filled-up circles denoting other stations. Each train runs either in east-west or north-south direction, but not both. All trains stop for 2 minutes at each of the junction stations on the way and for 1 minute at each of the other stations. It takes 2 minutes to reach the next station for trains going in east-west direction and 3 minutes to reach the next station for trains going in north-south direction. From each terminal station, the first train starts at 6 am; the last trains leave the terminal stations at midnight. Otherwise, during the service hours, there are metro service every 15 minutes in the north-south lines and every 10 minutes in the east-west lines. A train must rest for at least 15 minutes after completing a trip at the terminal station, before it can undertake the next trip in the reverse direction. (All questions are related to this metro service only. Assume that if someone reaches a station exactly at the time a train is supposed to leave, (s)he can catch that train.)
Given above is the schematic map of the metro lines in a city with rectangles denoting terminal stations (e.g. A), diamonds denoting junction stations (e.g. R) and small filled-up circles denoting other stations. Each train runs either in east-west or north-south direction, but not both. All trains stop for 2 minutes at each of the junction stations on the way and for 1 minute at each of the other stations. It takes 2 minutes to reach the next station for trains going in east-west direction and 3 minutes to reach the next station for trains going in north-south direction. From each terminal station, the first train starts at 6 am; the last trains leave the terminal stations at midnight. Otherwise, during the service hours, there are metro service every 15 minutes in the north-south lines and every 10 minutes in the east-west lines. A train must rest for at least 15 minutes after completing a trip at the terminal station, before it can undertake the next trip in the reverse direction. (All questions are related to this metro service only. Assume that if someone reaches a station exactly at the time a train is supposed to leave, (s)he can catch that train.)
Q1: If Hari is ready to board a train at 8:05 am from station M, then when is the earliest that he can reach station N?
(a) 9:01 am
(b) 9:11 am
(c) 9:13 am
(d) 9:06 am
Ans: b
Sol: In the east-west direction, a train starts from station M every 10 minutes.
Now the first train leaving station M is at 6:00 am.
Since every 10 minutes trains are available in east-west direction, the train timings leaving from M will be like 6:10 am, 6:20 am, 6:30 am and so on.
Given, Hari has reached station M by 8:05 am.
So the earliest by which Hari can catch a train from station M is 8:10 am.
Now there are 19 stations between M and n, out of which two stations are junctions.
Time taken to travel between two stations in the east-west direction is 2 minutes.
Therefore, the time for which the train was running between M and N (excluding the stoppage time) = 20 × 2 = 40 minutes
Stoppage time at a junction is 2 minutes, while at the rest of the stations, it is 1 minute each.
Stoppage time for the train running between M and N = (17 × 1) + (2 × 2) = 21 minutes
Therefore, total travel time = 40+21 = 61 minutes.
So the time by which Hari reaches N is 8:10 am + 61 minutes = 9:11 am
Q2: If Priya is ready to board a train at 10:25 am from station T, then when is the earliest that she can reach station S?
(a) 11:12 am
(b) 11:07 am
(c) 11:22 am
(d) 11:28 am
Ans: a
Sol: Priya can reach S from T via R or V.
Case 1 :- T-V-S
In the east-west direction, the first train from P arrives at T at time = 6 am + (4 x 2) + (3 x 1) = 11 minutes = 6:11 am
Since T is a junction so this train will halt for 2 minutes at T and leave at 6:13.
Priya boards a east-west train then Priya will board a train for V from T at 10:33 am.
There are 9 stations between T and V
Travelling time between T and V = (10 x 2) + (9 x 1) = 29 minutes
Therefore, Priya will reach V latest by 10:33 am + 29 minutes = 11:02 am
In the north-south direction, the first train from D arrives at V at time = 6 am + (3 x 3) + (2 x 1) = 11 minutes = 6:11 am
Since V is a junction so this train will halt for 2 minutes at V and leave at 6:13.
Since every 15 minutes, a train starts from D in the north-south direction, so the latest by which Priya will be able to board such a train from V is at 11:13 am.
There are 3 stations between V and S
Travelling time between R and S =(4 x 3) + (3 × 1) = 15 minutes
Time by which she reaches S = 11:13 +15 minutes = 11:28 am
Case 2 :- T-R-S
In the north-south direction, the first train from B arrives at T at time = 6 am + (3 x 3) + (2×1) = 11 minutes = 6:11 am
Since T is a junction so this train will halt for 2 minutes at T and leave at 6:13.
Since every 15 minutes a train starts from P in the east-west direction so the latest by which Priya will be able to board such a train is at 10:28 am.
Now since she will be able to board a north-south train earlier than the east-west train so Priya will board a train for R from T at 10:28 am.
There are 3 stations between T and R
Travelling time between T and R = (4 x 3) + (3 × 1) = 15 minutes
Therefore, Priya will reach R latest by 10:43 am
In the east-west direction, the first train from M arrives at R at time = 6 am + (4× 2) + (3×1) = 11 minutes= 6:11 am
Since R is a junction so this train will halt for 2 minutes at R and leave at 6:13.
Since every 10 minutes, a train starts from M in the east-west direction, so the latest by which Priya will be able to board such a train is at 10:43 am.
There are 9 stations between R and S
Travelling time between R and S = (10 x 2) + (9 x 1) = 29 minutes
Time by which she reaches S = 10:43 +29 minutes = 11:12 am
We are getting shorter time in case 2. So 11:12 am is the answer
Q3: Haripriya is expected to reach station S late. What is the latest time by which she must be ready to board at station S if she must reach station B before 1 am via station R?
(a) 11:35 pm
(b) 11:43 pm
(c) 11:49 am
(d) 11:39 pm
Ans: d
Sol: Travelling time between S and R = (10 x 2) + (9 x 1) = 29 minutes
There is a stoppage of 2 minutes at R
Travelling time between R and B = (7 x 3) + (1 × 2) + (5 × 1) = 28 minutes
In the north-south direction, the first train from A arrives at R at time = 6 am +(3 x 3) + (2x1) =6:11 am.
Since R is a junction so this train will halt for 2 minutes at R and leave at 6:13.
Every 15 minutes, a train starts from A in the north-south direction.
The last train that leaves A will be at 12:00 am and it will leave R at 12:13 am, so Haripriya must reach R till 12:13 am.
Travelling time between S and R = (10 x 2) + (9 x 1) = 29 minutes
So Haripriya must board the train at S by 11:44 pm
In the east-west direction, the first train from N arrives at S at time = 6 am +(6 x 2) + (5×1) =6:17 am.
Since S is a junction so this train will halt for 2 minutes at S and leave at 6:19.
Every 10 minutes, a train starts from N in the east-west direction.
Therefore, Haripriya should board the train which leaves S at 11:39.
Q4: What is the minimum number of trains that are required to provide the service on the AB line (considering both north and south directions)?
Ans: 8
Sol: Travel time between A and B = (10 x 3) + (7 x 1) + (2 × 2) = 41 minutes
After completing a journey, a train must rest for 15 minutes at least before starting again.
So if a train starts from 6 am from A to B, then the latest by which that train will start from B to A will be at 7 am, as in the north-south direction, a train starts from A and B every 15 minutes.
So the total no. of trains required = (60/15) x 2 = 8
Q5: What is the minimum number of trains that are required to provide the service in this city?
Ans: 48
Sol: Travel time between A and B = (10 x 3) + (7 x 1) + (2 x 2) = 41 minutes
After completing a journey, a train must rest for 15 minutes at least before starting again.
So if a train starts from 6 am from A to B, then the latest by which that train will start from B to A will be at 7 am, as in the north-south direction, a train starts from A and B every 15 minutes.
So the total no. of trains required for the north-south lines = (60/15) x 2 x 2 = 16
Travel time between M and N = (20 x 2) + (17 x 1) + (2 x 2) = 61 minutes
After completing a journey, a train must rest for 15 minutes at least before starting again.
So if a train starts from 6 am from M to N, then the latest by which that train will start from N to M will be at 7:20 am, as in the east-west direction, a train starts from M and N every 15 minutes.
So the total no. of trains required for the east-west lines= (80/10) x 2 x 2 = 32
Total no. of trains required to service the city = 16+32 = 48
Passage - 2
Every day a widget supplier supplies widgets from the warehouse (W) to four locations – Ahmednagar (A), Bikrampore (B), Chitrachak (C), and Deccan Park (D). The daily demand for widgets in each location is uncertain and independent of each other. Demands and corresponding probability values (in parenthesis) are given against each location (A, B, C, and D) in the figure below. For example, there is a 40% chance that the demand in Ahmednagar will be 50 units and a 60% chance that the demand will be 70 units. The lines in the figure connecting the locations and warehouse represent two-way roads connecting those places with the distances (in km) shown beside the line. The distances in both the directions along a road are equal. For example, the road from Ahmednagar to Bikrampore and the road from Bikrampore to Ahmednagar are both 6 km long.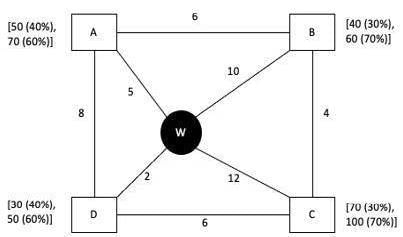
Every day the supplier gets the information about the demand values of the four locations and creates the travel route that starts from the warehouse and ends at a location after visiting all the locations exactly once. While making the route plan, the supplier goes to the locations in decreasing order of demand. If there is a tie for the choice of the next location, the supplier will go to the location closest to the current location. Also, while creating the route, the supplier can either follow the direct path (if available) from one location to another or can take the path via the warehouse. If both paths are available (direct and via warehouse), the supplier will choose the path with minimum distance.
Q1: If the last location visited is Ahmednagar, then what is the total distance covered in the route (in km)?
Ans: 35
Sol:
The last location visited is A
=> Demand at A must be 50. It can’t be 70 as then 2 locations (B and C) will definitely have a demand less than 70 and in that case, A won’t be the last location to visit as visits happen in the decreasing order of demands.
Also, demand at all other locations must be greater than or equal to 50.
So, B = 60, D = 50 and C can be either 70 or 100 which wouldn’t matter as in any case it will be the highest, and the first to be visited.
Hence, the path that will be followed is CBDA.
Distance covered = WC + CB + BWD + DWA (DWA < DA) = 12 + 4 + 12 + 7 = 35 kms
Q2: If the total number of widgets delivered in a day is 250 units, then what is the total distance covered in the route (in km)?
Ans: 38
Sol:
250 is only possible for A = 70, B = 60, C = 70, D = 50
The path followed will be ACBD (since A is closer to W than C, we took AC instead of CA)
Distance covered = WA + AWC + CB + BWD = 5 + 17 + 4 + 12 = 38 kms
Q3: What is the chance that the total number of widgets delivered in a day is 260 units and the route ends at Bikrampore?
(a) 7.56%
(b) 17.64%
(c) 10.80%
(d) 33.33%
Ans: a
Sol: We can get 260 in the following 2 ways:
But the route ends at B only in the first way.
Hence, chance = 60% x 30% x 70% x 60% = 7.56%
Q4: If the first location visited from the warehouse is Ahmednagar, then what is the chance that the total distance covered in the route is 40 km?
(a) 18%
(b) 5.4%
(c) 30%
(d) 3.24%
Ans: a
Sol:
If first location is A, then chance that total distance covered is 40 km?
This is a question on Bayes’ Theorem.
A must be 70.
C will also be 70 as it can’t be 100.
So, ACBD (38 kms) or ACDB (5+17+6+12 = 40 kms)
i.e., D = 50, B = 40
Numerator = 60% x 30% x 60% x 30% = 324/104
In ACBD, BD can be (40,30), (60,50), (60,30)
i.e., in denominator we have 324/104 + 18/102 (12/102 + 42/102 + 28/102) = 1800/104
Required answer = 324/1800 = 18%
Q5: If Ahmednagar is not the first location to be visited in a route and the total route distance is 29 km, then which of the following is a possible number of widgets delivered on that day?
(a) 210
(b) 220
(c) 200
(d) 250
Ans: a
Sol:
A is not the first location to be visited. Total distance covered = 29 kms
CBAD is the only possibility.
Widgets delivered = 70+60+50+30 = 210 is a possibility.
2021
Passage
Amudha, Bharatan, Chandran, Dhinesh, Ezhil, Fani and Gowtham are seven people in a town. Any pair of them could either be strangers, acquaintances, or friends. All relationships are mutual. For example, if Amudha is a friend of Bharatan, then Bharatan is also a friend of Amudha. Similarly, if Amudha is a stranger to Bharatan, then Bharatan is also a stranger to Amudha.
Partial information about the number of friends, acquaintances, and strangers of each of these people among them is given in the table below.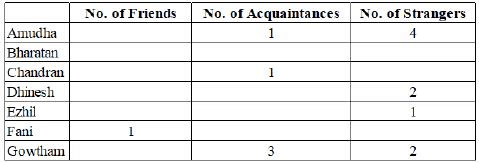
The following additional facts are also known.
Amudha, Dhinesh, and Fani are Ezil's friends.
- Chandran and Gowtham are friends.
- Every friend of Amudha is an acquaintance of Bharatan, and every acquaintance of Bharatan is a friend of Amudha.
- Every friend of Bharatan is an acquaintance of Amudha, and every acquaintance of Amudha is a friend of Bharatan.
- Amudha, Bharatan, and Chandran are mutual strangers.
Q1: Who are Gowtham’s acquaintances?
(a) Dhinesh, Ezhil and Fani
(b) Amudha, Dhinesh and Fani
(c) Bharatan, Dhinesh and Ezhil
(d) Amudha, Bharatan and Fani
Ans: a
Sol: Gowtham's Acquaintances are Ghinesh, Ezhil, Fani.
Q2: Which of these pairs share the same type of relationship?
(a) (Amudha, Gowtham) and (Ezhil, Fani)
(b) (Bharatan, Chandran) and (Dhinesh, Ezhil)
(c) (Chandran, Ezhil) and (Dhinesh, Gowtham)
(d) (Bharatan, Ezhil) and (Fani, Gowtham)
Ans: d
Sol: In the given options Bharatan and Ezhil are Acauaintances, Fani and Gowtham are acquaintances.
Q3: Who is an acquaintance of Amudha?
(a) Dhinesh
(b) Fani
(c) Gowtham
(d) Ezhil
Ans: a
Sol: Dhinesh is an acquaintance of Amudha
Q4: How many friends does Ezhil have?
Ans: 3
Sol: Ezhil has a total of 3 friends.
Q5: How many people are either a friend or a friend-of-a-friend of Ezhil?
Ans: 4
Sol: Ezhil has Amudha, Dhinesh, Fani as his friends. Dinesh has Bharatan as his friend. Hence a total of 4 (Amudha, Bharatan, Dhinesh, and Fani) are his friends or friend of a friend.
|
77 videos|180 docs|96 tests
|
FAQs on CAT Previous Year Questions: Routes & Network - Logical Reasoning (LR) and Data Interpretation (DI)
| 1. What are the key components of a transportation network? |  |
| 2. How do different modes of transport impact route planning? |  |
| 3. What role does technology play in modern transportation networks? |  |
| 4. What are the environmental impacts of transportation networks? |  |
| 5. How are transportation networks planned and managed? |  |