Q1: How many houses are vacant in Block XX?
Ans: 3
Sol:
It is given that some of the houses are occupied. The remaining ones are vacant and are the only ones available for sale.
The base price of a vacant house is Rs. 10 lakhs if the house does not have a parking space, and Rs. 12 lakhs if it does. The quoted price (in lakhs of Rs.) of a vacant house is calculated as (base price) + 5 × (road adjacency value) + 3 × (neighbor count).
It is also known that the maximum quoted price of a house in Block XX is Rs. 24 lakhs
Hence, there can be two cases for the maximum quoted price of a house in block XX.
Case 1: House with parking space:
=> 12+5a+3b = 24 => 5a+3b = 12 ( a = road adjacency value, b= neighbor count)
The only value for which the equation satisfies is (a = 0, and b=4). But the value of b can't be 4 because the maximum neighbor count can be at most 3.
Hence, case 1 is invalid.
Case 2: House without parking space:
=> 10+5a+3b = 24 => 5a+3b = 14
=> (a, b) = (1, 3)
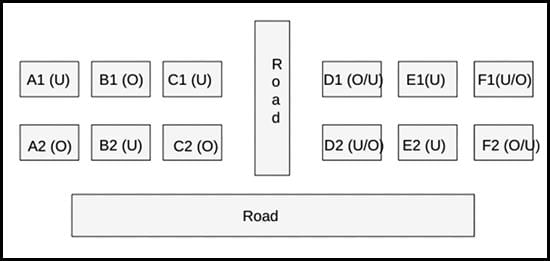
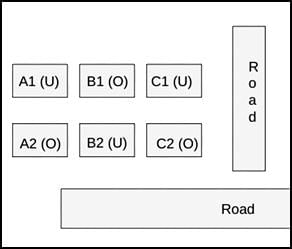
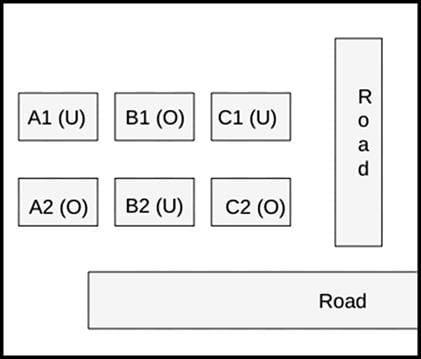
Hence, the house must have 3 neighbors and 1 road connected to it. Hence, the only possible case is B2. Therefore, the neighbor houses of B2, which are (B1, A2, and C2) are also occupied.
It is known that Row 1 has two occupied houses, one in each block. Since B1 is already occupied, it implies A1, and C1 are vacant.
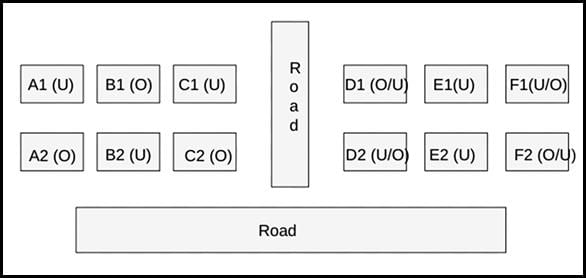
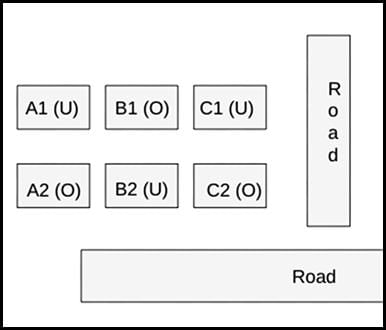
Hence, the configuration of block XX is given below: (Where U = Unoccupied/ Vacant, and U = Occupied)
Now for block YY, we know that both houses in Column E are vacant. Each of Column-D and Column-F has at least one occupied house. There is only one house with parking space in Block YY.
It is also known that the minimum quoted price of a house in block YY is Rs. 15 lakhs, and one such house is in Column E.
Case 1: The minimum quoted house is E2:
We know that the road adjacency of E2 is 1, hence we can calculate whether the house has parking space or not, and the neighbor count (b)
If the house has parking space, then: 12+5*1+3*b = 15 => 3b = -2 (which is not possible)
Hence, the house has no parking space => 10+5*1+3b = 15 => b = 0
b = 0 implies all the neighbor house of E2 is vacant, which are (E1, D2, and F2).
It is known that each of Column-D and Column-F has at least one occupied house, which implies D1, and F1 must be occupied.
But D1 and F1 can't be occupied together since the total number of occupied houses in Row 1 is 2 (one in each block).
Hence, This case is invalid.
Case 2: The minimum quoted house is E1:
We know that the road adjacency of E1 is 0, hence we can calculate whether the house has parking space or not, and the neighbor count (b).
i) If the house has no working space, then: 10+5*0+3b = 15 => b = 5/3 (this is not possible since b has to be an integer value)
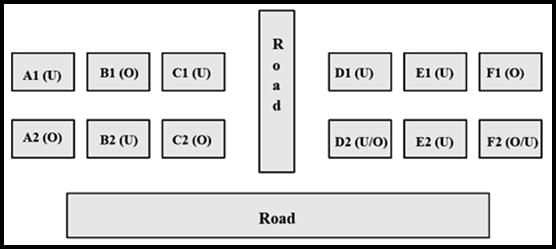
Hence, the house has parking space => 12+5*0+3b = 15 => b = 1 => One neighbor house is occupied among D1 and F1.
We already know that E2 is vacant. Among the houses D2, and F2, at least one must be occupied since each of Column-D and Column-F has at least one occupied house.
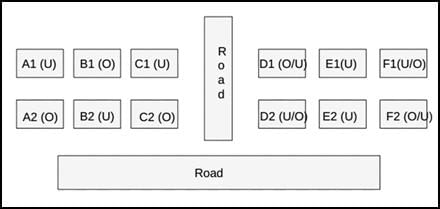
Therefore, the final diagram is given below:
From the diagram, we can see that 3 houses are vacant in block XX.
Q2: Which of the following houses is definitely occupied?
(a) A1
(b) D2
(c) B1
(d) F2
Ans: c
Sol:
It is given that some of the houses are occupied. The remaining ones are vacant and are the only ones available for sale.
The base price of a vacant house is Rs. 10 lakhs if the house does not have a parking space, and Rs. 12 lakhs if it does. The quoted price (in lakhs of Rs.) of a vacant house is calculated as (base price) + 5 × (road adjacency value) + 3 × (neighbor count).
It is also known that the maximum quoted price of a house in Block XX is Rs. 24 lakhs
Hence, there can be two cases for the maximum quoted price of a house in block XX.
Case 1: House with parking space:
=> 12+5a+3b = 24 => 5a+3b = 12 ( a = road adjacency value, b= neighbor count)
The only value for which the equation satisfies is (a = 0, and b=4). But the value of b can't be 4 because the maximum neighbor count can be at most 3.
Hence, case 1 is invalid.
Case 2: House without parking space:
=> 10+5a+3b = 24 => 5a+3b = 14
=> (a, b) = (1, 3)
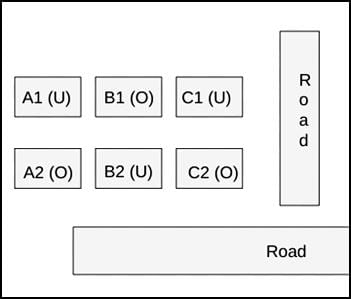
Hence, the house must have 3 neighbors and 1 road connected to it. Hence, the only possible case is B2. Therefore, the neighbor houses of B2, which are (B1, A2, and C2) are also occupied.
It is known that Row 1 has two occupied houses, one in each block. Since B1 is already occupied, it implies A1, and C1 are vacant.
Hence, the configuration of block XX is given below: (Where U = Unoccupied/ Vacant, and U = Occupied)
Now for block YY, we know that both houses in Column E are vacant. Each of Column-D and Column-F has at least one occupied house. There is only one house with parking space in Block YY.
It is also known that the minimum quoted price of a house in block YY is Rs. 15 lakhs, and one such house is in Column E.
Case 1: The minimum quoted house is E2:
We know that the road adjacency of E2 is 1, hence we can calculate whether the house has parking space or not, and the neighbor count (b)
If the house has parking space, then: 12+5*1+3*b = 15 => 3b = -2 (which is not possible)
Hence, the house has no parking space => 10+5*1+3b = 15 => b = 0
b = 0 implies all the neighbor house of E2 is vacant, which are (E1, D2, and F2).
It is known that each of Column-D and Column-F has at least one occupied house, which implies D1, and F1 must be occupied.
But D1 and F1 can't be occupied together since the total number of occupied houses in Row 1 is 2 (one in each block).
Hence, This case is invalid.
Case 2: The minimum quoted house is E1:
We know that the road adjacency of E1 is 0, hence we can calculate whether the house has parking space or not, and the neighbor count (b).
i) If the house has no working space, then: 10+5*0+3b = 15 => b = 5/3 (this is not possible since b has to be an integer value)
Hence, the house has parking space => 12+5*0+3b = 15 => b = 1 => One neighbor house is occupied among D1 and F1.
We already know that E2 is vacant. Among the houses D2, and F2, at least one must be occupied since each of Column-D and Column-F has at least one occupied house.
Therefore, the final diagram is given below:
From the diagram, we can see that B1 is definitely occupied. The rest opinions are not definitely correct.
The correct option is C
Q3: Which of the following options best describes the number of vacant houses in Row-2?
(a) Either 3 or 4
(b) Exactly 2
(c) Exactly 3
(d) Either 2 or 3
Ans: d
Sol:
It is given that some of the houses are occupied. The remaining ones are vacant and are the only ones available for sale.
The base price of a vacant house is Rs. 10 lakhs if the house does not have a parking space, and Rs. 12 lakhs if it does. The quoted price (in lakhs of Rs.) of a vacant house is calculated as (base price) + 5 × (road adjacency value) + 3 × (neighbor count).
It is also known that the maximum quoted price of a house in Block XX is Rs. 24 lakhs
Hence, there can be two cases for the maximum quoted price of a house in block XX.
Case 1: House with parking space:
=> 12+5a+3b = 24 => 5a+3b = 12 ( a = road adjacency value, b= neighbor count)
The only value for which the equation satisfies is (a = 0, and b=4). But the value of b can't be 4 because the maximum neighbor count can be at most 3.
Hence, case 1 is invalid.
Case 2: House without parking space:
=> 10+5a+3b = 24 => 5a+3b = 14
=> (a, b) = (1, 3)
Hence, the house must have 3 neighbors and 1 road connected to it. Hence, the only possible case is B2. Therefore, the neighbor houses of B2, which are (B1, A2, and C2) are occupied.
It is known that Row 1 has two occupied houses, one in each block. Since B1 is already occupied, it implies A1, and C1 are vacant.
Hence, the configuration of block XX is given below: (Where U = Unoccupied/ Vacant, and U = Occupied)
Now for block YY, we know that both houses in Column E are vacant. Each of Column-D and Column-F has at least one occupied house. There is only one house with parking space in Block YY.
It is also known that the minimum quoted price of a house in block YY is Rs. 15 lakhs, and one such house is in Column E.
Case 1: The minimum quoted house is E2:
We know that the road adjacency of E2 is 1, hence we can calculate whether the house has parking space or not, and the neighbor count (b)
If the house has parking space, then: 12+5*1+3*b = 15 => 3b = -2 (which is not possible)
Hence, the house has no parking space => 10+5*1+3b = 15 => b = 0
b = 0 implies all the neighbor house of E2 is vacant, which are (E1, D2, and F2).
It is known that each of Column-D and Column-F has at least one occupied house, which implies D1, and F1 must be occupied.
But D1 and F1 can't be occupied together since the total number of occupied houses in Row 1 is 2 (one in each block).
Hence, This case is invalid.
Case 2: The minimum quoted house is E1:
We know that the road adjacency of E1 is 0, hence we can calculate whether the house has parking space or not, and the neighbor count (b).
i) If the house has no working space, then: 10+5*0+3b = 15 => b = 5/3 (this is not possible since b has to be an integer value)
Hence, the house has parking space => 12+5*0+3b = 15 => b = 1 => One neighbor house is occupied among D1 and F1.
Let's take the case that house D1 is occupied and F1 is empty. In that case, the value of house F1 would be 10(there is no parking space)+ (5*0) + (3*the number of neighbours)
Here, even if we take the number of neighbours to be 1, which is maximum for F1 in this case, the value of F1 would be a maximum of 13. This is lower than the lowest value house in block YY. Therefore, F1 cannot be empty.
Let us see the other scenario of D1 being unoccupied.
Here, the value of D1 can be 15 or 18 depending on if D2 is unoccupied or occupied respectively.We do not know the status of houses D2 and F2.
Therefore, the final diagram is given below:
From the diagram, we can say that the number of vacant houses in Row 2 in Block XX is 1, and the number of vacant houses in Row 2 in Block YY is either 1 or 2.
Hence, the total number of vacant houses is either 2 or 3
The correct option is D
Q4: What is the maximum possible quoted price (in lakhs of Rs.) for a vacant house in Column-E?
Ans: 21
Sol:
It is given that some of the houses are occupied. The remaining ones are vacant and are the only ones available for sale.
The base price of a vacant house is Rs. 10 lakhs if the house does not have a parking space, and Rs. 12 lakhs if it does. The quoted price (in lakhs of Rs.) of a vacant house is calculated as (base price) + 5 × (road adjacency value) + 3 × (neighbor count).
It is also known that the maximum quoted price of a house in Block XX is Rs. 24 lakhs
Hence, there can be two cases for the maximum quoted price of a house in block XX.
Case 1: House with parking space:
=> 12+5a+3b = 24 => 5a+3b = 12 ( a = road adjacency value, b= neighbor count)
The only value for which the equation satisfies is (a = 0, and b=4). But the value of b can't be 4 because the maximum neighbor count can be at most 3.
Hence, case 1 is invalid.
Case 2: House without parking space:
=> 10+5a+3b = 24 => 5a+3b = 14
=> (a, b) = (1, 3)
Hence, the house must have 3 neighbors and 1 road connected to it. Hence, the only possible case is B2. Therefore, the neighbor houses of B2, which are (B1, A2, and C2) are also occupied.
It is known that Row 1 has two occupied houses, one in each block. Since B1 is already occupied, it implies A1, and C1 are vacant.
Hence, the configuration of block XX is given below: (Where U = Unoccupied/ Vacant, and U = Occupied)
Now for block YY, we know that both houses in Column E are vacant. Each of Column-D and Column-F has at least one occupied house. There is only one house with parking space in Block YY.
It is also known that the minimum quoted price of a house in block YY is Rs. 15 lakhs, and one such house is in Column E.
Case 1: The minimum quoted house is E2:
We know that the road adjacency of E2 is 1, hence we can calculate whether the house has parking space or not, and the neighbor count (b)
If the house has parking space, then: 12+5*1+3*b = 15 => 3b = -2 (which is not possible)
Hence, the house has no parking space => 10+5*1+3b = 15 => b = 0
b = 0 implies all the neighbor house of E2 is vacant, which are (E1, D2, and F2).
It is known that each of Column-D and Column-F has at least one occupied house, which implies D1, and F1 must be occupied.
But D1 and F1 can't be occupied together since the total number of occupied houses in Row 1 is 2 (one in each block).
Hence, This case is invalid.
Case 2: The minimum quoted house is E1:
We know that the road adjacency of E1 is 0, hence we can calculate whether the house has parking space or not, and the neighbor count (b).
i) If the house has no working space, then: 10+5*0+3b = 15 => b = 5/3 (this is not possible since b has to be an integer value)
Hence, the house has parking space => 12+5*0+3b = 15 => b = 1 => One neighbor house is occupied among D1 and F1.
We already know that E2 is vacant. Among the houses D2, and F2, at least one must be occupied since each of Column-D and Column-F has at least one occupied house.
Therefore, the final diagram is given below:
From the diagram, the vacant house with the maximum possible quoted price in column E is E2 when both D2 and F2 are occupied.
The maximum possible quoted price of E2 is 10+5*1+3*2 = 21 Lacs. ( E2 has no parking space because E1 has the parking space and it is given that there is only one house with parking space in Block YY.)
Q5: Which house in Block YY has parking space?
(a) E1
(b) F2
(c) E2
(d) F1
Ans: a
Sol:
It is given that some of the houses are occupied. The remaining ones are vacant and are the only ones available for sale.
The base price of a vacant house is Rs. 10 lakhs if the house does not have a parking space, and Rs. 12 lakhs if it does. The quoted price (in lakhs of Rs.) of a vacant house is calculated as (base price) + 5 × (road adjacency value) + 3 × (neighbor count).
It is also known that the maximum quoted price of a house in Block XX is Rs. 24 lakhs
Hence, there can be two cases for the maximum quoted price of a house in block XX.
Case 1: House with parking space:
=> 12+5a+3b = 24 => 5a+3b = 12 ( a = road adjacency value, b= neighbor count)
The only value for which the equation satisfies is (a = 0, and b=4). But the value of b can't be 4 because the maximum neighbor count can be at most 3.
Hence, case 1 is invalid.
Case 2: House without parking space:
=> 10+5a+3b = 24 => 5a+3b = 14
=> (a, b) = (1, 3)
Hence, the house must have 3 neighbors and 1 road connected to it. Hence, the only possible case is B2. Therefore, the neighbor houses of B2, which are (B1, A2, and C2) are also occupied.
It is known that Row 1 has two occupied houses, one in each block. Since B1 is already occupied, it implies A1, and C1 are vacant.
Hence, the configuration of block XX is given below: (Where U = Unoccupied/ Vacant, and U = Occupied)
Now for block YY, we know that both houses in Column E are vacant. Each of Column-D and Column-F has at least one occupied house. There is only one house with parking space in Block YY.
It is also known that the minimum quoted price of a house in block YY is Rs. 15 lakhs, and one such house is in Column E.
Case 1: The minimum quoted house is E2:
We know that the road adjacency of E2 is 1, hence we can calculate whether the house has parking space or not, and the neighbor count (b)
If the house has parking space, then: 12+5*1+3*b = 15 => 3b = -2 (which is not possible)
Hence, the house has no parking space => 10+5*1+3b = 15 => b = 0
b = 0 implies all the neighbor house of E2 is vacant, which are (E1, D2, and F2).
It is known that each of Column-D and Column-F has at least one occupied house, which implies D1, and F1 must be occupied.
But D1 and F1 can't be occupied together since the total number of occupied houses in Row 1 is 2 (one in each block).
Hence, This case is invalid.
Case 2: The minimum quoted house is E1:
We know that the road adjacency of E1 is 0, hence we can calculate whether the house has parking space or not, and the neighbor count (b).
i) If the house has no working space, then: 10+5*0+3b = 15 => b = 5/3 (this is not possible since b has to be an integer value)
Hence, the house has parking space => 12+5*0+3b = 15 => b = 1 => One neighbor house is occupied among D1 and F1.
We already know that E2 is vacant. Among the houses D2, and F2, at least one must be occupied since each of Column-D and Column-F has at least one occupied house.
Therefore, the final diagram is given below:
From the diagram, we can see that E1 has the parking space (case 2).
The correct option is A
Q6: Who among the following was DEFINITELY NOT ranked first in his/her group?
(a) Dipen
(b) Aruna
(c) Brij
(d) Chitra
Ans: a
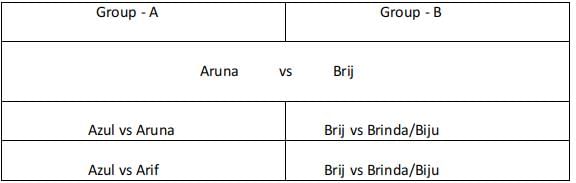
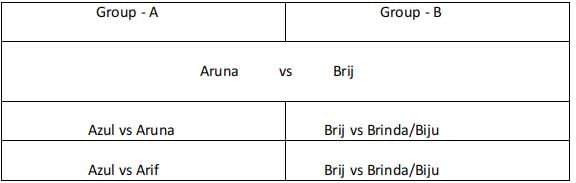
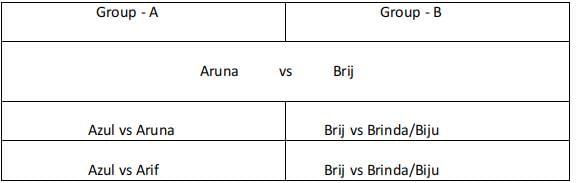
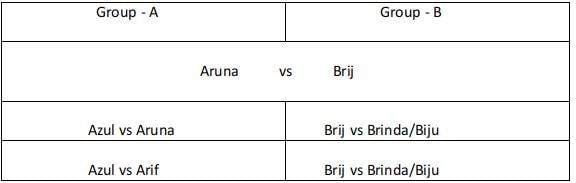
Sol: Group A :
Since Aruna played 3 games if she belongs to rank 2 or rank 3 in her group she must have reached the semifinals and lost in the semifinals. But for this case, she must play against rank 1 and rank 3 in her group. But she did not play against Arif from her group.
Hence Aruna was ranked 1 in her group, Among Azul and Arif one of them was ranked 2 and the other was ranked 3. Azul defeated Arif in the first round and in the second round lost to Aruna. Aruna played her first round with Azul and won the round and played against the winner from group B and defeated them and moved to the finals.
Group B :
Brij did not play against Brinda. Biju played three games, Brij and Brinda played one game each.
Since Brij and Brinda played only one game each one of them was ranked 1 and the other was ranked 2 and 3. Brij did not play against Brinda. We are aware that Aruna reached finals and hence the person from Group B did not reach the finals. Biju played three games and hence must have played with Brij/Brinda in the first round and won the round. Plays with Brij/ Brinda and wins the second round. Plays with Aruna and loses the third round.
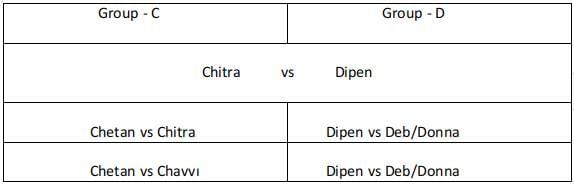
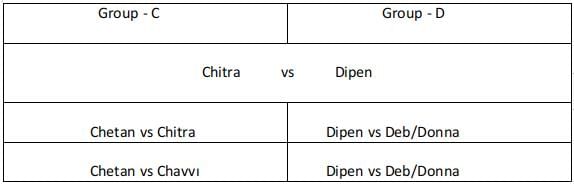
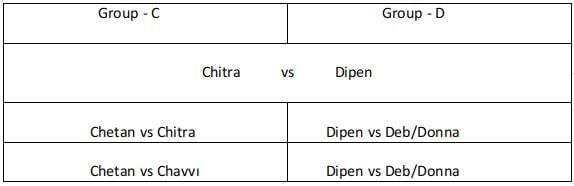
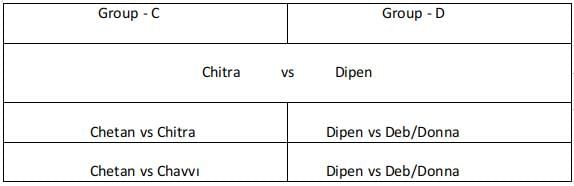
Group - C :
Chitra played 2 matches and Chetan played 2 matches. For Chitra to play 2 matches if she is rank 2 or rank 3 in her group. She must at least reach the semifinals. But in this case, Chetan will be defeated in his first round. So Chitra must be ranked 1 in her group and Chetan must be ranked 2 or rank 3 in his group. He defeats Chhavi in his first round and loses to Chitra in his second round. Chitra plays Chetan in her first round, wins over the winner of group D in her second round, and loses in the final against Aruna as per condition 1.
Group -D :
The person from Group D did not reach the finals because Chitra reached the finals. In order for Dipen to play 3 matches before his finals. Dipen must be ranked 2 or rank 3 in his group and plays Deb and Donna in the first two rounds in any order and wins over both of them. Dipen loses to Chitra in his third round.
Aruna plays Chitra in the finals and wins the final round.
Dipen was ranked 2 or 3 in his group
Q7: Who won the championship?
(a) Chitra
(b) Aruna
(c) Brij
(d) Cannot be determined
Ans: b
Sol: Group A :
Since Aruna played 3 games if she belongs to rank 2 or rank 3 in her group she must have reached the semifinals and lost in the semifinals. But for this case, she must play against rank 1 and rank 3 in her group. But she did not play against Arif from her group.
Hence Aruna was ranked 1 in her group, Among Azul and Arif one of them was ranked 2 and the other was ranked 3. Azul defeated Arif in the first round and in the second round lost to Aruna. Aruna played her first round with Azul and won the round and played against the winner from group B and defeated them and moved to the finals.
Group B :
Brij did not play against Brinda. Biju played three games, Brij and Brinda played one game each.
Since Brij and Brinda played only one game each one of them was ranked 1 and the other was ranked 2 and 3. Brij did not play against Brinda. We are aware that Aruna reached finals and hence the person from Group B did not reach the finals. Biju played three games and hence must have played with Brij/Brinda in the first round and won the round. Plays with Brij/ Brinda and wins the second round. Plays with Aruna and loses the third round.
Group - C :
Chitra played 2 matches and Chetan played 2 matches. For Chitra to play 2 matches if she is rank 2 or rank 3 in her group. She must at least reach the semifinals. But in this case, Chetan will be defeated in his first round. So Chitra must be ranked 1 in her group and Chetan must be ranked 2 or rank 3 in his group. He defeats Chhavi in his first round and loses to Chitra in his second round. Chitra plays Chetan in her first round, wins over the winner of group D in her second round, and loses in the final against Aruna as per condition 1.
Group -D :
The person from Group D did not reach the finals because Chitra reached the finals. In order for Dipen to play 3 matches before his finals. Dipen must be ranked 2 or rank 3 in his group and plays Deb and Donna in the first two rounds in any order and wins over both of them. Dipen loses to Chitra in his third round.
Aruna plays Chitra in the finals and wins the final round.
Aruna is the winner.
Q8: Which of the following pairs must have played against each other in the championship?
(a) Deb, Donna
(b) Azul, Biju
(c) Donna, Chetan
(d) Chitra, Dipen
Ans: d
Sol: Group A :
Since Aruna played 3 games if she belongs to rank 2 or rank 3 in her group she must have reached the semifinals and lost in the semifinals. But for this case, she must play against rank 1 and rank 3 in her group. But she did not play against Arif from her group.
Hence Aruna was ranked 1 in her group, Among Azul and Arif one of them was ranked 2 and the other was ranked 3. Azul defeated Arif in the first round and in the second round lost to Aruna. Aruna played her first round with Azul and won the round and played against the winner from group B and defeated them and moved to the finals.
Group B :
Brij did not play against Brinda. Biju played three games, Brij and Brinda played one game each.
Since Brij and Brinda played only one game each one of them was ranked 1 and the other was ranked 2 and 3. Brij did not play against Brinda. We are aware that Aruna reached finals and hence the person from Group B did not reach the finals. Biju played three games and hence must have played with Brij/Brinda in the first round and won the round. Plays with Brij/ Brinda and wins the second round. Plays with Aruna and loses the third round.
Group - C :
Chitra played 2 matches and Chetan played 2 matches. For Chitra to play 2 matches if she is rank 2 or rank 3 in her group. She must at least reach the semifinals. But in this case, Chetan will be defeated in his first round. So Chitra must be ranked 1 in her group and Chetan must be ranked 2 or rank 3 in his group. He defeats Chhavi in his first round and loses to Chitra in his second round. Chitra plays Chetan in her first round, wins over the winner of group D in her second round, and loses in the final against Aruna as per condition 1.
Group -D :
The person from Group D did not reach the finals because Chitra reached the finals. In order for Dipen to play 3 matches before his finals. Dipen must be ranked 2 or rank 3 in his group and plays Deb and Donna in the first two rounds in any order and wins over both of them. Dipen loses to Chitra in his third round.
Aruna plays Chitra in the finals and wins the final round.
Chitra and Dipen played in the semifinals
Q9: Who among the following did NOT play against Chitra in the championship?
(a) Aruna
(b) Chetan
(c) Dipen
(d) Biju
Ans: d
Sol: Group A :
Since Aruna played 3 games if she belongs to rank 2 or rank 3 in her group she must have reached the semifinals and lost in the semifinals. But for this case, she must play against rank 1 and rank 3 in her group. But she did not play against Arif from her group.
Hence Aruna was ranked 1 in her group, Among Azul and Arif one of them was ranked 2 and the other was ranked 3. Azul defeated Arif in the first round and in the second round lost to Aruna. Aruna played her first round with Azul and won the round and played against the winner from group B and defeated them and moved to the finals.
Group B :
Brij did not play against Brinda. Biju played three games, Brij and Brinda played one game each.
Since Brij and Brinda played only one game each one of them was ranked 1 and the other was ranked 2 and 3. Brij did not play against Brinda. We are aware that Aruna reached finals and hence the person from Group B did not reach the finals. Biju played three games and hence must have played with Brij/Brinda in the first round and won the round. Plays with Brij/ Brinda and wins the second round. Plays with Aruna and loses the third round.
Group - C :
Chitra played 2 matches and Chetan played 2 matches. For Chitra to play 2 matches if she is rank 2 or rank 3 in her group. She must at least reach the semifinals. But in this case, Chetan will be defeated in his first round. So Chitra must be ranked 1 in her group and Chetan must be ranked 2 or rank 3 in his group. He defeats Chhavi in his first round and loses to Chitra in his second round. Chitra plays Chetan in her first round, wins over the winner of group D in her second round, and loses in the final against Aruna as per condition 1.
Group -D :
The person from Group D did not reach the finals because Chitra reached the finals. In order for Dipen to play 3 matches before his finals. Dipen must be ranked 2 or rank 3 in his group and plays Deb and Donna in the first two rounds in any order and wins over both of them. Dipen loses to Chitra in his third round.
Aruna plays Chitra in the finals and wins the final round.
Brij was the player from group B who played Chitra. Aruna played in finals, Chetan in round 2, and Dipen in semi finals
FAQs on CAT Previous Year Questions: Arrangements
| 1. What are the common types of arrangement questions asked in the CAT exam? |  |
| 2. How can I effectively prepare for arrangement questions in the CAT? |  |
| 3. What strategies can be used to solve arrangement problems quickly? |  |
| 4. Are there any specific tips for handling circular arrangement questions? |  |
| 5. How important are arrangement questions in the overall CAT exam? |  |