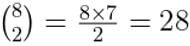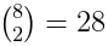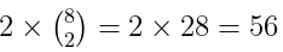Games & Tournaments | Logical Reasoning (LR) and Data Interpretation (DI) - CAT PDF Download
| Table of contents |

|
| Introduction |

|
| Round-Robin Tournaments |

|
| Knockout Tournaments |

|
| Hybrid Tournaments |

|
| Tips and Strategies |

|
Introduction
Games & Tournament problems often involve calculating matches, distributing points, and determining rankings across different formats. The three main types—Round-Robin, Knockout, and Hybrid require a clear understanding of rules, point systems, and progression stages. Mastering these concepts helps in solving questions quickly and accurately by applying the right formulas and logical steps.
Let us dive into the different types:
Round-Robin Tournaments
A round-robin tournament is a format where each participant plays every other participant exactly once (single round-robin) or twice (double round-robin).
1. Total Matches
For n teams:
- Single Round-Robin: Total matches are given by the combination formula:
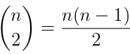 Example: For n = 8, total matches
Example: For n = 8, total matches 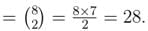
- Double Round-Robin: Each team plays every other team twice: n(n-1)
Example: For n = 8,
total matches = 8 x 7=56.
2. Points and Rankings
Points System: Typically, a win awards 2 points, a draw/tie awards 1 point, and a loss awards 0 points.
Total Points: Each match distributes exactly 2 points (either 2 to the winner or 1 to each team in a draw). Thus: Total Points = 2 x Total Matches
Wins, Losses, and Draws: Let:
- M: Total number of matches.
- W: Number of win-loss matches.
- D: Number of draw matches.
Then: M = W + D
Across all teams:
- Total wins (Wtotal) = W, as each win-loss match contributes one win.
- Total draws (Dtotal) = 2D, as each draw match contributes one draw to each of two teams.
- Total losses (Ltotal) = W, as each win-loss match contributes one loss.
The relationship is: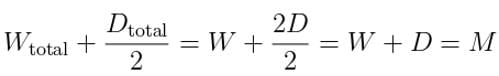
Solved Example
Consider a tournament with 16 teams divided into two groups of 8 each. Each group plays a single round-robin within itself. The top 4 teams from each group advance to Round 2, where each team from one group plays every team from the other group. After Round 2, the top 4 teams overall advance to the semi-finals, followed by the final. Points: Win = 2, Tie/Draw =1, Loss =0. Tie-breaker: Better run-rate.
Key Points:
- Total teams: 16
- Groups: A and B, each with 8 teams
- Points: Win = 2, Tie/Draw =1, Loss=0
- Advancement: Top 4 from each group to Round 2
- Round 2: Each team from Group A plays each team from Group B
- Final Stage: Top 4 overall to semi-finals, then final
- Tie-breaker: Run-rate
(i) Total number of matches played in the tournament?
Ans: 75
Group A Matches:
Group B Matches:
Round 2 Matches: Top 4 from A vs. Top 4 from B: 4 x 4 = 16
Semi-Finals: 2 matches
Final: 1 match
Total: 28 + 28 + 16 + 2 + 1 = 75
(ii) Least number of points to advance to Round 2?
Ans: To minimise points for a team to be in the top 4:
Maximise points for the top 3 teams:
- Team A (1st): Wins all 7 matches: 7 x 2 = 14 points
- Team B (2nd): Wins all except against A: 6 x 2 = 12 points
- Team C (3rd): Wins all except against A and B: 5 x 2 = 10 points
Total points in group:
Points used by top 3: 14 + 12 +10 = 36
Remaining points for bottom 5: 56- 36 = 20
Distribute among bottom 5:
- Bottom 5 play
= 10 mutual matches.
- If all are draws, each match gives 1 point to each team.
- Total points: 10x 2=20
- Each team plays 4 mutual matches, all draws: 4x 1 = 4 points
- Ranking: A: 14, B: 12, C: 10, D-H: 4 each
- A team with 4 points can be 4th with a better run-rate.
(iii) Maximum possible number of points for a team eliminated at the first round?
Ans: 10
To maximise points for the 5th-placed team:
Minimise points for the bottom 3 teams:
- They play
= 3 mutual matches.
- Each wins one match: Total points = 3 x 2 = 6
Remaining points for top 5: 56 - 6 = 50
Distribute equally: 50 ÷ 5 = 10 points each
The 5th team has 10 points but is eliminated due to run-rate.
(iv) Minimum number of matches won to reach the finals?
Ans:1
If all matches before the semi-finals are draws, a team advances via run-rate.
Winning only the semi-final (1 match) reaches the final.
(v) Maximum number of matches won to reach the finals?
Ans: 12
Win all group stage matches: 7
Win all Round 2 matches:
Win semi-final: 1
Total: 7+4+1=12
Knockout Tournaments
A knockout tournament eliminates one participant per match until a champion emerges.
Key properties:
- Total Matches: N - 1, where N is the number of participants.
- Rounds: If N = 2k, there are k rounds. Otherwise, byes are needed.
- Seeding: Higher seeds play lower seeds (e.g., #1 vs. #N).
- Upsets: Lower-seeded participant defeats a higher-seeded one.
Visual Representation of Knockout Tournament (8 Teams)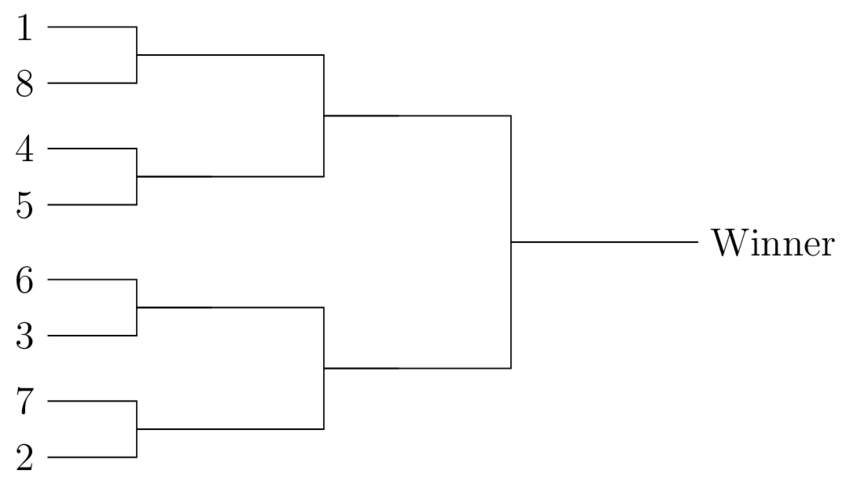
In this image,
The numbers 1 through 8 represent the seedings of the players or teams:
1 = Top seed (strongest competitor based on rankings/performance).
8 = Lowest seed (weakest competitor).
Seeds are arranged to avoid early clashes between top contenders (e.g., 1 and 2 can only meet in the final).
Bracket Logic
The bracket follows a mirrored pairing system to ensure fairness:
Top Half:
Match 1: 1 (1st seed) vs. 8 (8th seed)
Match 2: 4 (4th seed) vs. 5 (5th seed)
Bottom Half:
Match 3: 6 (6th seed) vs. 3 (3rd seed)
Match 4: 7 (7th seed) vs. 2 (2nd seed)
This ensures:
The highest seed (1) faces the lowest seed (8) in the first round.
The second-highest seed (2) faces the second-lowest seed (7).
Mid-tier seeds (3-6) face each other to balance competition.
Round 1 (Quarterfinals)
Four matches are played:
1 vs. 8 → Winner advances, loser eliminated.
4 vs. 5 → Typically the most balanced matchup.
6 vs. 3 → Potential for an upset (lower seed 6 could defeat higher seed 3).
7 vs. 2 → Higher seed (2) is favored, but upsets can happen.
Round 2 (Semifinals)
Winners from the top half (1/8 vs. 4/5) face each other.
Winners from the bottom half (6/3 vs. 7/2) face each other.
Final Round (Championship)
The last two remaining competitors play for the title of "Winner".
Solved Example
For a tournament with 75 players, each match is a knockout. If there are an odd number of players in any round, the top-seeded player gets a bye.
(i) If no byes from Round 2 onwards, how many matches in Round 1?
Ans: 11
Rounds: 26 < 75 < 27, so 7 rounds.
To have no byes from Round 2, Round 2 must have 2k players.
Closest 2k ≤ 75: 26 = 64.
Players eliminated in Round 1: 75 - 64 = 11.
Matches in Round 1: 11
(ii) If top-seeded players in quarterfinals and semi-finals are defeated, and one bye per round, what is the sum of ranks of finalists?
Ans: 6
Round 1: 75 players, 11 matches, 53 byes, 64 advance.
Assume top seed (#1) gets bye in rounds with odd players.
Quarterfinals (8 players): Top seed (#1) defeated.
Semi-finals: Next top seed (#2) defeated.
Finalists: #1 (via bye) and #5 (defeated #4 in semi-finals).
Sum of ranks: 1+5= 6.
Hybrid Tournaments
Hybrid tournaments combine round-robin and knockout formats:
- Group Stage: Round-robin within groups.
- Knockout Stage: Top teams advance to playoffs.
- Visual Representation of Hybrid Tournaments

In this image, there are following stages
Stage 1: Group Phase (Round-Robin)
Teams are split into two groups (e.g., Group 1: A, B, C, D; Group 2: E, F, G, H).
Each team plays every other team in their group.
The results (e.g., A1-B2, C1-D2) represent matches where:
The first letter (A, C, E, G) is the "home" or higher-seeded team.
The second letter (B, D, F, H) is the "away" or lower-seeded team.
The numbers (1, 2) likely indicate game scores or rankings (e.g., A1 = Team A’s first win, B2 = Team B’s second loss).
Stage 2: Crossover Knockout Matches
After the group stage, the top teams from each group face off in inter-group matches:
B1-A2 → 2nd-place from Group 1 vs. 1st-place from Group 2.
D1-C2 → 4th-place from Group 1 vs. 3rd-place from Group 2.
And so on.
This ensures:
Strong teams advance further.
Every match remains competitive (no dead rubbers).
Solved Example
Win-Loss Table For a 6-team round-robin tournament (15 matches):
- Points: Win = 2, Tie/Draw =1, Loss=0
Conditions:
- Two teams have the same points.
- Two pairs have the same number of wins.
- One pair has the same number of losses.
Solution:
Tips and Strategies
- Use diagrams for knockout tournaments to track opponents.
- Use tables for a round-robin to track points and wins.
- Memorise key formulas:
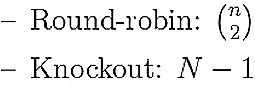
- For minimum points/wins, distribute from top to bottom.
- For maximum points/wins, distribute from bottom to top.
- Practice regularly to recognise patterns and solve efficiently.
|
77 videos|180 docs|96 tests
|
FAQs on Games & Tournaments - Logical Reasoning (LR) and Data Interpretation (DI) - CAT
| 1. What is a round-robin tournament and how does it work? |  |
| 2. How is a knockout tournament structured? |  |
| 3. What are the advantages of using a round-robin format over a knockout format? |  |
| 4. How are ties handled in round-robin tournaments? |  |
| 5. Can knockout tournaments include consolation rounds? |  |