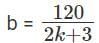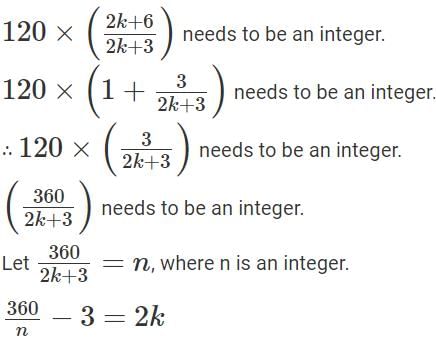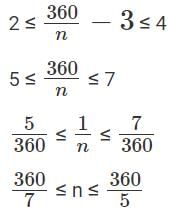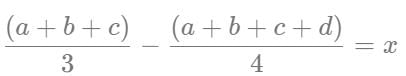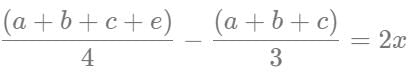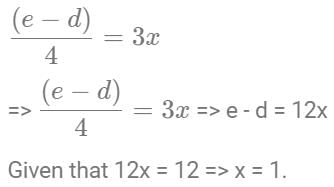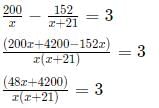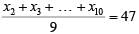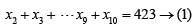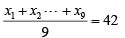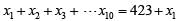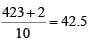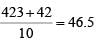2023
Q1: In an examination, the average marks of 4 girls and 6 boys is 24. Each of the girls has the same marks while each of the boys has the same marks. If the marks of any girl is at most double the marks of any boy, but not less than the marks of any boy, then the number of possible distinct integer values of the total marks of 2 girls and 6 boys is [2023]
(a) 19
(b) 21
(c) 20
(d) 22
Ans: b
Sol:
Let the marks of each girl in the class be g and the marks of each boy be b.
Since, the average marks of 4 girls and 6 boys is 24…
4g + 6b = 24 × 10 = 240
A girl scores more than or equal to the score of a boy but never more than double the score.
Therefore, g = kb, where 1 ≤ k ≤ 2
4(kb) + 6b = 240
b(4k + 6) = 240
b(2k + 3) = 120
Finally we need 2g + 6b = b(2k + 6) to be an integer.
Since, 1 ≤ k ≤ 2
2 ≤ 2k ≤ 4
51.42 ≤ n ≤ 72
52 ≤ n ≤ 72
Therefore, n can take 21 values, 52 to 72 both inclusive.
For all these values k takes a distinct value from 1 to 2 and 2g + 6b takes a distinct integral value.
Choice B is the correct answer.
Q2: There are three persons A, B and C in a room. If a person D joins the room, the average weight of the persons in the room reduces by x kg. Instead of D, if person E joins the room, the average weight of the persons in the room increases by 2x kg. If the weight of E is 12 kg more than that of D, then the value of x is [2023]
(a) 2
(b) 0.5
(c) 1
(d) 1.5
Ans: c
Sol:
Let us assume that A, B, C, D, and E weights are a, b, c, d, and e.
1st condition
2nd condition
Adding both the equations, we get:
2022
Q1: The average of a non-decreasing sequence of N numbers a1, a2,..., an is 300. If a1, is replaced by 6a1, the new average becomes 400. Then, the number of possible values of a1, is [2022]
Ans: 14
Sol:
a1 + a2 +.....+ aN = 300N
6a1 + a2 + .....+ aN = 400N
5a1 = 100N
a1 = 20N
As the given sequence of numbers is non-decreasing sequence, N can take values from 2 to 15.
N is not equal to 1, if N = 1, then average of N numbers is 300 wouldn't satisfy.
Therefore, N can take values from 2 to 15, i.e. 14 values.
Q2: Consider six distinct natural numbers such that the average of the two smallest numbers is 14, and the average of the two largest numbers is 28. Then, the maximum possible value of the average of these six numbers is [2022]
(a) 22.5
(b) 23.5
(c) 24
(d) 23
Ans: a
Sol:
We know the sum of the first pair of numbers is 14 * 2 = 28
Sum of the last pair of numbers is 28 * 2 = 56
To maximize the average of all the 6 numbers, we must try to maximize the two numbers in between. This is possible when the last pair of numbers are 27 and 29.
The maximum average case is
a, b, 25, 26, 27, 29
Where a + b = 28
The average of these 6 numbers is 22.5
2021
Q1: Suppose hospital A admitted 21 less Covid infected patients than hospital B, and all eventually recovered. The sum of recovery days for patients in hospitals A and B were 200 and 152, respectively. If the average recovery days for patients admitted in hospital A was 3 more than the average in hospital B then the number admitted in hospital A was [2021]
Ans: 35
Sol:
Let the number of Covid patients in Hospitals A and B be x and x+21 respectively. Then, it has been given that:
16x + 1400 = x(x + 21)
x2 + 5x − 1400 = 0
(x + 40)(x - 35) = 0
Hence, x = 35.
2020
Q1: In a group of 10 students, the mean of the lowest 9 scores is 42 while the mean of the highest 9 scores is 47. For the entire group of 10 students, the maximum possible mean exceeds the minimum possible mean by [2020]
(a) 4
(b) 3
(c) 5
(d) 6
Ans: aSol:
Let x1 be the least number
x10 be the largest number
Given
(1) - (2) = x10 - x1 = 45
Sum of 10 observations
Since the minimum value of x10 is 47, the minimum value of x1 is 2, minimum average
=
The maximum value of x1 is 42,
Maximum average =
Required difference = 4
2019
Q1: Ramesh and Gautam are among 22 students who write an examination. Ramesh scores 82.5. The average score of the 21 students other than Gautam is 62. The average score of all the 22 students is one more than the average score of the 21 students other than Ramesh. The score of Gautam is [2019]
(a) 51
(b) 53
(c) 49
(d) 48
Ans: a
Sol:
It is given that, a1, a2, a3,..... Ramesh, Gautham, ...., a22 writes an examination
Given that, Average score of the 21 students other than Gautham = 62
So, Total Score - Gautham's score = 62 x 21
Ramesh scored 82.5
It is given that, when Ramesh leaves, the average score drops down by 1 mark.
Which means that Ramesh scored more than the Overall class average.
Since his departure has resulted in the decrease of the overall class average by 1, his score is 21 more than the average.
Overall Class average = 82.5 - 21 = 61.5 marks
Total Score - Gautham's score = 62 x 21
Gautham's score = 61.5 x 22 - 62 x 21
Gautham's score = 1353 - 1302
Gautham's score = 51 marks
Q2: The average of 30 integers is 5. Among these 30 integers, there are exactly 20 which do not exceed 5. What is the highest possible value of the average of these 20 integers? [2019]
(a) 4
(b) 5
(c) 4.5
(d) 3.5
Ans: c
Sol:
We are told that exactly 20 of the 30 integers do not exceed 5.
That means exactly 10 of the 30 integers do exceed 5.
In order to keep the average of the 20 integers as high as possible, we need to keep the average of the 10 integers above 5 as low as possible.
Since we are dealing with integers, the least value that the 10 integers above 5 can take is 6.
So, the sum of the 10 integers = 10 * 6 = 60
So the sum of the remaining 20 integers = Total sum - 60 = 5 * 30 - 60 = 90
Hence the average of the remaining 20 is 90/20 = 4.5
Q3: In an apartment complex, the number of people aged 51 years and above is 30 and there are at most 39 people whose ages are below 51 years. The average age of all the people in the apartment complex is 38 years. What is the largest possible average age, in years, of the people whose ages are below 51 years? [2019]
(a) 25
(b) 26
(c) 27
(d) 28
Ans: d
Sol:
Let number of people aged below 51 years be n.Total number of people in a complex = 30 + n
Total age of people in a complex = (30 + n) × 38
Largest possible average age of people above 51 years is 51.
Total age of people above 51 years = 51 × 30
Total age of people below 51 years = (30 + n) × 38 - 51 × 30 = 38n - 390
Average age people below 51 years = (38n - 390)/n
Then,
For largest possible age, n = 39
∴ Required age = (38 - 390/39) = 28 years
2018
Q1: A CAT aspirant appears for a certain number of tests. His average score increases by 1 if the first 10 tests are not considered, and decreases by 1 if the last 10 tests are not considered. If his average scores for the first 10 and the last 10 tests are 20 and 30, respectively, then the total number of tests taken by him is [2018 TITA]
Ans: 60
Sol:
Let there be 'n' tests and the Overall Average score be k
Average (n) = k => Total marks = nk
So, when we ignore the first 10 questions,
Average (n-10) = k+1
Similarly, if we ignore the last 10 questions,
Average (first (n - 10)) = k - 1
It is given that when the first 10 tests are not considered, the overall average increases by 1 (Each question carries 20 marks)
Total marks – 20 × 10 = (k + 1) (n - 10)
kn – 200 = (k + 1) (n - 10) ---(1)
Similarly, If the last 10 tests are not considered, the overall average decreases by 1 (Each question carries 30 marks)
kn - 300 = (k - 1) (n - 10) ---(2)
Solving (1) and (2), we get
kn - 200 = (k + 1) (n - 10)
(-) kn - 300 = (k - 1) (n - 10)
-------------------------------------
100 = 2(n - 10)
50 = n - 10
n = 60 questions
2017
Q1: An elevator has a weight limit of 630 kg. It is carrying a group of people of whom the heaviest weighs 57 kg and the lightest weighs 53 kg. What is the maximum possible number of people in the group? [2017 TITA]
Ans: 11
Sol:
Given that an elevator has a weight limit of 630 kg.
It is carrying a group of people of whom the heaviest weighs 57 kg and the lightest weighs 53 kg.
We have to find the maximum possible number of people in the group.
We can take one person to be 57 kg and since they have asked for the maximum possible number of people it can accommodate in the lift we can take more no. of people with lightest weight.
So, at least one guy with 57 kg.
⟹ 630 – 57 = 573
⟹ 573 / 53 = 10.8 or at most there can 10 people.
Hence, 10 + 1 = 11 people
The maximum possible number of people in the group is 11.
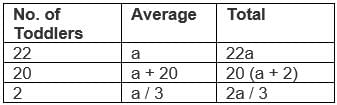
Q2: The average height of 22 toddlers increases by 2 inches when two of them leave this group. If the average height of these two toddlers is one-third the average height of the original 22, then the average height, in inches, of the remaining 20 toddlers is [2017]
(a) 30
(b) 28
(c) 32
(d) 26
Ans: c
Sol:
From the given data let us assume the average height of 22 toddlers to be a
If two of them leaves this group then average height of 20 toddlers increases by 2 so a + 2
If the average height of two toddlers who leaves the group is one third the average height of the original 22
No.of toddlers × average = Total
Hence we can write the equation in such a way that,
22a = 20(a + 2) + 2a / 3
2a – 2a / 3 = 40
⟹ 4a / 3 = 40
a = 30
We need to find the average of remaining 20 toddlers.
⟹ a + 2 = 30 + 2 = 32
FAQs on CAT Previous Year Questions: Averages
| 1. What are averages and how are they used in the CAT exam? |  |
| 2. How can I calculate the average of a set of numbers quickly? |  |
| 3. What types of questions related to averages can I expect in the CAT exam? |  |
| 4. Can you explain the concept of weighted average with an example? |  |
| 5. How can practice with previous year CAT questions on averages improve my score? |  |