TITA Based Questions: Games and Tournaments | Logical Reasoning (LR) and Data Interpretation (DI) - CAT PDF Download
As TITA (Type In The Answer) based questions are gaining prominence in the CAT exam, it’s important to build accuracy without relying on options. The following are carefully curated TITA-based questions on the topic Games and Tournaments to help you practice exact value-based problem solving.

Que 1: Instructions for Set 1 (2024)
The game of QUIET is played between two teams. Six teams, numbered 1, 2, 3, 4, 5, and 6, play in a QUIET tournament. These teams are divided equally into two groups. In the tournament, each team plays every other team in the same group only once, and each team in the other group exactly twice. The tournament has several rounds, each of which consists of a few games. Every team plays exactly one game in each round.
The following additional facts are known about the schedule of games in the tournament.
1. Each team played against a team from the other group in Round 8.
2. In Round 4 and Round 7, the match-ups, that is the pair of teams playing against each other, were identical. In Round 5 and Round 8, the match-ups were identical.
3. Team 4 played Team 6 in both Round 1 and Round 2.
4. Team 1 played Team 5 ONLY once and that was in Round 2.
5. Team 3 played Team 4 in Round 3. Team 1 played Team 6 in Round 6.
6. In Round 8, Team 3 played Team 6, while Team 2 played Team 5.
Q1: How many rounds were there in the tournament?
 View Answer
View Answer 
Ans: 8
We are told that there are six teams, that are divided into two groups.
Teams in the same group will play each other only once, and teams in different group will play each other twice.
Calculating the combinations, there is going to be 3C2 games among teams in the same group among them, and since there is two groups, total such games will be 6.
Now, teams in different group play each other twice. Calculating the combinations for this,
From the first group, a team can be chosen in three ways, and from the second group, a team can be chosen in three ways. Total ways two teams from different groups can play each other is 3 x 3 which is 9. And since they play each other twice, that is 9 + 9 games of this combination.
Total number of games is 18 + 6 = 24
It is given that each team plays one game in each round, that means there is going to be 3 matchups in each round. And given, there is 24 games to played in this format, the number of rounds will be 24/3 = 8
The tournament will have 8 rounds.
Now that we know there are going to be 8 rounds in the tournament, let us identify the teams in a particular group, that will help us build the matchups.
We are told that Round 8 teams from different groups play each other, and Teams 1 and 5 play only once. This means, 1 and 5 have to be on the same group. It is also told that 4 and 6 play each other twice, that means 4 and 6 have to be in different groups.
Looking at the matches from Round 8 that is given to us, 3 played 6 and 2 played 5. We already know 1 and 5 are in the same group, so 2 must be in the other group. Among 3 and 6, if we were to place 3 in the group with 1 and 5, 4 and 6 would have to be in the same group, which is not possible, hence 6 is with 1 and 5, giving us the final combination of groups.
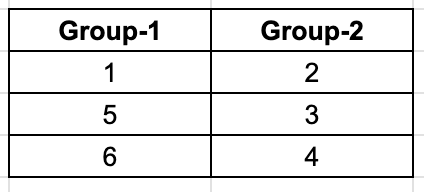 Now, using the given information to build the matchups for the 8 rounds.
Now, using the given information to build the matchups for the 8 rounds.
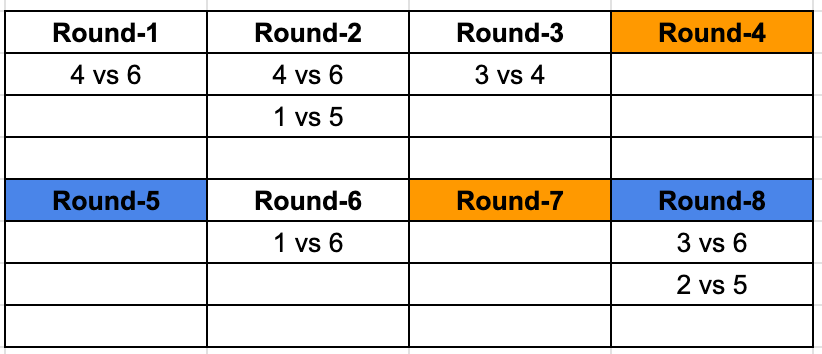
Rounds marked with the same colour represent the fact that the matchups are identical. Now we know that each team plays a game in each round, we know 2 out of the 3 matches for Round 2 and 8, and we can identify the third matchups as well. Giving us this resulting table.
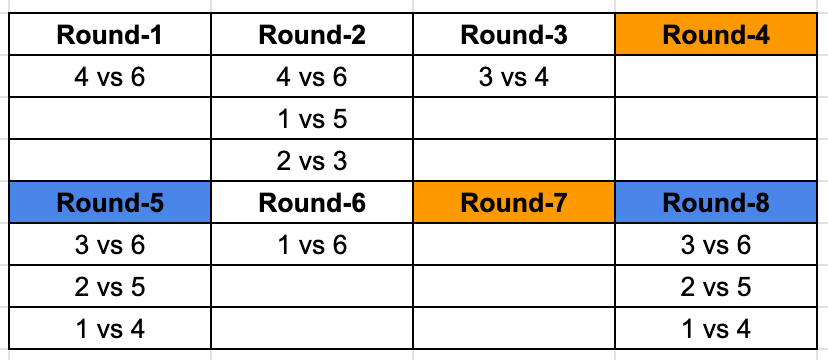 We are told that Round 4 and 7 are identical, that means they are the matchups between teams from two different groups,
We are told that Round 4 and 7 are identical, that means they are the matchups between teams from two different groups,
We look at the matchups that are remaining among the 6 teams where both the games are left to play.
Right away we identify that 6 is yet to play 2 twice and 5 once. We are looking for teams playing twice, so both Round 4 and 7 has a matchups between 2 and 6. This means 6 will play 5 in Round 3 and using that we can identify the third matchup in Round 3 as well.
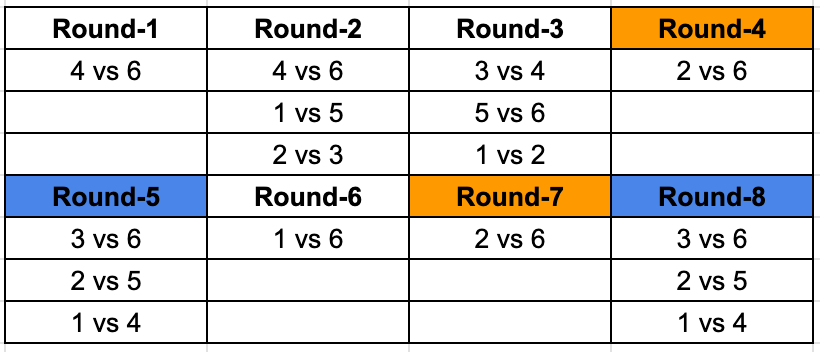
Now, we can identify that 1 is yet to play 3 both the times, 2 once. And we are looking for teams playing each other twice, so we can fill in the remaining values in the table as well.
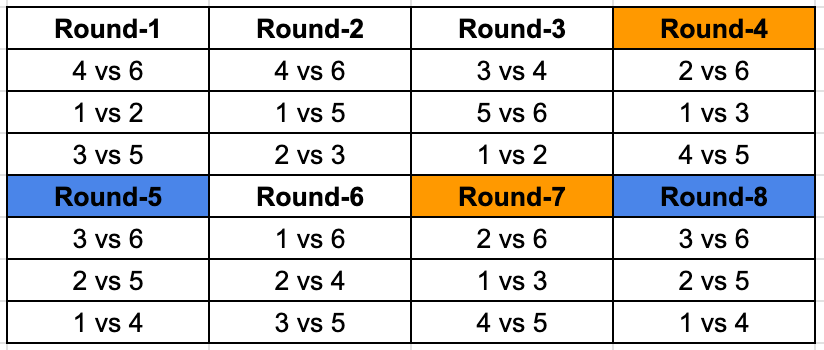
This is the final table.
The tournament will have 8 rounds.
Q2: What is the number of the team that played Team 1 in Round 5?
 View Answer
View Answer 
Ans: 4
We are told that there are six teams, that are divided into two groups.
Teams in the same group will play each other only once, and teams in different group will play each other twice.
Calculating the combinations, there is going to be 3C2 games among teams in the same group among them, and since there is two groups, total such games will be 6.
Now, teams in different group play each other twice. Calculating the combinations for this,
From the first group, a team can be chosen in three ways, and from the second group, a team can be chosen in three ways. Total ways two teams from different groups can play each other is 3x3 which is 9. And since they play each other twice, that is 9+9 games of this combination.
Total number of games is 18+6=24
It is given that each team plays one game in each round, that means there is going to be 3 matchups in each round. And given, there is 24 games to played in this format, the number of rounds will be 24/3=8
The tournament will have 8 rounds.
Now that we know there are going to be 8 rounds in the tournament, let us identify the teams in a particular group, that will help us build the matchups.
We are told that Round 8 teams from different groups play each other, and Teams 1 and 5 play only once. This means, 1 and 5 have to be on the same group. It is also told that 4 and 6 play each other twice, that means 4 and 6 have to be in different groups. Looking at the matches from Round 8 that is given to us, 3 played 6 and 2 played 5. We already know 1 and 5 are in the same group, so 2 must be in the other group. Among 3 and 6, if we were to place 3 in the group with 1 and 5, 4 and 6 would have to be in the same group, which is not possible, hence 6 is with 1 and 5, giving us the final combination of groups.

Now, using the given information to build the matchups for the 8 rounds.
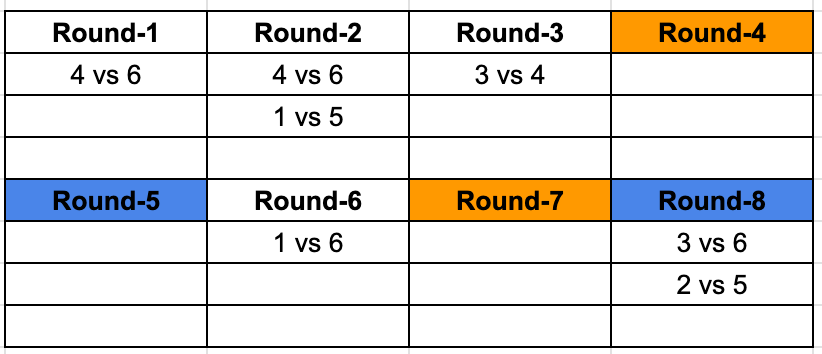 Rounds marked with the same colour represent the fact that the matchups are identical. Now we know that each team plays a game in each round, we know 2 out of the 3 matches for Round 2 and 8, and we can identify the third matchups as well. Giving us this resulting table.
Rounds marked with the same colour represent the fact that the matchups are identical. Now we know that each team plays a game in each round, we know 2 out of the 3 matches for Round 2 and 8, and we can identify the third matchups as well. Giving us this resulting table.
 We are told that Round 4 and 7 are identical, that means they are the matchups between teams from two different groups,
We are told that Round 4 and 7 are identical, that means they are the matchups between teams from two different groups,
We look at the matchups that are remaining among the 6 teams where both the games are left to play.
Right away we identify that 6 is yet to play 2 twice and 5 once. We are looking for teams playing twice, so both Round 4 and 7 has a matchups between 2 and 6. This means 6 will play 5 in Round 3 and using that we can identify the third matchup in Round 3 as well.
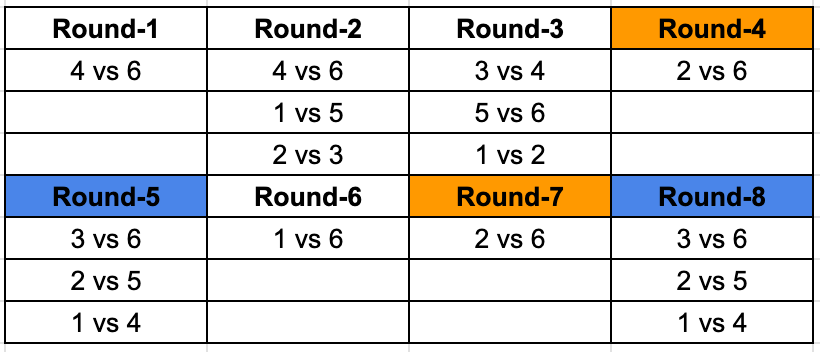 Now, we can identify that 1 is yet to play 3 both the times, 2 once. And we are looking for teams playing each other twice, so we can fill in the remaining values in the table as well.
Now, we can identify that 1 is yet to play 3 both the times, 2 once. And we are looking for teams playing each other twice, so we can fill in the remaining values in the table as well.
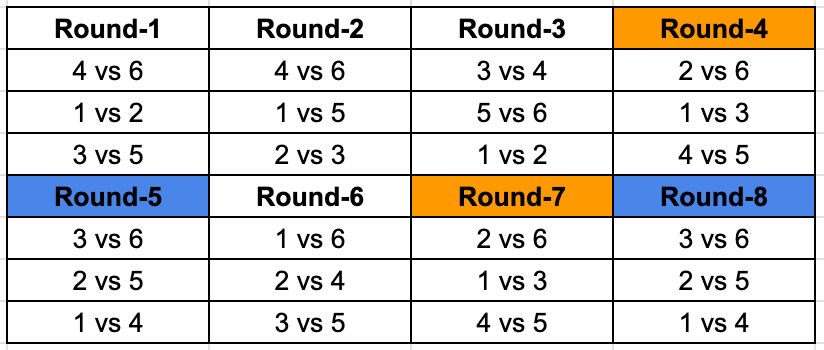 This is the final table.
This is the final table.
The team that played Team 1 in Round 5 is 4.
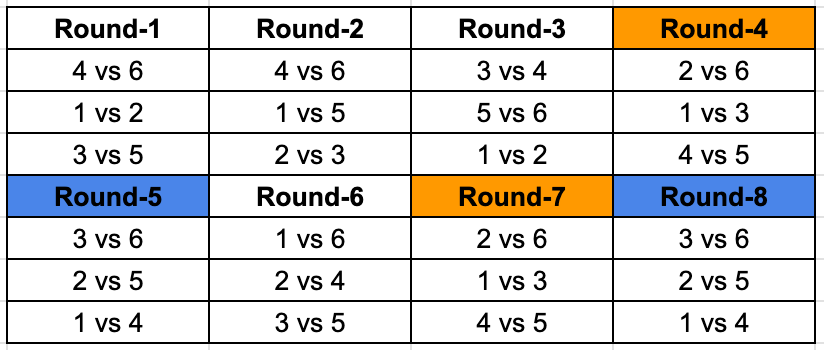
Q3: Which team among the teams numbered 2, 3, 4, and 5 was not part of the same group?
 View Answer
View Answer 
Ans: 5
We are told that there are six teams, that are divided into two groups.
Teams in the same group will play each other only once, and teams in different group will play each other twice.
Calculating the combinations, there is going to be 3C2 games among teams in the same group among them, and since there is two groups, total such games will be 6.
Now, teams in different group play each other twice. Calculating the combinations for this,
From the first group, a team can be chosen in three ways, and from the second group, a team can be chosen in three ways. Total ways two teams from different groups can play each other is 3x3 which is 9. And since they play each other twice, that is 9+9 games of this combination.
Total number of games is 18+6=24
It is given that each team plays one game in each round, that means there is going to be 3 matchups in each round. And given, there is 24 games to played in this format, the number of rounds will be 24/3=8
The tournament will have 8 rounds.
Now that we know there are going to be 8 rounds in the tournament, let us identify the teams in a particular group, that will help us build the matchups.
We are told that Round 8 teams from different groups play each other, and Teams 1 and 5 play only once. This means, 1 and 5 have to be on the same group. It is also told that 4 and 6 play each other twice, that means 4 and 6 have to be in different groups. Looking at the matches from Round 8 that is given to us, 3 played 6 and 2 played 5. We already know 1 and 5 are in the same group, so 2 must be in the other group. Among 3 and 6, if we were to place 3 in the group with 1 and 5, 4 and 6 would have to be in the same group, which is not possible, hence 6 is with 1 and 5, giving us the final combination of groups.
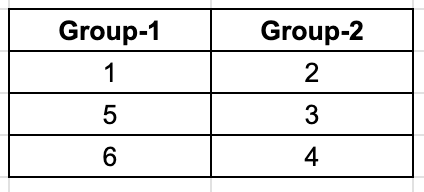 Now, using the given information to build the matchups for the 8 rounds.
Now, using the given information to build the matchups for the 8 rounds.
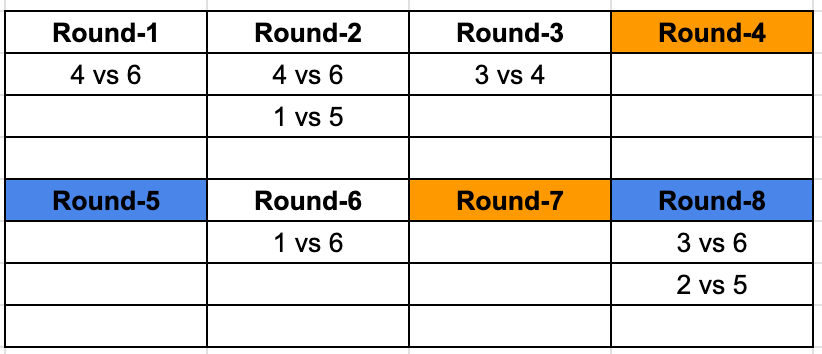 Rounds marked with the same colour represent the fact that the matchups are identical. Now we know that each team plays a game in each round, we know 2 out of the 3 matches for Round 2 and 8, and we can identify the third matchups as well. Giving us this resulting table.
Rounds marked with the same colour represent the fact that the matchups are identical. Now we know that each team plays a game in each round, we know 2 out of the 3 matches for Round 2 and 8, and we can identify the third matchups as well. Giving us this resulting table.
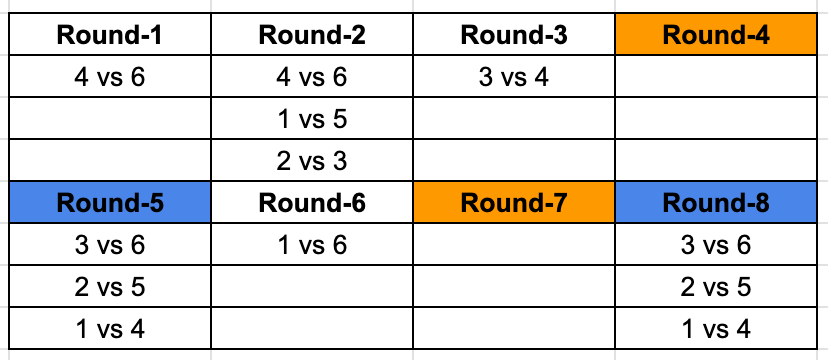 We are told that Round 4 and 7 are identical, that means they are the matchups between teams from two different groups,We look at the matchups that are remaining among the 6 teams where both the games are left to play.Right away we identify that 6 is yet to play 2 twice and 5 once. We are looking for teams playing twice, so both Round 4 and 7 has a matchups between 2 and 6. This means 6 will play 5 in Round 3 and using that we can identify the third matchup in Round 3 as well.
We are told that Round 4 and 7 are identical, that means they are the matchups between teams from two different groups,We look at the matchups that are remaining among the 6 teams where both the games are left to play.Right away we identify that 6 is yet to play 2 twice and 5 once. We are looking for teams playing twice, so both Round 4 and 7 has a matchups between 2 and 6. This means 6 will play 5 in Round 3 and using that we can identify the third matchup in Round 3 as well.
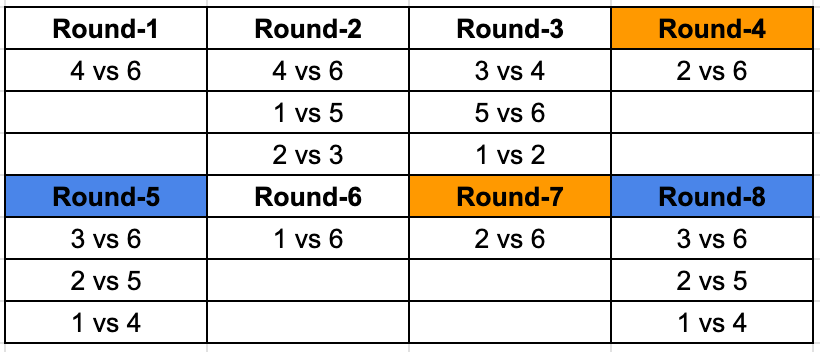 Now, we can identify that 1 is yet to play 3 both the times, 2 once. And we are looking for teams playing each other twice, so we can fill in the remaining values in the table as well.
Now, we can identify that 1 is yet to play 3 both the times, 2 once. And we are looking for teams playing each other twice, so we can fill in the remaining values in the table as well.
 This is the final table.
This is the final table.
2, 3 and 4 were part of the same group. 5 is the answer.
Q4: What is the number of the team that played Team 1 in Round 7?
 View Answer
View Answer 
Ans: 3
We are told that there are six teams, that are divided into two groups.
Teams in the same group will play each other only once, and teams in different group will play each other twice.
Calculating the combinations, there is going to be 3C2 games among teams in the same group among them, and since there is two groups, total such games will be 6.
Now, teams in different group play each other twice. Calculating the combinations for this,
From the first group, a team can be chosen in three ways, and from the second group, a team can be chosen in three ways. Total ways two teams from different groups can play each other is 3x3 which is 9. And since they play each other twice, that is 9+9 games of this combination.
Total number of games is 18+6=24
It is given that each team plays one game in each round, that means there is going to be 3 matchups in each round. And given, there is 24 games to played in this format, the number of rounds will be 24/3=8
The tournament will have 8 rounds.
Now that we know there are going to be 8 rounds in the tournament, let us identify the teams in a particular group, that will help us build the matchups.
We are told that Round 8 teams from different groups play each other, and Teams 1 and 5 play only once. This means, 1 and 5 have to be on the same group. It is also told that 4 and 6 play each other twice, that means 4 and 6 have to be in different groups. Looking at the matches from Round 8 that is given to us, 3 played 6 and 2 played 5. We already know 1 and 5 are in the same group, so 2 must be in the other group. Among 3 and 6, if we were to place 3 in the group with 1 and 5, 4 and 6 would have to be in the same group, which is not possible, hence 6 is with 1 and 5, giving us the final combination of groups.
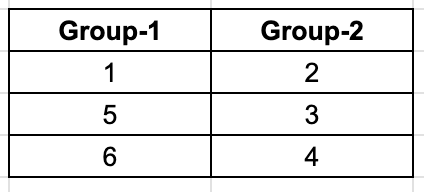 Now, using the given information to build the matchups for the 8 rounds.
Now, using the given information to build the matchups for the 8 rounds.
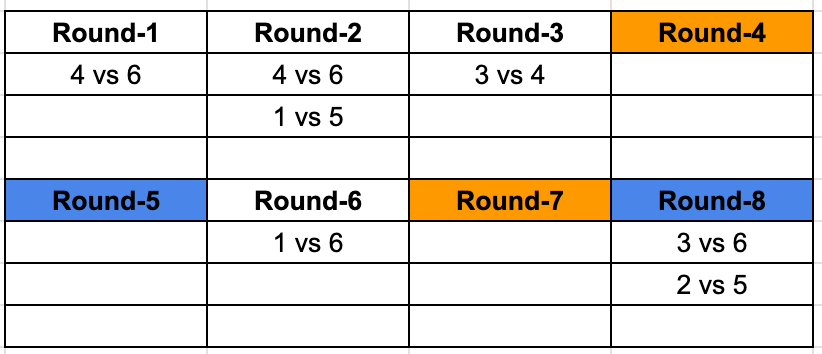 Rounds marked with the same colour represent the fact that the matchups are identical. Now we know that each team plays a game in each round, we know 2 out of the 3 matches for Round 2 and 8, and we can identify the third matchups as well. Giving us this resulting table.
Rounds marked with the same colour represent the fact that the matchups are identical. Now we know that each team plays a game in each round, we know 2 out of the 3 matches for Round 2 and 8, and we can identify the third matchups as well. Giving us this resulting table.
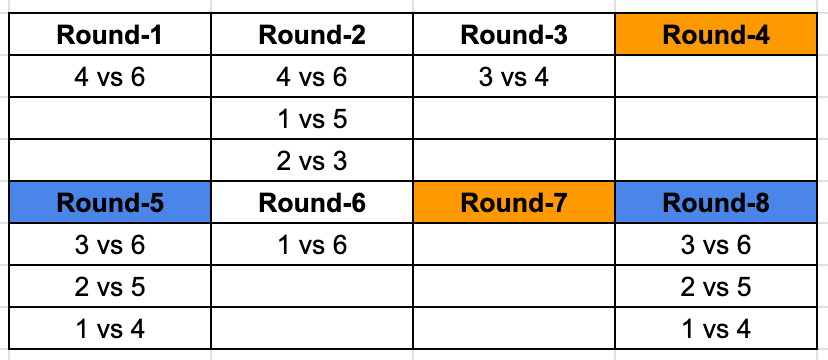 We are told that Round 4 and 7 are identical, that means they are the matchups between teams from two different groups,
We are told that Round 4 and 7 are identical, that means they are the matchups between teams from two different groups,
We look at the matchups that are remaining among the 6 teams where both the games are left to play.
Right away we identify that 6 is yet to play 2 twice and 5 once. We are looking for teams playing twice, so both Round 4 and 7 has a matchups between 2 and 6. This means 6 will play 5 in Round 3 and using that we can identify the third matchup in Round 3 as well.
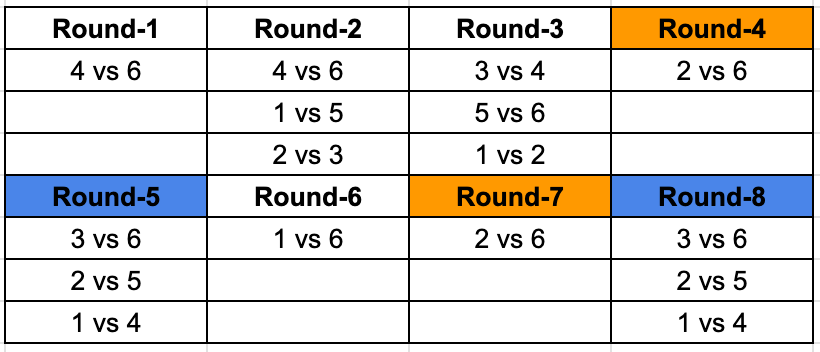 Now, we can identify that 1 is yet to play 3 both the times, 2 once. And we are looking for teams playing each other twice, so we can fill in the remaining values in the table as well.
Now, we can identify that 1 is yet to play 3 both the times, 2 once. And we are looking for teams playing each other twice, so we can fill in the remaining values in the table as well.
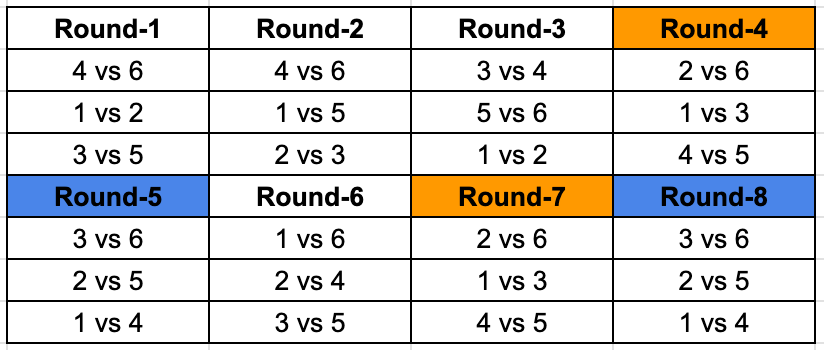 This is the final table.
This is the final table.
The team that played Team 1 in Round 7 is 3.
Q5: What is the number of the team that played Team 6 in Round 3?
 View Answer
View Answer 
Ans: 5
We are told that there are six teams, that are divided into two groups.
Teams in the same group will play each other only once, and teams in different group will play each other twice.
Calculating the combinations, there is going to be 3C2 games among teams in the same group among them, and since there is two groups, total such games will be 6.
Now, teams in different group play each other twice. Calculating the combinations for this,
From the first group, a team can be chosen in three ways, and from the second group, a team can be chosen in three ways. Total ways two teams from different groups can play each other is 3x3 which is 9. And since they play each other twice, that is 9+9 games of this combination.
Total number of games is 18+6=24
It is given that each team plays one game in each round, that means there is going to be 3 matchups in each round. And given, there is 24 games to played in this format, the number of rounds will be 24/3=8
The tournament will have 8 rounds.
Now that we know there are going to be 8 rounds in the tournament, let us identify the teams in a particular group, that will help us build the matchups.
We are told that Round 8 teams from different groups play each other, and Teams 1 and 5 play only once. This means, 1 and 5 have to be on the same group. It is also told that 4 and 6 play each other twice, that means 4 and 6 have to be in different groups. Looking at the matches from Round 8 that is given to us, 3 played 6 and 2 played 5. We already know 1 and 5 are in the same group, so 2 must be in the other group. Among 3 and 6, if we were to place 3 in the group with 1 and 5, 4 and 6 would have to be in the same group, which is not possible, hence 6 is with 1 and 5, giving us the final combination of groups.
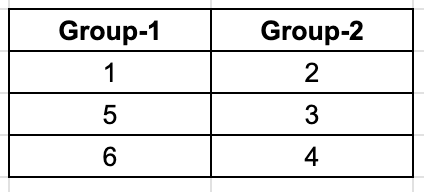 Now, using the given information to build the matchups for the 8 rounds.
Now, using the given information to build the matchups for the 8 rounds.
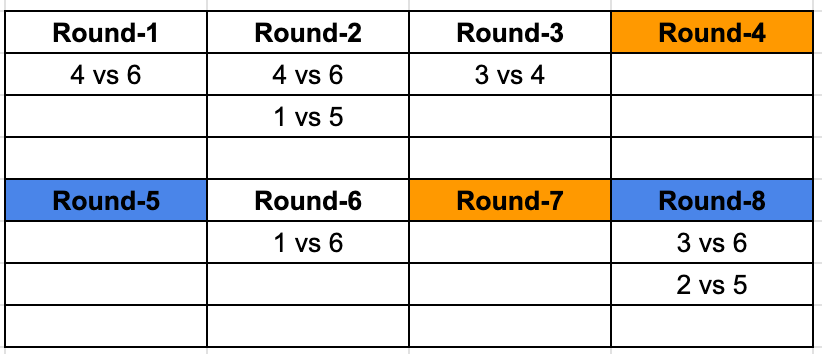 Rounds marked with the same colour represent the fact that the matchups are identical. Now we know that each team plays a game in each round, we know 2 out of the 3 matches for Round 2 and 8, and we can identify the third matchups as well. Giving us this resulting table.
Rounds marked with the same colour represent the fact that the matchups are identical. Now we know that each team plays a game in each round, we know 2 out of the 3 matches for Round 2 and 8, and we can identify the third matchups as well. Giving us this resulting table.
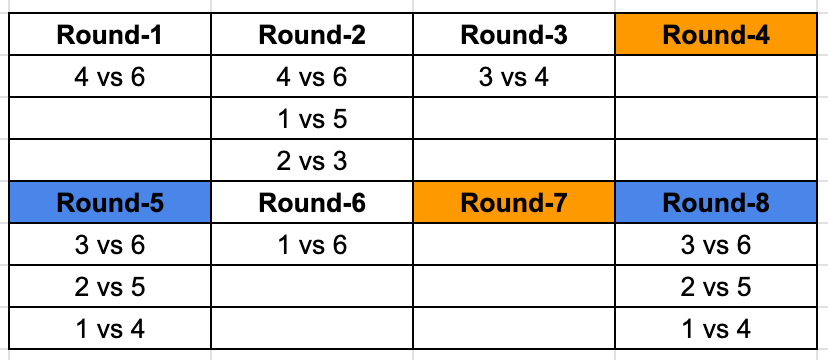 We are told that Round 4 and 7 are identical, that means they are the matchups between teams from two different groups,
We are told that Round 4 and 7 are identical, that means they are the matchups between teams from two different groups,
We look at the matchups that are remaining among the 6 teams where both the games are left to play.
Right away we identify that 6 is yet to play 2 twice and 5 once. We are looking for teams playing twice, so both Round 4 and 7 has a matchups between 2 and 6. This means 6 will play 5 in Round 3 and using that we can identify the third matchup in Round 3 as well.
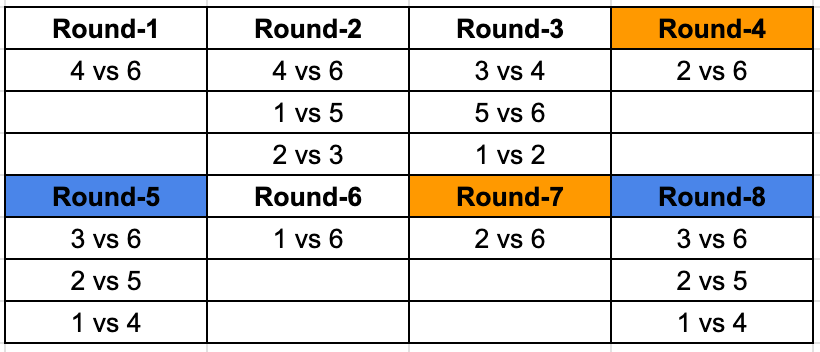 Now, we can identify that 1 is yet to play 3 both the times, 2 once. And we are looking for teams playing each other twice, so we can fill in the remaining values in the table as well.
Now, we can identify that 1 is yet to play 3 both the times, 2 once. And we are looking for teams playing each other twice, so we can fill in the remaining values in the table as well.
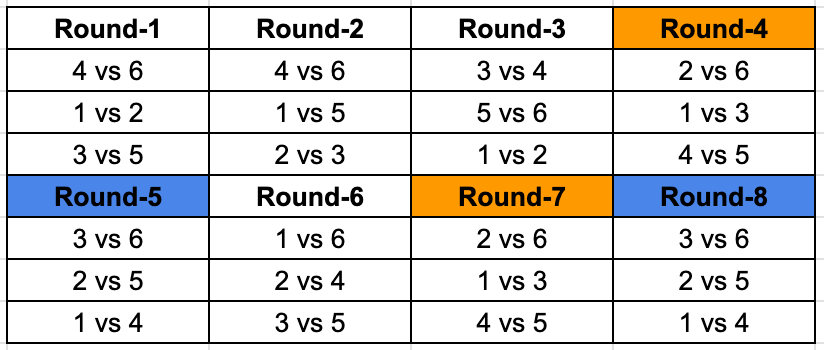 This is the final table.
This is the final table.
Team that played Team 6 in Round 3 was Team 5.
Que 2: Instructions for Set 2 (2023)
Pulak, Qasim, Ritesh, and Suresh participated in a tournament comprising of eight rounds. In each round, they formed two pairs, with each of them being in exactly one pair. The only restriction in the pairing was that the pairs would change in successive rounds. For example, if Pulak formed a pair with Qasim in the first round, then he would have to form a pair with Ritesh or Suresh in the second round. He would be free to pair with Qasim again in the third round. In each round, each pair decided whether to play the game in that round or not. If they decided not to play, then no money was exchanged between them. If they decided to play, they had to bet either ₹1 or ₹2 in that round. For example, if they chose to bet ₹2, then the player winning the game got ₹2 from the one losing the game.
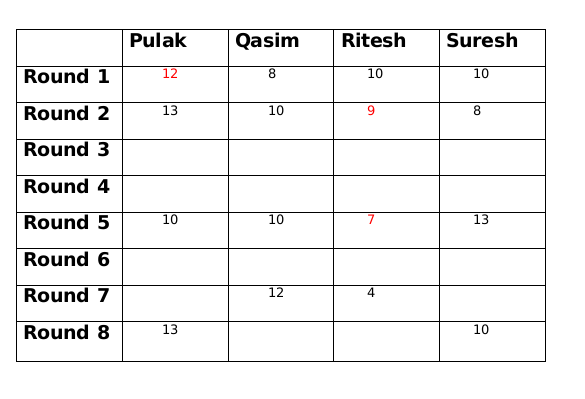
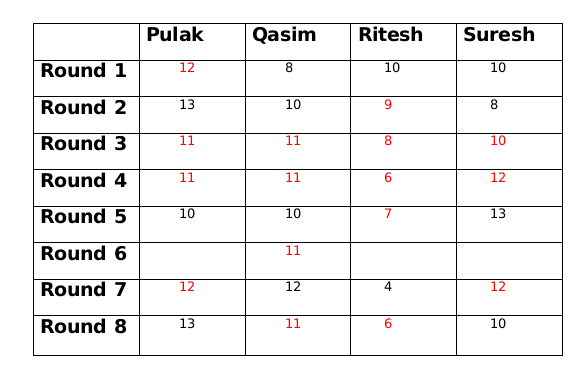
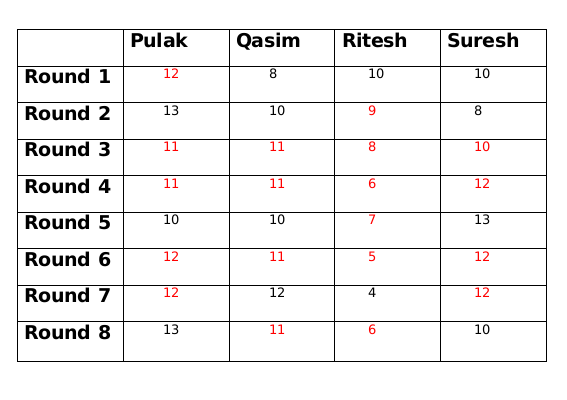
At the beginning of the tournament, the players had ₹10 each. The following table shows partial information about the amounts that the players had at the end of each of the eightrounds. It shows every time a player had ₹10 at the end of a round, as well as every time, at the end of a round, a player had either the minimum or the maximum amount that he would have had across the eight rounds. For example, Suresh had ₹10 at the end of Rounds 1, 3 and 8 and not after any of the other rounds. The maximum amount that he had at the end of any round was ₹13 (at the end of Round 5), and the minimum amount he had at the end of any round was ₹8 (at the end of Round 2). At the end of all other rounds, he must have had either ₹9, ₹11, or ₹12.
It was also known that Pulak and Qasim had the same amount of money with them at the end of Round 4.

Q1: What BEST can be said about the amount of money that Pulak had with him at the end of Round 6?
 View Answer
View Answer 
Ans: Exactly ₹12
Its given that the table shows every time a player had ₹10 at the end of a round, as well as every time, at the end of a round, a player had either the minimum or the maximum amount that he would have had across the eight rounds, which means that in Pulak's column the numbers possible are 11 or 12 only, similarly in Qasim's column numbers possible are only 9 or 11 only, similarly in Ritesh's column numbers possible are 5,6,7,8 or 9 only and in Suresh's column numbers possible are 9,11 or 12 only.
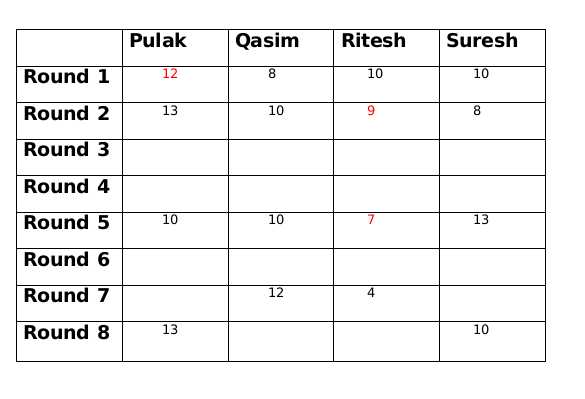
Everyone started with 10 rupees and the total amount,i.e., 40 in each round remains the same. So we get the following table
 We are given that at the end of 4th round both Pulak and Qasim had the same amount with them and that amount possible is only 11.
We are given that at the end of 4th round both Pulak and Qasim had the same amount with them and that amount possible is only 11.
As per the information given in the set the only possible amount with Qasim at the end of round 6 is 11.
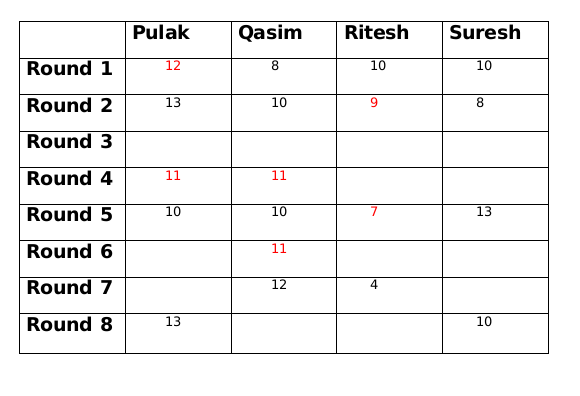
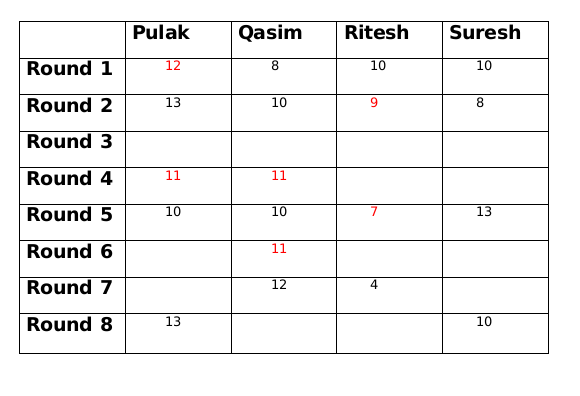 Amounts with Pulak and Qasim at the end of round 5 is decreased by 1 from the amounts which they had at the end of round 4, since the total amount will be same at the end of every round, so amounts with Ritesh and Suresh at the end of round 5 is increased by 1 from the amounts which they had at the end of round 4.
Amounts with Pulak and Qasim at the end of round 5 is decreased by 1 from the amounts which they had at the end of round 4, since the total amount will be same at the end of every round, so amounts with Ritesh and Suresh at the end of round 5 is increased by 1 from the amounts which they had at the end of round 4.
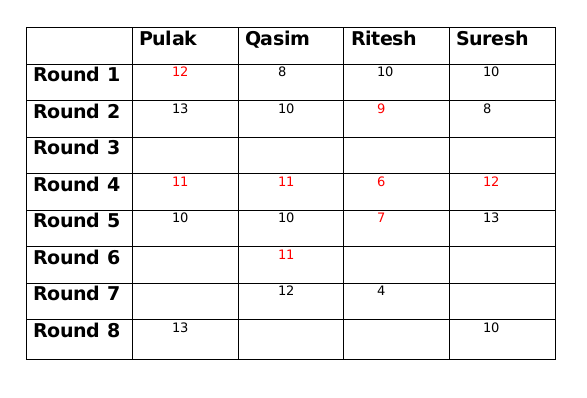 Amount with Suresh at the end of round 2 is 8 and at the end of round 4 is 12, therefore, amount with Suresh at the end of round 3 is 10.
Amount with Suresh at the end of round 2 is 8 and at the end of round 4 is 12, therefore, amount with Suresh at the end of round 3 is 10.
Amount with Qasim at the end of round 3 is either 9 or 11. If the amount is 9 then either amount with Ritesh has to be 10 or amount with Pulak has to to be 14, both of which is not possible. Therefore, amount with Qasim at the end of round 3 is 11.
 Now Qasim has the same amount at the end of round 3 and round 4 so there must be another person whose amount is also same at the end of round 3 and round 4. This person can only be Pulak. So at the end of round 3 Pulak has 11 rupees and Ritesh has 8 rupees.
Now Qasim has the same amount at the end of round 3 and round 4 so there must be another person whose amount is also same at the end of round 3 and round 4. This person can only be Pulak. So at the end of round 3 Pulak has 11 rupees and Ritesh has 8 rupees.
The only possible amount with Qasim at the end of round 8 can be 11 and therefore the amount at the end of round 8 with Ritesh will be 6.
 The amount with Ritesh at the end of round 8 is 2 more than the amount with him at the end of round 7, so the amount with either Pulak or Suresh at the end of round 7 has to be 2 more than the amount at the end of round 8. This is only possible for Suresh who must have 12 rupees at the end of round 7 as Pulak cannot have rupees 15 at the end of round 7.
The amount with Ritesh at the end of round 8 is 2 more than the amount with him at the end of round 7, so the amount with either Pulak or Suresh at the end of round 7 has to be 2 more than the amount at the end of round 8. This is only possible for Suresh who must have 12 rupees at the end of round 7 as Pulak cannot have rupees 15 at the end of round 7.
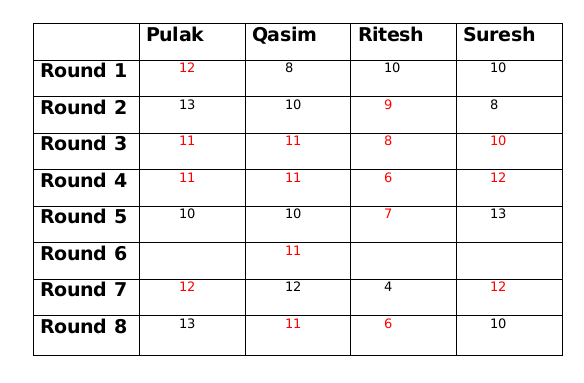 The amount with Qasim at the end of round 7 is 1 more than the amount with him at the end of round 6. So there must be another person whose amount at the end of round 7 is 1 less than the amount him at the end of round 6. This only possible person can be Ritesh. So amount with Ritesh at the end of round 6 will be 5.
The amount with Qasim at the end of round 7 is 1 more than the amount with him at the end of round 6. So there must be another person whose amount at the end of round 7 is 1 less than the amount him at the end of round 6. This only possible person can be Ritesh. So amount with Ritesh at the end of round 6 will be 5.
If the amount with Suresh at the end of round 6 is 11 then the amount with Pulak at the end of round 6 will be 13 which is not possible. Therefore the amount with Suresh at the end of round 6 is 12 and the amount with Pulak at the end of round 6 is 12.
Q2: How much money (in ₹) did Ritesh have at the end of Round 4?
 View Answer
View Answer 
Ans: 6
Its given that the table shows every time a player had ₹10 at the end of a round, as well as every time, at the end of a round, a player had either the minimum or the maximum amount that he would have had across the eight rounds, which means that in Pulak's column the numbers possible are 11 or 12 only, similarly in Qasim's column numbers possible are only 9 or 11 only, similarly in Ritesh's column numbers possible are 5,6,7,8 or 9 only and in Suresh's column numbers possible are 9,11 or 12 only.
Everyone started with 10 rupees and the total amount,i.e., 40 in each round remains the same. So we get the following table
 We are given that at the end of 4th round both Pulak and Qasim had the same amount with them and that amount possible is only 11.
We are given that at the end of 4th round both Pulak and Qasim had the same amount with them and that amount possible is only 11.
As per the information given in the set the only possible amount with Qasim at the end of round 6 is 11.
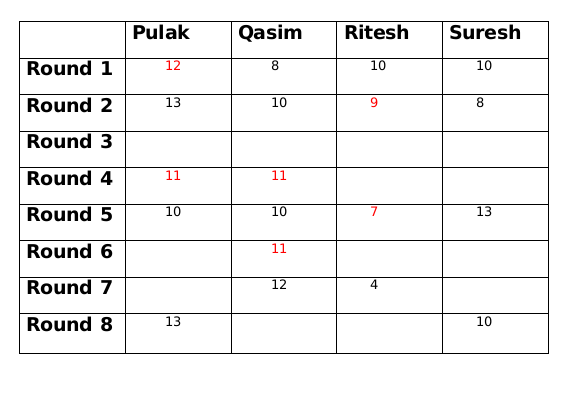 Amounts with Pulak and Qasim at the end of round 5 is decreased by 1 from the amounts which they had at the end of round 4, since the total amount will be same at the end of every round, so amounts with Ritesh and Suresh at the end of round 5 is increased by 1 from the amounts which they had at the end of round 4.
Amounts with Pulak and Qasim at the end of round 5 is decreased by 1 from the amounts which they had at the end of round 4, since the total amount will be same at the end of every round, so amounts with Ritesh and Suresh at the end of round 5 is increased by 1 from the amounts which they had at the end of round 4.
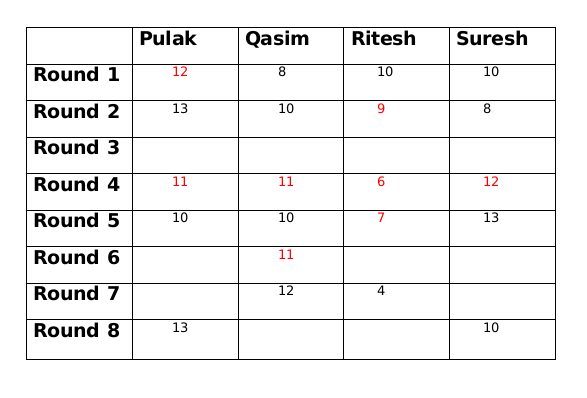 Amount with Suresh at the end of round 2 is 8 and at the end of round 4 is 12, therefore, amount with Suresh at the end of round 3 is 10.
Amount with Suresh at the end of round 2 is 8 and at the end of round 4 is 12, therefore, amount with Suresh at the end of round 3 is 10.
Amount with Qasim at the end of round 3 is either 9 or 11. If the amount is 9 then either amount with Ritesh has to be 10 or amount with Pulak has to to be 14, both of which is not possible. Therefore, amount with Qasim at the end of round 3 is 11.
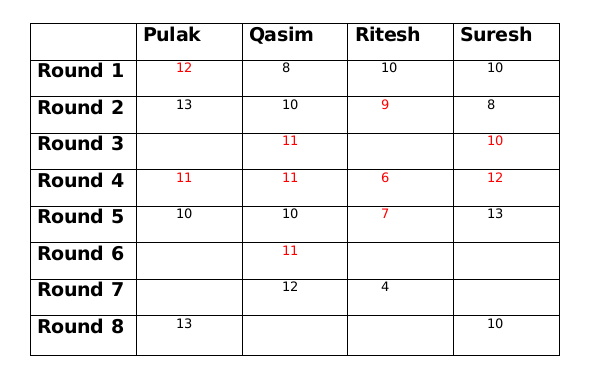 Now Qasim has the same amount at the end of round 3 and round 4 so there must be another person whose amount is also same at the end of round 3 and round 4. This person can only be Pulak. So at the end of round 3 Pulak has 11 rupees and Ritesh has 8 rupees.
Now Qasim has the same amount at the end of round 3 and round 4 so there must be another person whose amount is also same at the end of round 3 and round 4. This person can only be Pulak. So at the end of round 3 Pulak has 11 rupees and Ritesh has 8 rupees.
The only possible amount with Qasim at the end of round 8 can be 11 and therefore the amount at the end of round 8 with Ritesh will be 6.
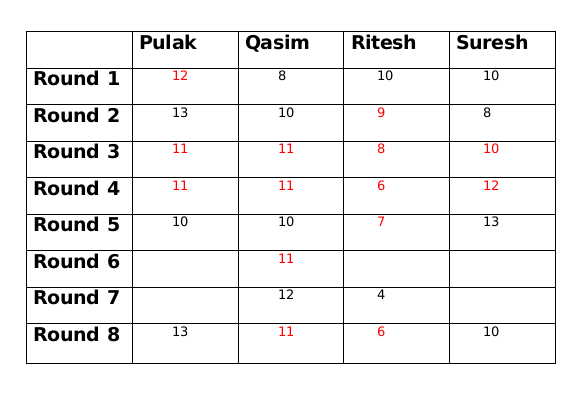 The amount with Ritesh at the end of round 8 is 2 more than the amount with him at the end of round 7, so the amount with either Pulak or Suresh at the end of round 7 has to be 2 more than the amount at the end of round 8. This is only possible for Suresh who must have 12 rupees at the end of round 7 as Pulak cannot have rupees 15 at the end of round 7.
The amount with Ritesh at the end of round 8 is 2 more than the amount with him at the end of round 7, so the amount with either Pulak or Suresh at the end of round 7 has to be 2 more than the amount at the end of round 8. This is only possible for Suresh who must have 12 rupees at the end of round 7 as Pulak cannot have rupees 15 at the end of round 7.
 The amount with Qasim at the end of round 7 is 1 more than the amount with him at the end of round 6. So there must be another person whose amount at the end of round 7 is 1 less than the amount him at the end of round 6. This only possible person can be Ritesh. So amount with Ritesh at the end of round 6 will be 5.
The amount with Qasim at the end of round 7 is 1 more than the amount with him at the end of round 6. So there must be another person whose amount at the end of round 7 is 1 less than the amount him at the end of round 6. This only possible person can be Ritesh. So amount with Ritesh at the end of round 6 will be 5.
If the amount with Suresh at the end of round 6 is 11 then the amount with Pulak at the end of round 6 will be 13 which is not possible. Therefore the amount with Suresh at the end of round 6 is 12 and the amount with Pulak at the end of round 6 is 12.
Q3: How many games were played with a bet of ₹2?
 View Answer
View Answer 
Ans: 6
Its given that the table shows every time a player had ₹10 at the end of a round, as well as every time, at the end of a round, a player had either the minimum or the maximum amount that he would have had across the eight rounds, which means that in Pulak's column the numbers possible are 11 or 12 only, similarly in Qasim's column numbers possible are only 9 or 11 only, similarly in Ritesh's column numbers possible are 5,6,7,8 or 9 only and in Suresh's column numbers possible are 9,11 or 12 only.
Everyone started with 10 rupees and the total amount,i.e., 40 in each round remains the same. So we get the following table
 We are given that at the end of 4th round both Pulak and Qasim had the same amount with them and that amount possible is only 11.
We are given that at the end of 4th round both Pulak and Qasim had the same amount with them and that amount possible is only 11.
As per the information given in the set the only possible amount with Qasim at the end of round 6 is 11.
 Amounts with Pulak and Qasim at the end of round 5 is decreased by 1 from the amounts which they had at the end of round 4, since the total amount will be same at the end of every round, so amounts with Ritesh and Suresh at the end of round 5 is increased by 1 from the amounts which they had at the end of round 4.
Amounts with Pulak and Qasim at the end of round 5 is decreased by 1 from the amounts which they had at the end of round 4, since the total amount will be same at the end of every round, so amounts with Ritesh and Suresh at the end of round 5 is increased by 1 from the amounts which they had at the end of round 4.
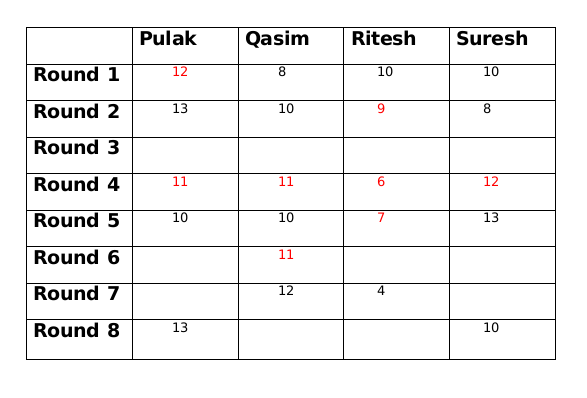 Amount with Suresh at the end of round 2 is 8 and at the end of round 4 is 12, therefore, amount with Suresh at the end of round 3 is 10.
Amount with Suresh at the end of round 2 is 8 and at the end of round 4 is 12, therefore, amount with Suresh at the end of round 3 is 10.
Amount with Qasim at the end of round 3 is either 9 or 11. If the amount is 9 then either amount with Ritesh has to be 10 or amount with Pulak has to to be 14, both of which is not possible. Therefore, amount with Qasim at the end of round 3 is 11.
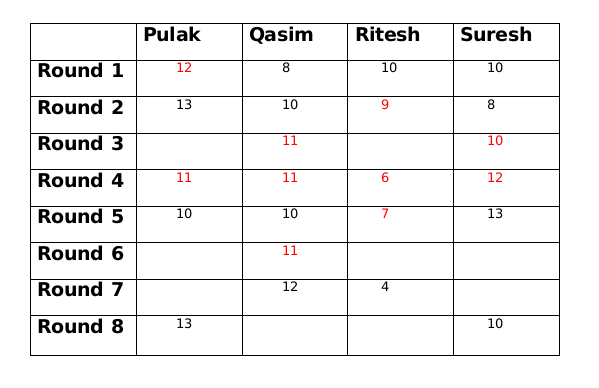 Now Qasim has the same amount at the end of round 3 and round 4 so there must be another person whose amount is also same at the end of round 3 and round 4. This person can only be Pulak. So at the end of round 3 Pulak has 11 rupees and Ritesh has 8 rupees.
Now Qasim has the same amount at the end of round 3 and round 4 so there must be another person whose amount is also same at the end of round 3 and round 4. This person can only be Pulak. So at the end of round 3 Pulak has 11 rupees and Ritesh has 8 rupees.
The only possible amount with Qasim at the end of round 8 can be 11 and therefore the amount at the end of round 8 with Ritesh will be 6.
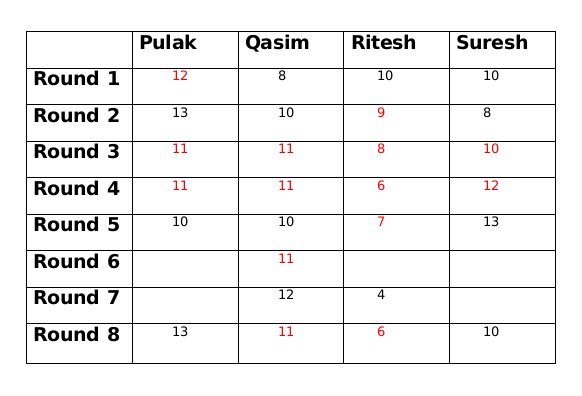 The amount with Ritesh at the end of round 8 is 2 more than the amount with him at the end of round 7, so the amount with either Pulak or Suresh at the end of round 7 has to be 2 more than the amount at the end of round 8. This is only possible for Suresh who must have 12 rupees at the end of round 7 as Pulak cannot have rupees 15 at the end of round 7.
The amount with Ritesh at the end of round 8 is 2 more than the amount with him at the end of round 7, so the amount with either Pulak or Suresh at the end of round 7 has to be 2 more than the amount at the end of round 8. This is only possible for Suresh who must have 12 rupees at the end of round 7 as Pulak cannot have rupees 15 at the end of round 7.
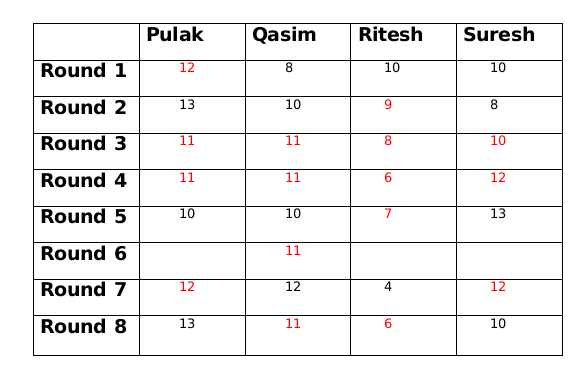 The amount with Qasim at the end of round 7 is 1 more than the amount with him at the end of round 6. So there must be another person whose amount at the end of round 7 is 1 less than the amount him at the end of round 6. This only possible person can be Ritesh. So amount with Ritesh at the end of round 6 will be 5.
The amount with Qasim at the end of round 7 is 1 more than the amount with him at the end of round 6. So there must be another person whose amount at the end of round 7 is 1 less than the amount him at the end of round 6. This only possible person can be Ritesh. So amount with Ritesh at the end of round 6 will be 5.
If the amount with Suresh at the end of round 6 is 11 then the amount with Pulak at the end of round 6 will be 13 which is not possible. Therefore the amount with Suresh at the end of round 6 is 12 and the amount with Pulak at the end of round 6 is 12.
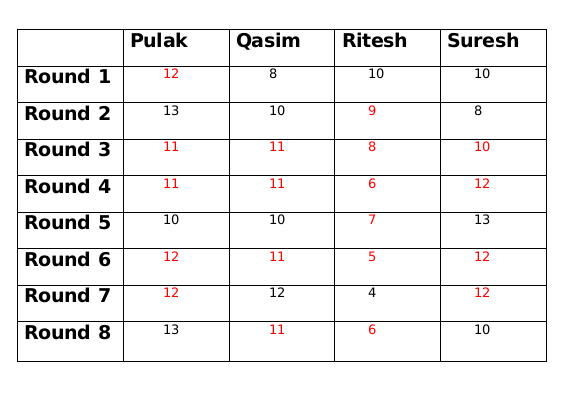
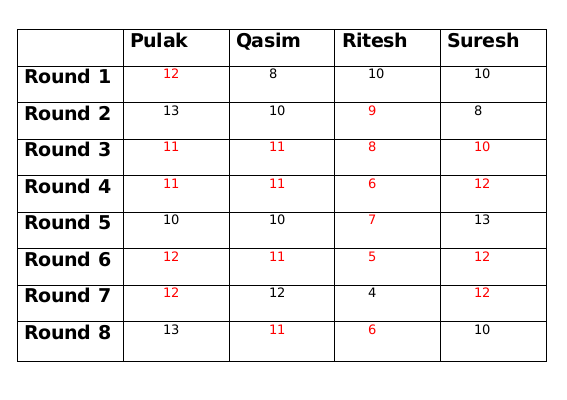
 The Games which had a bet of Rs.2 are as following
The Games which had a bet of Rs.2 are as following
Round 1 - Palak vs Qasim
Round 2 - Qasim vs Suresh
Round 3 - Palak vs Suresh
Round 4 - Ritesh vs Suresh
Round 5 - None
Round 6 - Palak vs Ritesh
Round 7 - None
Round 8 - Ritesh vs Suresh
Hence total number of games that were played with a bet of 2 is 6
|
77 videos|180 docs|96 tests
|
FAQs on TITA Based Questions: Games and Tournaments - Logical Reasoning (LR) and Data Interpretation (DI) - CAT
| 1. What are the different types of games and tournaments mentioned in the article? |  |
| 2. How can I prepare for a tournament based on the guidelines in the article? |  |
| 3. What strategies can be employed to succeed in tournament play? |  |
| 4. Are there any common mistakes to avoid in games and tournaments as per the article? |  |
| 5. What role does teamwork play in tournaments, especially in team-based games? |  |





















