TITA Based Questions : Arrangements and Puzzles | Logical Reasoning (LR) and Data Interpretation (DI) - CAT PDF Download
As TITA (Type In The Answer) based questions are gaining prominence in the CAT exam, it’s important to build accuracy without relying on options. The following are carefully curated TITA-based questions on the topic Arrangements and Puzzles to help you practice exact value-based problem solving.

Que 1: Instructions for Set 1 (2024)
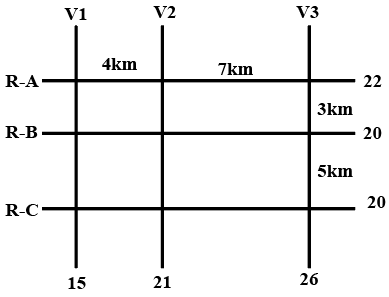
The figure below shows a network with three parallel roads represented by horizontal lines R-A, R-B, and R-C and another three parallel roads represented by vertical lines V1, V2, and V3. The figure also shows the distance (in km) between two adjacent intersections.Six ATMs are placed at six of the nine road intersections. Each ATM has a distinct integer cash requirement (in Rs. Lakhs), and the numbers at the end of each line in the figure indicate the total cash requirements of all ATMs placed on the corresponding road. For example, the total cash requirement of the ATM(s) placed on road R-A is Rs. 22 Lakhs.
The following additional information is known.
1. The ATMs with the minimum and maximum cash requirements of Rs. 7 Lakhs and Rs. 15 Lakhs are placed on the same road.
2. The road distance between the ATM with the second highest cash requirement and the ATM located at the intersection of R-C and V3 is 12 km.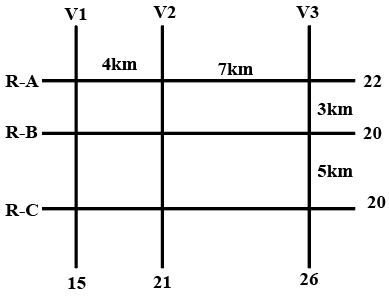 Q1: How many ATMs have cash requirements of Rs. 10 Lakhs or more?
Q1: How many ATMs have cash requirements of Rs. 10 Lakhs or more?
 View Answer
View Answer 
Ans: 3
This is the figure that has been given to us,
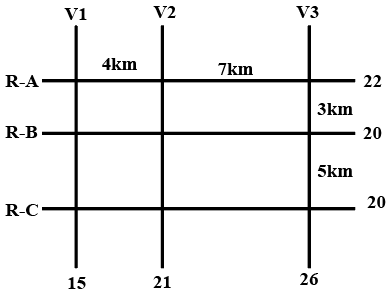 We are given the information that, out of the 9 intersections in the figure, 6 of them have ATMs. That means, 3 of these intersections are empty.
We are given the information that, out of the 9 intersections in the figure, 6 of them have ATMs. That means, 3 of these intersections are empty.
We are also told that, the ATMs with the highest and lowest capacity are on the same road, highest capacity being 15L and lowest being 7L.
This information not only gives us clues about the location of these two ATMs but also, now we know the upper and lower bounds for cash in the six ATMs with distinct cash.
Next piece of information that is given is that, road distance between the ATM with the second highest cashrequirement and the ATM located at the intersection of R-C and V3 is12 km. Since we can only traverse on the roads, from (RC, V3) we have to either traverse the 5km road or the 7km road. The only way it can add up to 12 is 5+7. That means, ATM with the second highest capacity is at (RB, V2).
Now, let us start arranging the ATM's.
We are told that 15 and 7 are on the same road. Since we are given the total capacities on the roads, we need to identify the roads with capacity higher or equal to 22.
There are only two possible choice, either RA or V3.
Looking at V3, we see that 15L ATM cannot come at (RB, V3) or (RC, V3) since the RB and RC capacity is 20, and the minimum ATM limit is 7L, if a 15L ATM is on a road with total capacity 20L, this is a situation that is not possible since there cannot be an ATM with 5L capacity.
The same is the case with the intersection (RA, V2). So, we can narrow down the fact that the 15L ATM has to either be at (RA, V1) or (RA, V3)
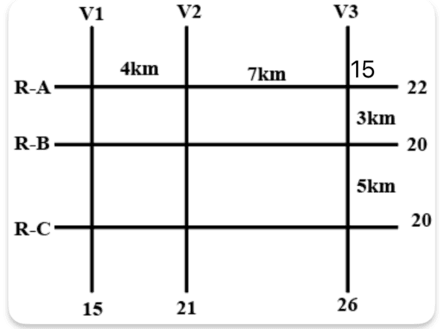
Case 1: 15L ATM is on the intersection (RA, V3)
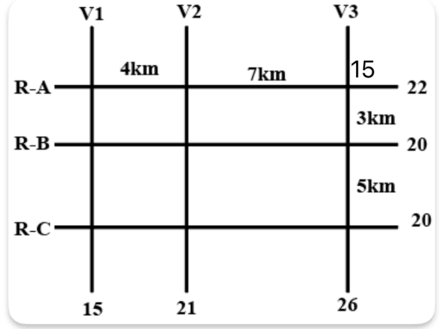 We see that, for V3 to add upto 26, there has to be an ATM with cash of 11L, there cannot be two ATM's since the minimum capacity is 7L.
We see that, for V3 to add upto 26, there has to be an ATM with cash of 11L, there cannot be two ATM's since the minimum capacity is 7L.
We can place the 11L ATM at (RB, V3) or (RC, V3), if we place them at either of these intersections, the remaining ATM has to have a capacity of 9L for the same reason. 9L cannot be at (RC, V1) or (RB, V1) since the total capacity of V1 is 15L and there cannot be an ATM with 6L. And it also cannot be at (RB, V2) since there is already an ATM with 11L that means the ATM with the second highest capacity cannot be 9. So that means 9L has to be at (RC, V2). And then filling in the rest of the numbers we get the final arrangement for Case-1.
 Case 2: When 15L is at (RA, V1)
Case 2: When 15L is at (RA, V1)
There can be no other ATM on V1 in this scenario, 7L ATM which is on RA cannot be on (RA, V2) considering the sum of the numbers on V2 is 21, and there cannot be 7+7 or a 14L ATM since the capacity of both RB and RC is 20. So, 7L has to be on V3, and since there cannot be a single ATM of 19L on V3, there has to be two other ATMs on V3 adding up to 19. Rearranging the numbers, we get the scenario for the second case.
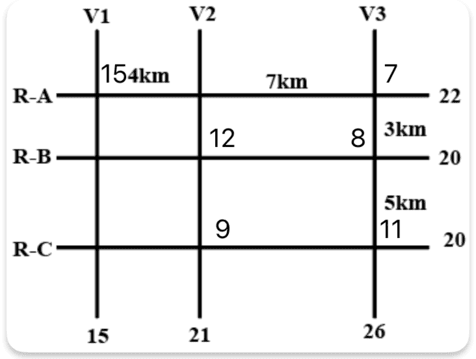 Using the two cases, we can answer the given questions.
Using the two cases, we can answer the given questions.
Three ATM's with 10L or more: 15L, 12L and 11L.
Answer is 3.
Q2: What is the number of ATMs whose locations and cash requirements can both be uniquely determined?
 View Answer
View Answer 
Ans: 3
This is the figure that has been given to us,
 We are given the information that, out of the 9 intersections in the figure, 6 of them have ATMs. That means, 3 of these intersections are empty.
We are given the information that, out of the 9 intersections in the figure, 6 of them have ATMs. That means, 3 of these intersections are empty.
We are also told that, the ATMs with the highest and lowest capacity are on the same road, highest capacity being 15L and lowest being 7L.
This information not only gives us clues about the location of these two ATMs but also, now we know the upper and lower bounds for cash in the six ATMs with distinct cash.
Next piece of information that is given is that, road distance between the ATM with the second highest cashrequirement and the ATM located at the intersection of R-C and V3 is12 km. Since we can only traverse on the roads, from (RC, V3) we have to either traverse the 5km road or the 7km road. The only way it can add up to 12 is 5+7. That means, ATM with the second highest capacity is at (RB, V2).
Now, let us start arranging the ATM's.
We are told that 15 and 7 are on the same road. Since we are given the total capacities on the roads, we need to identify the roads with capacity higher or equal to 22.
There are only two possible choice, either RA or V3.
Looking at V3, we see that 15L ATM cannot come at (RB, V3) or (RC, V3) since the RB and RC capacity is 20, and the minimum ATM limit is 7L, if a 15L ATM is on a road with total capacity 20L, this is a situation that is not possible since there cannot be an ATM with 5L capacity.
The same is the case with the intersection (RA, V2). So, we can narrow down the fact that the 15L ATM has to either be at (RA, V1) or (RA, V3)
Case 1: 15L ATM is on the intersection (RA, V3)
 We see that, for V3 to add upto 26, there has to be an ATM with cash of 11L, there cannot be two ATM's since the minimum capacity is 7L.
We see that, for V3 to add upto 26, there has to be an ATM with cash of 11L, there cannot be two ATM's since the minimum capacity is 7L.
We can place the 11L ATM at (RB, V3) or (RC, V3), if we place them at either of these intersections, the remaining ATM has to have a capacity of 9L for the same reason. 9L cannot be at (RC, V1) or (RB, V1) since the total capacity of V1 is 15L and there cannot be an ATM with 6L. And it also cannot be at (RB, V2) since there is already an ATM with 11L that means the ATM with the second highest capacity cannot be 9. So that means 9L has to be at (RC, V2). And then filling in the rest of the numbers we get the final arrangement for Case-1.
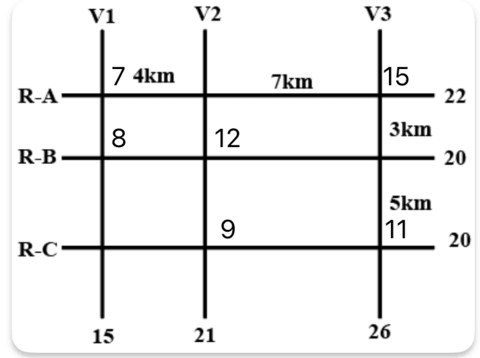 Case 2: When 15L is at (RA, V1)
Case 2: When 15L is at (RA, V1)
There can be no other ATM on V1 in this scenario, 7L ATM which is on RA cannot be on (RA, V2) considering the sum of the numbers on V2 is 21, and there cannot be 7+7 or a 14L ATM since the capacity of both RB and RC is 20. So, 7L has to be on V3, and since there cannot be a single ATM of 19L on V3, there has to be two other ATMs on V3 adding up to 19. Rearranging the numbers, we get the scenario for the second case.
 Using the two cases, we can answer the given questions.
Using the two cases, we can answer the given questions.
ATMs that can be uniquely determines are the ATMs with cash 9L, 11L and 12L.
Hence the answer is 3.
Que 2: Instructions for Set 2 (2023)
The schematic diagram below shows 12 rectangular houses in a housing complex. House numbers are mentioned in the rectangles representing the houses. The houses are located in six columns - Column-A through Column-F, and two rows - Row-1 and Row-2. The houses are divided into two blocks - Block XX and Block YY. The diagram also shows two roads, one passing in front of the houses in Row-2 and another between the two blocks.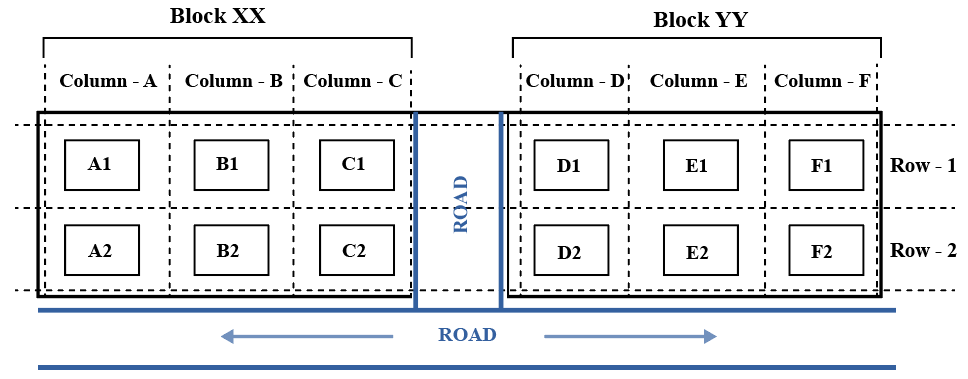
Some of the houses are occupied. The remaining ones are vacant and are the only ones available for sale.
The road adjacency value of a house is the number of its sides adjacent to a road. For example, the road adjacency values of C2, F2, and B1 are 2, 1, and 0, respectively. The neighbour count of a house is the number of sides of that house adjacent to occupied houses in the same block. For example, E1 and C1 can have the maximum possible neighbour counts of 3 and 2, respectively.
The base price of a vacant house is Rs. 10 lakhs if the house does not have a parking space, and Rs. 12 lakhs if it does. The quoted price (in lakhs of Rs.) of a vacant house is calculated as (base price) + 5 × (road adjacency value) + 3 × (neighbour count). The following information is also known.
1. The maximum quoted price of a house in Block XX is Rs. 24 lakhs. The minimum quoted price of a house in block YY is Rs. 15 lakhs, and one such house is in Column-E.
2. Row-1 has two occupied houses, one in each block.
3. Both houses in Column-E are vacant. Each of Column-D and Column-F has at least one occupied house.
4. There is only one house with parking space in Block YY.
Q1: How many houses are vacant in Block XX?
 View Answer
View Answer 
Ans: 3
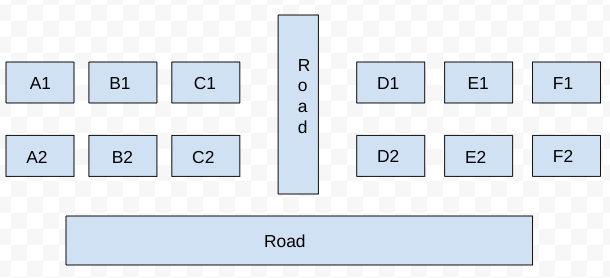 It is given that some of the houses are occupied. The remaining ones are vacant and are the only ones available for sale.
It is given that some of the houses are occupied. The remaining ones are vacant and are the only ones available for sale.
The base price of a vacant house is Rs. 10 lakhs if the house does not have a parking space, and Rs. 12 lakhs if it does. The quoted price (in lakhs of Rs.) of a vacant house is calculated as (base price) + 5 × (road adjacency value) + 3 × (neighbor count).
It is also known that the maximum quoted price of a house in Block XX is Rs. 24 lakhs
Hence, there can be two cases for the maximum quoted price of a house in block XX.
Case 1: House with parking space:
=> 12+5a+3b = 24 => 5a+3b = 12 ( a = road adjacency value, b= neighbor count)
The only value for which the equation satisfies is (a = 0, and b=4). But the value of b can't be 4 because the maximum neighbor count can be at most 3.
Hence, case 1 is invalid.
Case 2: House without parking space:
=> 10+5a+3b = 24 => 5a+3b = 14
=> (a, b) = (1, 3)
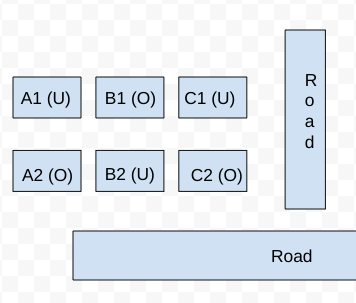
Hence, the house must have 3 neighbors and 1 road connected to it. Hence, the only possible case is B2. Therefore, the neighbor houses of B2, which are (B1, A2, and C2) are occupied.
It is known that Row 1 has two occupied houses, one in each block. Since B1 is already occupied, it implies A1, and C1 are vacant.
Hence, the configuration of block XX is given below: (Where U = Unoccupied/ Vacant, and U = Occupied)
 Now for block YY, we know that both houses in Column E are vacant. Each of Column-D and Column-F has at least one occupied house. There is only one house with parking space in Block YY.
Now for block YY, we know that both houses in Column E are vacant. Each of Column-D and Column-F has at least one occupied house. There is only one house with parking space in Block YY.
It is also known that the minimum quoted price of a house in block YY is Rs. 15 lakhs, and one such house is in Column E.
Case 1: The minimum quoted house is E2:
We know that the road adjacency of E2 is 1, hence we can calculate whether the house has parking space or not, and the neighbor count (b)
If the house has parking space, then: 12+5*1+3*b = 15 => 3b = -2 (which is not possible)
Hence, the house has no parking space => 10+5*1+3b = 15 => b = 0
b = 0 implies all the neighbor house of E2 is vacant, which are (E1, D2, and F2).
It is known that each of Column-D and Column-F has at least one occupied house, which implies D1, and F1 must be occupied.
But D1 and F1 can't be occupied together since the total number of occupied houses in Row 1 is 2 (one in each block).
Hence, This case is invalid.
Case 2: The minimum quoted house is E1:
We know that the road adjacency of E1 is 0, hence we can calculate whether the house has parking space or not, and the neighbor count (b).
i) If the house has no working space, then: 10+5*0+3b = 15 => b = 5/3 (this is not possible since b has to be an integer value)
Hence, the house has parking space => 12+5*0+3b = 15 => b = 1 => One neighbor house is occupied among D1 and F1.
Let's take the case of house D1 being occupied and F1 being empty. In that case, the value of house F1 would be 10(there is no parking space)+ (5*0) + (3*the number of neighbours)
Here, even if we take the number of neighbors to be 1, which is the maximum for F1 in this case, the value of F1 would be a maximum of 13. This is lower than the lowest-value house in block YY. Therefore, F1 cannot be empty.
Since F1 is occupied and we know that there is only one house occupied in row 1 of each block, D1 becomes unoccupied. D2 becomes occupied because it is given in the question that each of Column-D and Column-F has at least one occupied house.
Here, the value of D1 is 18 as D2 is occupied.
We do not know the status of house F2.
Therefore, the final diagram is given below:
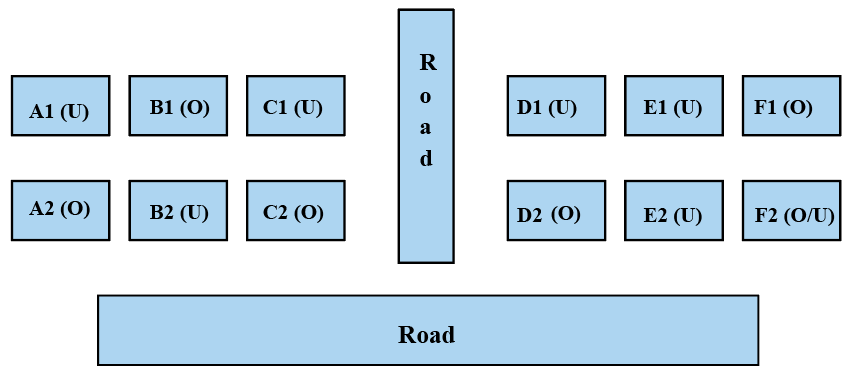 From the diagram, we can see that 3 houses are vacant in block XX.
From the diagram, we can see that 3 houses are vacant in block XX.
Q2: Which of the following houses is definitely occupied?
 View Answer
View Answer 
Ans: B1
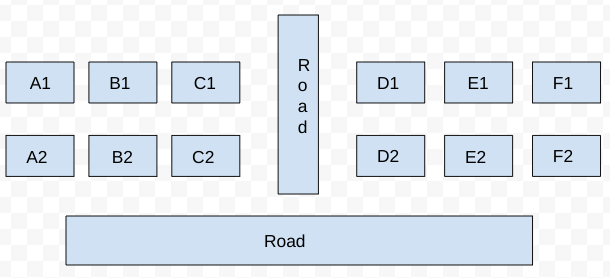 It is given that some of the houses are occupied. The remaining ones are vacant and are the only ones available for sale.
It is given that some of the houses are occupied. The remaining ones are vacant and are the only ones available for sale.
The base price of a vacant house is Rs. 10 lakhs if the house does not have a parking space, and Rs. 12 lakhs if it does. The quoted price (in lakhs of Rs.) of a vacant house is calculated as (base price) + 5 × (road adjacency value) + 3 × (neighbor count).
It is also known that the maximum quoted price of a house in Block XX is Rs. 24 lakhs
Hence, there can be two cases for the maximum quoted price of a house in block XX.
Case 1: House with parking space:
=> 12+5a+3b = 24 => 5a+3b = 12 ( a = road adjacency value, b= neighbor count)
The only value for which the equation satisfies is (a = 0, and b=4). But the value of b can't be 4 because the maximum neighbor count can be at most 3.
Hence, case 1 is invalid.
Case 2: House without parking space:
=> 10+5a+3b = 24 => 5a+3b = 14
=> (a, b) = (1, 3)
Hence, the house must have 3 neighbors and 1 road connected to it. Hence, the only possible case is B2. Therefore, the neighbor houses of B2, which are (B1, A2, and C2) are occupied.
It is known that Row 1 has two occupied houses, one in each block. Since B1 is already occupied, it implies A1, and C1 are vacant.
Hence, the configuration of block XX is given below: (Where U = Unoccupied/ Vacant, and U = Occupied)
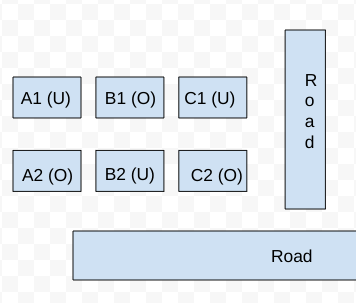 Now for block YY, we know that both houses in Column E are vacant. Each of Column-D and Column-F has at least one occupied house. There is only one house with parking space in Block YY.
Now for block YY, we know that both houses in Column E are vacant. Each of Column-D and Column-F has at least one occupied house. There is only one house with parking space in Block YY.
It is also known that the minimum quoted price of a house in block YY is Rs. 15 lakhs, and one such house is in Column E.
Case 1: The minimum quoted house is E2:
We know that the road adjacency of E2 is 1, hence we can calculate whether the house has parking space or not, and the neighbor count (b)
If the house has parking space, then: 12+5*1+3*b = 15 => 3b = -2 (which is not possible)
Hence, the house has no parking space => 10+5*1+3b = 15 => b = 0
b = 0 implies all the neighbor house of E2 is vacant, which are (E1, D2, and F2).
It is known that each of Column-D and Column-F has at least one occupied house, which implies D1, and F1 must be occupied.
But D1 and F1 can't be occupied together since the total number of occupied houses in Row 1 is 2 (one in each block).
Hence, This case is invalid.
Case 2: The minimum quoted house is E1:
We know that the road adjacency of E1 is 0, hence we can calculate whether the house has parking space or not, and the neighbor count (b).
i) If the house has no working space, then: 10+5*0+3b = 15 => b = 5/3 (this is not possible since b has to be an integer value)
Hence, the house has parking space => 12+5*0+3b = 15 => b = 1 => One neighbor house is occupied among D1 and F1.
Let's take the case of house D1 being occupied and F1 being empty. In that case, the value of house F1 would be 10(there is no parking space)+ (5*0) + (3*the number of neighbours)
Here, even if we take the number of neighbors to be 1, which is the maximum for F1 in this case, the value of F1 would be a maximum of 13. This is lower than the lowest-value house in block YY. Therefore, F1 cannot be empty.
Since F1 is occupied and we know that there is only one house occupied in row 1 of each block, D1 becomes unoccupied. D2 becomes occupied because it is given in the question that each of Column-D and Column-F has at least one occupied house.
Here, the value of D1 is 18 as D2 is occupied.
We do not know the status of house F2.
Therefore, the final diagram is given below:
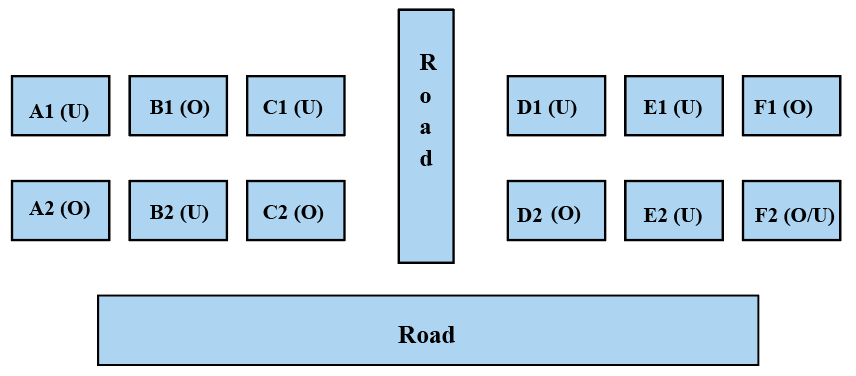 From the diagram, we can see that B1 and D2 are definitely occupied. The rest of the options are not definitely correct.
From the diagram, we can see that B1 and D2 are definitely occupied. The rest of the options are not definitely correct.
The correct options are both B and C.
Q3: What is the maximum possible quoted price (in lakhs of Rs.) for a vacant house in Column-E?
 View Answer
View Answer 
Ans: 21
 It is given that some of the houses are occupied. The remaining ones are vacant and are the only ones available for sale.The base price of a vacant house is Rs. 10 lakhs if the house does not have a parking space, and Rs. 12 lakhs if it does. The quoted price (in lakhs of Rs.) of a vacant house is calculated as (base price) + 5 × (road adjacency value) + 3 × (neighbor count).It is also known that the maximum quoted price of a house in Block XX is Rs. 24 lakhs
It is given that some of the houses are occupied. The remaining ones are vacant and are the only ones available for sale.The base price of a vacant house is Rs. 10 lakhs if the house does not have a parking space, and Rs. 12 lakhs if it does. The quoted price (in lakhs of Rs.) of a vacant house is calculated as (base price) + 5 × (road adjacency value) + 3 × (neighbor count).It is also known that the maximum quoted price of a house in Block XX is Rs. 24 lakhs
Hence, there can be two cases for the maximum quoted price of a house in block XX.
Case 1: House with parking space:
=> 12+5a+3b = 24 => 5a+3b = 12 ( a = road adjacency value, b= neighbor count)
The only value for which the equation satisfies is (a = 0, and b=4). But the value of b can't be 4 because the maximum neighbor count can be at most 3.
Hence, case 1 is invalid.
Case 2: House without parking space:
=> 10+5a+3b = 24 => 5a+3b = 14
=> (a, b) = (1, 3)
Hence, the house must have 3 neighbors and 1 road connected to it. Hence, the only possible case is B2. Therefore, the neighbor houses of B2, which are (B1, A2, and C2) are occupied.
It is known that Row 1 has two occupied houses, one in each block. Since B1 is already occupied, it implies A1, and C1 are vacant.
Hence, the configuration of block XX is given below: (Where U = Unoccupied/ Vacant, and U = Occupied)
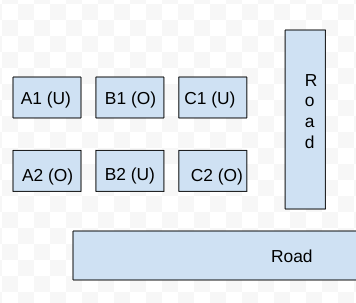 Now for block YY, we know that both houses in Column E are vacant. Each of Column-D and Column-F has at least one occupied house. There is only one house with parking space in Block YY.
Now for block YY, we know that both houses in Column E are vacant. Each of Column-D and Column-F has at least one occupied house. There is only one house with parking space in Block YY.
It is also known that the minimum quoted price of a house in block YY is Rs. 15 lakhs, and one such house is in Column E.
Case 1: The minimum quoted house is E2:
We know that the road adjacency of E2 is 1, hence we can calculate whether the house has parking space or not, and the neighbor count (b)
If the house has parking space, then: 12+5*1+3*b = 15 => 3b = -2 (which is not possible)
Hence, the house has no parking space => 10+5*1+3b = 15 => b = 0
b = 0 implies all the neighbor house of E2 is vacant, which are (E1, D2, and F2).
It is known that each of Column-D and Column-F has at least one occupied house, which implies D1, and F1 must be occupied.
But D1 and F1 can't be occupied together since the total number of occupied houses in Row 1 is 2 (one in each block).
Hence, This case is invalid.
Case 2: The minimum quoted house is E1:
We know that the road adjacency of E1 is 0, hence we can calculate whether the house has parking space or not, and the neighbor count (b).
i) If the house has no working space, then: 10+5*0+3b = 15 => b = 5/3 (this is not possible since b has to be an integer value)
Hence, the house has parking space => 12+5*0+3b = 15 => b = 1 => One neighbor house is occupied among D1 and F1.
Let's take the case of house D1 being occupied and F1 being empty. In that case, the value of house F1 would be 10(there is no parking space)+ (5*0) + (3*the number of neighbours)
Here, even if we take the number of neighbors to be 1, which is the maximum for F1 in this case, the value of F1 would be a maximum of 13. This is lower than the lowest-value house in block YY. Therefore, F1 cannot be empty.
Since F1 is occupied and we know that there is only one house occupied in row 1 of each block, D1 becomes unoccupied. D2 becomes occupied because it is given in the question that each of Column-D and Column-F has at least one occupied house.
Here, the value of D1 is 18 as D2 is occupied.
We do not know the status of house F2.
Therefore, the final diagram is given below:
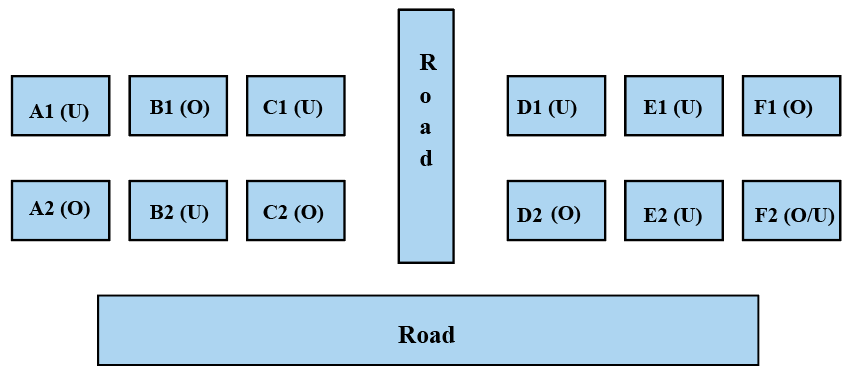 From the diagram, the vacant house with the maximum possible quoted price in column E is E2 when F2 is occupied.
From the diagram, the vacant house with the maximum possible quoted price in column E is E2 when F2 is occupied.
The maximum possible quoted price of E2 is 10+5*1+3*2 = 21 Lacs. ( E2 has no parking space because E1 has the parking space, and it is given that there is only one house with parking space in Block YY.)
Q4: Which house in Block YY has parking space?
 View Answer
View Answer 
Ans: E1
 It is given that some of the houses are occupied. The remaining ones are vacant and are the only ones available for sale.
It is given that some of the houses are occupied. The remaining ones are vacant and are the only ones available for sale.
The base price of a vacant house is Rs. 10 lakhs if the house does not have a parking space, and Rs. 12 lakhs if it does. The quoted price (in lakhs of Rs.) of a vacant house is calculated as (base price) + 5 × (road adjacency value) + 3 × (neighbor count).
It is also known that the maximum quoted price of a house in Block XX is Rs. 24 lakhs
Hence, there can be two cases for the maximum quoted price of a house in block XX.
Case 1: House with parking space:
=> 12+5a+3b = 24 => 5a+3b = 12 ( a = road adjacency value, b= neighbor count)
The only value for which the equation satisfies is (a = 0, and b=4). But the value of b can't be 4 because the maximum neighbor count can be at most 3.
Hence, case 1 is invalid.
Case 2: House without parking space:
=> 10+5a+3b = 24 => 5a+3b = 14
=> (a, b) = (1, 3)
Hence, the house must have 3 neighbors and 1 road connected to it. Hence, the only possible case is B2. Therefore, the neighbor houses of B2, which are (B1, A2, and C2) are occupied.
It is known that Row 1 has two occupied houses, one in each block. Since B1 is already occupied, it implies A1, and C1 are vacant.
Hence, the configuration of block XX is given below: (Where U = Unoccupied/ Vacant, and U = Occupied)
 Now for block YY, we know that both houses in Column E are vacant. Each of Column-D and Column-F has at least one occupied house. There is only one house with parking space in Block YY.
Now for block YY, we know that both houses in Column E are vacant. Each of Column-D and Column-F has at least one occupied house. There is only one house with parking space in Block YY.
It is also known that the minimum quoted price of a house in block YY is Rs. 15 lakhs, and one such house is in Column E.
Case 1: The minimum quoted house is E2:
We know that the road adjacency of E2 is 1, hence we can calculate whether the house has parking space or not, and the neighbor count (b)
If the house has parking space, then: 12+5*1+3*b = 15 => 3b = -2 (which is not possible)
Hence, the house has no parking space => 10+5*1+3b = 15 => b = 0
b = 0 implies all the neighbor house of E2 is vacant, which are (E1, D2, and F2).
It is known that each of Column-D and Column-F has at least one occupied house, which implies D1, and F1 must be occupied.
But D1 and F1 can't be occupied together since the total number of occupied houses in Row 1 is 2 (one in each block).
Hence, This case is invalid.
Case 2: The minimum quoted house is E1:
We know that the road adjacency of E1 is 0, hence we can calculate whether the house has parking space or not, and the neighbor count (b).
i) If the house has no working space, then: 10+5*0+3b = 15 => b = 5/3 (this is not possible since b has to be an integer value)
Hence, the house has parking space => 12+5*0+3b = 15 => b = 1 => One neighbor house is occupied among D1 and F1.
Let's take the case of house D1 being occupied and F1 being empty. In that case, the value of house F1 would be 10(there is no parking space)+ (5*0) + (3*the number of neighbours)
Here, even if we take the number of neighbors to be 1, which is the maximum for F1 in this case, the value of F1 would be a maximum of 13. This is lower than the lowest-value house in block YY. Therefore, F1 cannot be empty.
Since F1 is occupied and we know that there is only one house occupied in row 1 of each block, D1 becomes unoccupied. D2 becomes occupied because it is given in the question that each of Column-D and Column-F has at least one occupied house.
Here, the value of D1 is 18 as D2 is occupied.
We do not know the status of house F2.
Therefore, the final diagram is given below:
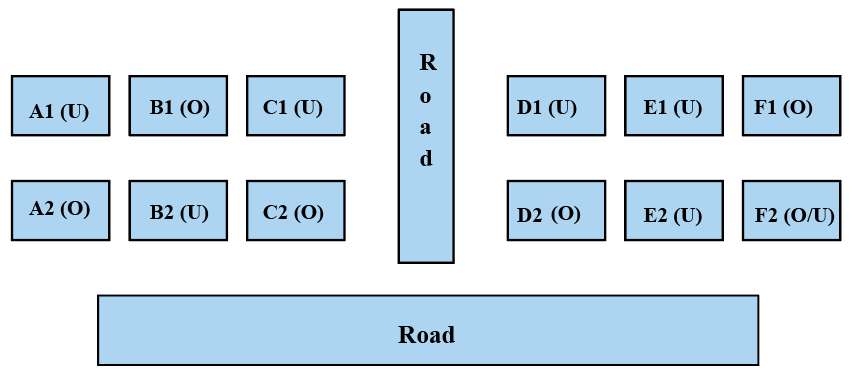 From the diagram, we can see that E1 has the parking space (case 2).
From the diagram, we can see that E1 has the parking space (case 2).
The correct option is A
Que 3: Instruction for Set 3 (2021)
Twenty five coloured beads are to be arranged in a grid comprising of five rows and five columns. Each cell in the grid must contain exactly one bead. Each bead is coloured either Red, Blue or Green. While arranging the beads along any of the five rows or along any of the five columns, the rules given below are to be followed:
1. Two adjacent beads along the same row or column are always of different colours.
2. There is at least one Green bead between any two Blue beads along the same row or column.
3. There is at least one Blue and at least one Green bead between any two Red beads along the same row or column.
Every unique, complete arrangement of twenty five beads is called a configuration.
Q1: The total number of possible configurations using beads of only two colours is:
 View Answer
View Answer 
Ans: 2
Since we are required to use only two colours, these can be either
1. Green + Blue
2. Blue + Red
3. Green + Red
But we know that Between any two Red coloured beads in a row or a column, there have to be both a Green and a Blue coloured bead. Hence without both Green and Blue, Red beads cannot be used to fill the grid.Thus if we use only Green and Blue beads, the two configurations that are possible are:
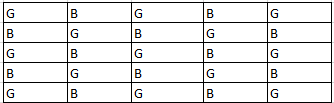 There are only 2 configurations possible
There are only 2 configurations possible
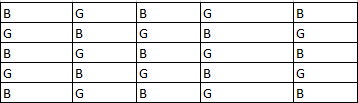
Q2: What is the maximum possible number of Red beads that can appear in any configuration?
 View Answer
View Answer 
Ans: 9
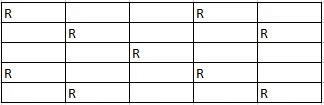 Maximum 9 red beads are possible as shown here
Maximum 9 red beads are possible as shown hereQ3: What is the minimum number of Blue beads in any configuration?
 View Answer
View Answer 
Ans: 6
To solve this question we can use the answer of the previous question, since maximum 9 red beads are possible, filling the remaining space with green and blue beads, in such a way that number of blue beads is minimised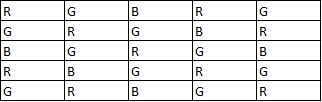
Hence number of blue beads is 6
Q4: Two Red beads have been placed in ‘second row, third column’ and ‘third row, second column’. How many more Red beads can be placed so as to maximise the number of Red beads used in the configuration?
 View Answer
View Answer 
Ans: 6
6 more beads can be placed as shown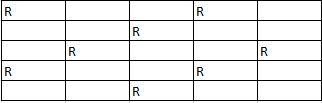
|
77 videos|180 docs|96 tests
|
FAQs on TITA Based Questions : Arrangements and Puzzles - Logical Reasoning (LR) and Data Interpretation (DI) - CAT
| 1. What are TITA questions in the UPSC exam? |  |
| 2. How are arrangements and puzzles important in UPSC preparation? |  |
| 3. What strategies can be adopted for solving arrangement and puzzle questions in UPSC? |  |
| 4. Are there any specific books or resources recommended for TITA based questions in UPSC? |  |
| 5. How can candidates improve their performance in TITA questions specifically related to arrangements and puzzles? |  |
















