TITA Based Questions: Set theory | Logical Reasoning (LR) and Data Interpretation (DI) - CAT PDF Download
As TITA (Type In The Answer) based questions are gaining prominence in the CAT exam, it’s important to build accuracy without relying on options. The following are carefully curated TITA-based questions on the topic Set Thoery to help you practice exact value-based problem solving.

Q1: Set P comprises all multiples of 4 less than 500. Set Q comprises all odd multiples of 7 less than 500, Set R comprises all multiples of 6 less than 500. How many elements are present in {P ∪ Q ∪ R}?
 View Answer
View Answer 
Ans: 202
This question involves both Number Systems and Set Theory.
Set P = {4, 8, 12, ….496} ↦ 124 elements {all elements from 1 * 4 to 124 * 4}
Set Q = {7, 21, 35, 49,……497} ↦ {7 * 1, 7 * 3, 7 * 5, ….. 7 * 71} ↦ 36 elements.
Set R = {6, 12, 18, 24, …..498} ↦ {6 * 1, 6 * 2, 6 * 3, ….. 6 * 83} ↦ 83 elements.
Sets P and R have only even numbers; set Q has only odd numbers. So,
P ∩ Q = Null set
Q ∩ R = Null set
P ∩ Q ∩ R = Null set
So, If we find P ∩ R , we can plug into the formula and get P ∪ Q ∪ R
P ∩ R = Set of all multiples of 12 less than 500 = {12, 24, 36,…..492}
= {12 * 1, 12 * 2 , 12 * 3, …12 * 41} ↦ This has 41 elements
P ∪ Q ∪ R = P + Q + R – (P ∩ Q) – ( Q ∩ R) – (R ∩ P) + (P ∩ Q ∩ R)
P ∪ Q ∪ R = 124 + 36 + 83 – 0 – 0 – 41 + 0 = 202
Q2: Set A comprises all three digit numbers that are multiples of 5, Set B comprises all three–digit even numbers that are multiples of 3 and Set C comprises all three–digit numbers that are multiples of 4. How many elements are present in A ∪ B ∪ C?
 View Answer
View Answer 
Ans: 420
Set A = {100, 105, 110, ….995} ↦ {5 * 20, 5 * 21, ….. 5 * 199} ↦ 180 elements.
Set B = {102, 108, 114, ……996} ↦ {6 * 17, 6 * 18, 6 * 19, ….. 6 * 166} ↦ 150 elements.
Set C = {100, 104, 108, …..996} ↦ {4 * 25, 4 * 26, ….. 4 * 249} ↦ 225 elements.
A ∩ B = {120, 150, 180, …..990} ↦ All 3-digit multiples of 30 ↦ 30 elements.
B ∩ C = {108, 120, 132, …..996} ↦ All 3-digit multiples of 12 ↦ 75 elements.
C ∩ A = {120, 140, 160, …..980} ↦ All 3-digit multiples of 20 ↦ 45 elements.
A ∩ B ∩ C = {120, 180, …..960} ↦ All 3-digit multiples of 60 ↦ 15 elements.
A ∪ B ∪ C = A + B + C – A ∩ B – B ∩ C – C ∩ A + A ∩ B ∩ C
= 180 + 150 + 225 – 30 – 75 – 45 + 15 = 420
Q3: Sonu started a new business with accounts in two different banks (i.e. Axis and SBI).He deposited the earnings of each day in either of the two banks. However he does not deposit his earnings in both the banks simultaneously on any given day. However somehow he could not carry the business for long and had to shut it down. Find the total no of days Sonu carried on the business if…
(1) He did not deposited in axis bank on 20 days and in SBI on 24 days.
(2) He deposited on either axis bank or SBI on 28 days.
 View Answer
View Answer 
Ans: 36
Let the total No. of days Sonu deposited the earnings in Axis bank be ‘n(a)’ and
that in SBI be ‘n(b)’
Now,
Total no of days he carried on the business = n(a) + n(b) – n(a∩b) + Neither (Days he didn’t earned)
Since on any given day he does not deposit in both the bank accounts
n(a∩b) = 0
Hence,
Total no of days he carried on the business = n(a) + n(b) + Neither (Days he didn’t earned)
Now,
A/Q
Total – n(a) = 20……………………………(1)
Total – n(b) = 24……………………………(2)
n(a) + n(b) = 28………………………………(3)
Solving the 3 equations we get,
n(a) = 16
n(b) = 12
Q4: A class in college has 150 students numbered from 1 to 150 , in which all the even numbered students are doing CA, whose number are divisible by 5 are doing Actuarial and those whose numbers are divisible by 7 are preparing for MBA. How many of the students are doing nothing?
 View Answer
View Answer 
Ans: 51
Let the total no of students doing CA be n(A), those doing actuarial be n(B) and those doing MBA be n(C).
Now, ‘CA’ is a set of all even numbered students, thus 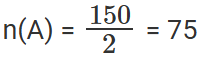
‘Actuarial’ is a set of all the students whose number are divisible by 5, thus n(B) = 150/5 = 30
‘MBA’ is a set of all the students whose number are divisible by 7, thus n(C) = 150/7 = 21
The 10th, 20th, 30th…… numbered students would be doing both CA and Actuarial
∴ n(A∩B) = 150/10 = 5
The 14th, 28th, 42nd…… numbered students would be doing both CA and MBA
∴ n(A∩C) = 150/40 = 10
The 35th, 70th, …… numbered students would be doing both Actuarial and MBA
∴ n(B∩C) = 150/35 = 4
And the 70th and 140th students must be doing all the three.
∴n(A∩B∩C) = 2
Now, n(A∪B∪C) = n(A)+n(B)+n(C) – n(A∩B) – n(A∩C) - n(B∩C) + n(A∩B∩C) = 99
∴ Number of students doing nothing = 150 – 99 = 51
Q5: In a class of 345 students, the students who took English, Math and Science are equal in number. There are 30 students who took both English and Math, 26 who took both Math and Science, 28 who took Science and English and 14 who took all the 3 subjects.There are 43 students who didn’t take any of the subjects. Answer the following question according to the data given above.
How many students have taken English as a subject?
 View Answer
View Answer 
Ans: 124
Let total no of students who took English be x
Then students who took math, science will also be x
Now let’s draw the Venn diagram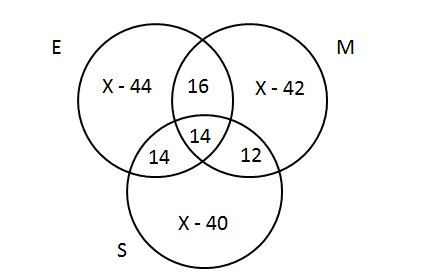 E U M U S = 345 – 43 (Neither of the subjects)
E U M U S = 345 – 43 (Neither of the subjects)
E U M U S = E + M + S – E ∩ M - E ∩ S - S ∩ M + E ∩ M ∩ S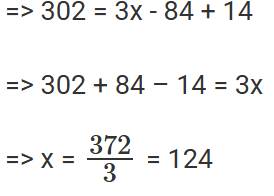 Thus the total no of students who took English as a subject = 124
Thus the total no of students who took English as a subject = 124
Consequently the Venn diagram becomes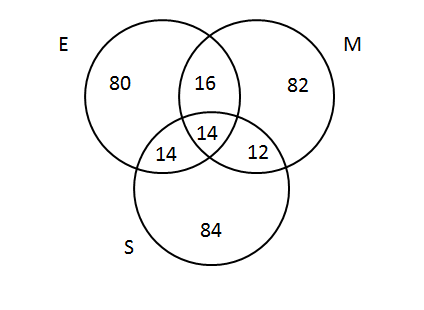
Again,
The students who has taken only one subject = E U M U S - E ∩ M - E ∩ S - S ∩ M - E ∩ M ∩ S
= 302 - 16 - 14 - 14 - 12 = 246
The students who took English and Math but not science = only E + Only M + E ∩ M
= 80 + 82 + 16 = 178
Percent of students who took English and Math but not science = 178/302 * 100 = approx. 59 %
Hence, the answer is "124".
Q6: In a survey conducted to know people’s preference for android phones and I phones, 80 person preferred android phones while 60 person preferred I phones. There were 20 who liked both and may prefer any. If there was no one who didn’t prefer at least one of the phones,then on how many people was the survey conducted?
 View Answer
View Answer 
Ans: 120
Diagrammatic Approach -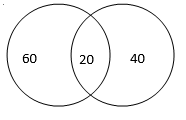
It is quite clear from the diagram that the number of people at the party were 60 + 20 + 40 = 120Mathematical approach :
Let n(A) be the no. of persons that prefers android phones , the no of persons that prefers IOS be n(B) and n(A∩B) be the persons who liked both may prefer both.Thus using the formula n(AUB) = n(A) + n(B) – n(A∩B)
n(AUB) = 80 + 60 – 20 = 120
Q7: In Grand Oberoi hotel, 1160 guests are present currently. The hotel provides the following extra facilities: Gym, Swimming, Fun park, Food. During a regular survey the management team of Oberoi noticed something quite extraordinary about the extra facilities provided by them. They noticed that for every person who uses ‘F’ no. of facilities, there are exactly 3 persons who uses at least (F-1) no. of facilities, F = 2, 3, 4. They also found that the no. of persons who used no extra facilities is twice the no of person that used all the 4 facilities. Help the management team to find out how many persons used exactly 3 facilities.
 View Answer
View Answer 
Ans: 80
Since, for every person who uses ‘F’ no of facilities, there are exactly 3 person who uses atleast (F-1) no. of facilities. If we take the no. of persons who uses all the four facilities to be ‘x’ then the no. of person who uses atleast 3 facilities will be 3x and so on.
The No. of persons who use exactly 3 facilities = 3x – x = 2x
Thus, the no. of persons who opt for various facilities can be summarized as follows:
| n | number of person who uses atleast n facilities | number of person who uses exactly in facilities |
|---|---|---|
| 4 | x | x |
| 3 | 3x | 2x |
| 2 | 9x | 6x |
| 1 | 27x | 18x |
We also know that no of person who uses no facilities = twice of those who uses all the 4 facilities = 2x.
So according the above deductions we can clearly see that the number of person the hotel would be
x + 2x + 6x + 18x + 2x = 29 x = 1160
x = 40
Hence the number of person who uses exactly three science = 2x = 80
Q8: In its annual fest, a college is organizing three events: B-quiz, Finance and Marketing. The college has a strength of 510 students.The students were allowed to participate in any no. of events they liked. While viewing the statistics of the performance, the general secretary noticed:-
1. The number of students who participated in atleast two events were 52% more than those who participated in exactly one game.
2. The no. of students participating in 1,2 or 3 events respectively was atleast equal to 1.
3. The number of students who did not participate in any of the three events was the minimum possible integral value under these conditions.
What can be the maximum no. of students who participated in exactly 3 games?
 View Answer
View Answer 
Ans: 303
Let the no. of students who participated in 0,1,2,3 games be A, B, C, D respectively.
Then from the information we have we can conclude that
C + D = 152% 0f B = 1.52 of B -----------------------(1)
Since the total no. of students the college has is 420,
A + B + C + D = 510 ---------------------------------(2)
From (1) and (2), we can conclude that
A + 2.52B = 510
B = 25/635* (510 – A)
For A to be minimum, 510 – A should give us the largest multiple of 63. Since, 63 * 8 = 504 we will get A = 6.
So B = 200 and C + D = 1.52 B = 304
Thus for the students participating in exactly 3 games to be maximum, the number of students participating in exactly 2 games has to be minimized and made equal to 1.
Thus no of students who participated in exactly 3 games = 304 – 1 = 303.
Q9: A factory has 80 workers and 3 machines. Each worker knows to operate atleast 1 machine. If there are 65 persons who knows to operate machine 1, 60 who knows to operate machine 2 and 55 who knows to operate machine 3, what can be the minimum number of persons who knows to operate all the three machines?
 View Answer
View Answer 
Ans: 20
Let’s start with taking a random value for all three category. So let’s first take 40 for the all three category. Now 65 + 60 + 55 = 180, this means there is an extra count of 180 – 80 = 100.
Now as we know that the extra count occurs in the in the exactly two area and the all three area. So let’s try put the extra count in these area.
Trial 1 - Since 40 is already assumed to be in the all three area, it takes care of extra count of 40 x 2 = 80. Thus we are left with 20 as extra count which we have to place at the exactly two area
Thus in the above case our venn diagram will look as: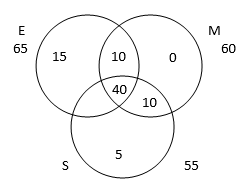
A close look in the figure tells us that we can further decrease the value of all the three area. A bit of logical thinking will bring us to the value 20. No value less than 20 can satisfy the conditions of the question. As there is no scope left for reallocating numbers left from one area to another in this case.
Hence the final venn diagram will look as: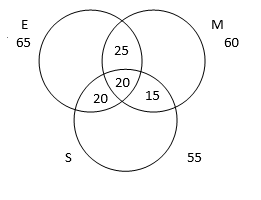
|
77 videos|180 docs|96 tests
|
FAQs on TITA Based Questions: Set theory - Logical Reasoning (LR) and Data Interpretation (DI) - CAT
| 1. Che cos'è l'insieme in teoria degli insiemi? |  |
| 2. Qual è la differenza tra un insieme e un sottoinsieme? |  |
| 3. Come si rappresentano gli insiemi? |  |
| 4. Cosa sono le operazioni sugli insiemi? |  |
| 5. Qual è l'importanza della teoria degli insiemi nella matematica? |  |





















