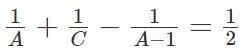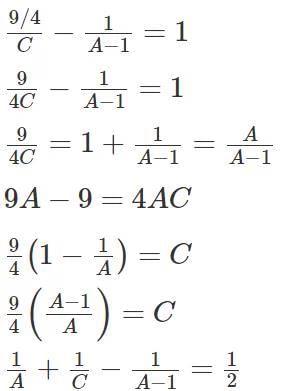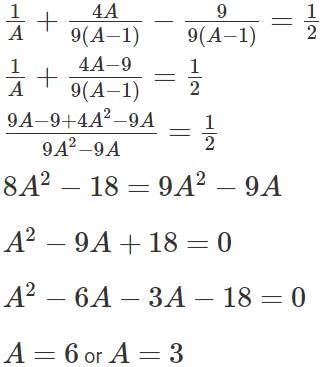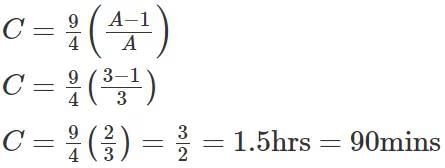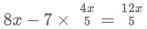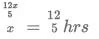CAT Exam > CAT Notes > Quantitative Aptitude (Quant) > CAT Previous Year Questions - Pipes and Cisterns
CAT Previous Year Questions - Pipes and Cisterns | Quantitative Aptitude (Quant) PDF Download
2023
Q1: Pipes A and C are fill pipes while Pipe B is a drain pipe of a tank. Pipe B empties the full tank in one hour less than the time taken by Pipe A to fill the empty tank. When pipes A, B and C are turned on together, the empty tank is filled in two hours. If pipes B and C are turned on together when the tank is empty and Pipe B is turned off after one hour, then Pipe C takes another one hour and 15 minutes to fill the remaining tank. If Pipe A can fill the empty tank in less than five hours, then the time taken, in minutes, by Pipe C to fill the empty tank is
(a) 90
(b) 60
(c) 120
(d) 75
Ans: a
Sol: Let A, B and C be the number of hours taken by pipes A, B and C to completely fill (or completely empty) a tank.
So the fraction of the tank filled(or emptied) by them in one hour is 1/A, 1/B, 1/C
“Pipe B empties the full tank in one hour less than the time taken by Pipe A to fill the empty tank”
B = A – 1
“When pipes A, B and C are turned on together, the empty tank is filled in two hours”If pipes B and C are turned on together when the tank is empty and Pipe B is turned off after one hour, then Pipe C takes another one hour and 15 minutes to fill the remaining tank.”
This means, after pipe C worked for 2 hrs 15 mins (or 9/4 hrs) and the Pipe B draining for 1 hour, the tank got filled.“Pipe A can fill the empty tank in less than five hours” A = 3
2021
Q1: Two pipes A and B are attached to an empty water tank. Pipe A fills the tank while pipe B drains it. If pipe A is opened at 2 pm and pipe B is opened at 3 pm, then the tank becomes full at 10 pm. Instead, if pipe A is opened at 2 pm and pipe B is opened at 4 pm, then the tank becomes full at 6 pm. If pipe B is not opened at all, then the time, in minutes, taken to fill the tank is
(a) 144
(b) 140
(c) 264
(d) 120
Ans: (a)
Sol: Let A fill the tank at x liters/hour and B drain it at y liters/hour
Now as per Condition 1 :
We get Volume filled till 10pm = 8x-7y (1) .
Here A operates for 8 hours and B operates for 7 hours .
As per condition 2
We get Volume filled till 6pm = 4x-2y (2)
Here A operates for 4 hours and B operates for 2 hours .
Now equating (1) and (2)
we get 8x-7y =4x-2y
so we get 4x =5y
y =4x/5
So volume of tank =So time taken by A alone to fill the tank =
= 144 minutes
The document CAT Previous Year Questions - Pipes and Cisterns | Quantitative Aptitude (Quant) is a part of the CAT Course Quantitative Aptitude (Quant).
All you need of CAT at this link: CAT
|
166 videos|231 docs|95 tests
|
FAQs on CAT Previous Year Questions - Pipes and Cisterns - Quantitative Aptitude (Quant)
| 1. What are pipes and cisterns in the context of quantitative aptitude? |  |
Ans. Pipes and cisterns refer to a common topic in quantitative aptitude that deals with problems involving fluid flow. In these problems, pipes are used to fill or drain a tank (cistern), and the focus is on calculating the time taken to fill or empty the tank based on the rates of the pipes involved.
| 2. How do you calculate the time taken to fill a tank using multiple pipes? | |
Ans. To calculate the time taken to fill a tank using multiple pipes, you need to determine the rate at which each pipe fills the tank. You can add the rates of the pipes together to get a combined rate. The time taken to fill the tank can then be calculated by dividing the volume of the tank by the combined rate.
| 3. What is the formula for solving problems related to pipes and cisterns? | |
Ans. The general formula to solve problems involving pipes and cisterns is: Time = Volume / Rate. For a single pipe, the rate is usually given in terms of the tank's volume per hour. For multiple pipes, you sum their rates and then apply the formula accordingly.
| 4. Can pipes also drain a tank, and how does this affect calculations? | |
Ans. Yes, pipes can drain a tank, and this will affect calculations by reducing the effective rate of filling the tank. When a draining pipe is involved, its rate is subtracted from the rate of filling pipes to find the net rate at which the tank is filled or emptied.
| 5. What are some common pitfalls to avoid when solving pipes and cisterns problems? | |
Ans. Common pitfalls include neglecting to convert all rates to the same unit, not accounting for the time taken by draining pipes, mistakenly adding instead of subtracting rates, and forgetting to check if the problem asks for the time to fill or drain the tank. Always read the problem carefully to understand what is being asked.
About this Document
Sep 26, 2025
Last updated
Document Description: CAT Previous Year Questions - Pipes and Cisterns for CAT 2025 is part of Quantitative Aptitude (Quant) preparation.
The notes and questions for CAT Previous Year Questions - Pipes and Cisterns have been prepared according to the CAT exam syllabus. Information about CAT Previous Year Questions - Pipes and Cisterns covers topics
like 2023, 2021 and CAT Previous Year Questions - Pipes and Cisterns Example, for CAT 2025 Exam. Find important definitions, questions, notes, meanings, examples, exercises and tests below for CAT Previous Year Questions - Pipes and Cisterns.
Introduction of CAT Previous Year Questions - Pipes and Cisterns in English is available as part of our Quantitative Aptitude (Quant)
for CAT & CAT Previous Year Questions - Pipes and Cisterns in Hindi for Quantitative Aptitude (Quant) course.
Download more important topics related with notes, lectures and mock test series for CAT
Exam by signing up for free. CAT: CAT Previous Year Questions - Pipes and Cisterns | Quantitative Aptitude (Quant)
Description
Full syllabus notes, lecture & questions for CAT Previous Year Questions - Pipes and Cisterns | Quantitative Aptitude (Quant) - CAT | Plus excerises question with solution to help you revise complete syllabus for Quantitative Aptitude (Quant) | Best notes, free PDF download
Information about CAT Previous Year Questions - Pipes and Cisterns
In this doc you can find the meaning of CAT Previous Year Questions - Pipes and Cisterns defined & explained in the simplest way possible. Besides explaining types of
CAT Previous Year Questions - Pipes and Cisterns theory, EduRev gives you an ample number of questions to practice CAT Previous Year Questions - Pipes and Cisterns tests, examples and also practice CAT
tests
Related Searches
ppt
,Exam
,Free
,MCQs
,Previous Year Questions with Solutions
,Summary
,shortcuts and tricks
,Objective type Questions
,CAT Previous Year Questions - Pipes and Cisterns | Quantitative Aptitude (Quant)
,Sample Paper
,study material
,past year papers
,CAT Previous Year Questions - Pipes and Cisterns | Quantitative Aptitude (Quant)
,video lectures
,Important questions
,mock tests for examination
,practice quizzes
,Viva Questions
,CAT Previous Year Questions - Pipes and Cisterns | Quantitative Aptitude (Quant)
,Semester Notes
,Extra Questions
;
Additional Information about CAT Previous Year Questions - Pipes and Cisterns for CAT Preparation
CAT Previous Year Questions - Pipes and Cisterns Free PDF Download
The CAT Previous Year Questions - Pipes and Cisterns is an invaluable resource that delves deep into the core of the CAT exam.
These study notes are curated by experts and cover all the essential topics and concepts, making your preparation more efficient and effective.
With the help of these notes, you can grasp complex subjects quickly, revise important points easily,
and reinforce your understanding of key concepts. The study notes are presented in a concise and easy-to-understand manner,
allowing you to optimize your learning process. Whether you're looking for best-recommended books, sample papers, study material,
or toppers' notes, this PDF has got you covered. Download the CAT Previous Year Questions - Pipes and Cisterns now and kickstart your journey towards success in the CAT exam.
Importance of CAT Previous Year Questions - Pipes and Cisterns
The importance of CAT Previous Year Questions - Pipes and Cisterns cannot be overstated, especially for CAT aspirants.
This document holds the key to success in the CAT exam.
It offers a detailed understanding of the concept, providing invaluable insights into the topic.
By knowing the concepts well in advance, students can plan their preparation effectively.
Utilize this indispensable guide for a well-rounded preparation and achieve your desired results.
CAT Previous Year Questions - Pipes and Cisterns Notes
CAT Previous Year Questions - Pipes and Cisterns Notes offer in-depth insights into the specific topic to help you master it with ease.
This comprehensive document covers all aspects related to CAT Previous Year Questions - Pipes and Cisterns.
It includes detailed information about the exam syllabus, recommended books, and study materials for a well-rounded preparation.
Practice papers and question papers enable you to assess your progress effectively.
Additionally, the paper analysis provides valuable tips for tackling the exam strategically.
Access to Toppers' notes gives you an edge in understanding complex concepts.
Whether you're a beginner or aiming for advanced proficiency, CAT Previous Year Questions - Pipes and Cisterns Notes on EduRev are your ultimate resource for success.
CAT Previous Year Questions - Pipes and Cisterns CAT
The "CAT Previous Year Questions - Pipes and Cisterns CAT Questions" guide is a valuable resource for all aspiring students preparing for the
CAT exam. It focuses on providing a wide range of practice questions to help students gauge
their understanding of the exam topics. These questions cover the entire syllabus, ensuring comprehensive preparation.
The guide includes previous years' question papers for students to familiarize themselves with the exam's format and difficulty level.
Additionally, it offers subject-specific question banks, allowing students to focus on weak areas and improve their performance.
Study CAT Previous Year Questions - Pipes and Cisterns on the App
Students of CAT can study CAT Previous Year Questions - Pipes and Cisterns alongwith tests & analysis from the EduRev app,
which will help them while preparing for their exam. Apart from the CAT Previous Year Questions - Pipes and Cisterns,
students can also utilize the EduRev App for other study materials such as previous year question papers, syllabus, important questions, etc.
The EduRev App will make your learning easier as you can access it from anywhere you want.
The content of CAT Previous Year Questions - Pipes and Cisterns is prepared as per the latest CAT syllabus.
|
© EduRev
|
Education Revolution
|
|
Signup to see your scores
go up within 7 days!
Access 1000+ FREE Docs, Videos and Tests
Takes less than 10 seconds to signup