CAT Previous Year Questions - Team Formations | Logical Reasoning (LR) and Data Interpretation (DI) PDF Download
In 2023, the CAT exam included questions on team formations, focusing on departmental voting patterns and strategic box configurations. These questions test logical deduction, distribution analysis, and optimisation within structured systems, with scenarios involving faculty voting and sack arrangements in a grid.
2023
Passage - 1
Instructions
Faculty members in a management school can belong to one of four departments - Finance and Accounting (F&A), Marketing and Strategy (M&S), Operations and Quants (O&Q) and Behaviour and Human Resources (B&H). The numbers of faculty members in F&A, M&S, O&Q and B&H departments are 9, 7, 5 and 3 respectively.
Prof. Pakrasi, Prof. Qureshi, Prof. Ramaswamy and Prof. Samuel are four members of the school's faculty who were candidates for the post of the Dean of the school. Only one of the candidates was from O&Q.
Every faculty member, including the four candidates, voted for the post. In each department, all the faculty members who were not candidates voted for the same candidate. The rules for the election are listed below.
1. There cannot be more than two candidates from a single department.
2. A candidate cannot vote for himself/herself.
3. Faculty members cannot vote for a candidate from their own department.
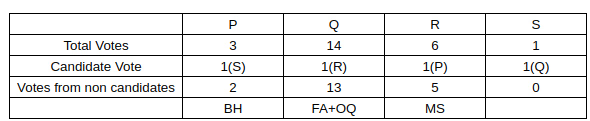
After the election, it was observed that Prof. Pakrasi received 3 votes, Prof. Qureshi received 14 votes, Prof. Ramaswamy received 6 votes and Prof. Samuel received 1 vote. Prof. Pakrasi voted for Prof. Ramaswamy, Prof. Qureshi for Prof. Samuel, Prof. Ramaswamy for Prof. Qureshi and Prof. Samuel for Prof. Pakrasi.
Q1: Which two candidates can belong to the same department?
(a) Prof. Pakrasi and Prof. Qureshi
(b) Prof. Pakrasi and Prof. Samuel
(c) Prof. Qureshi and Prof. Ramaswamy
(d) Prof. Ramaswamy and Prof. Samuel
Ans: a
Sol: Now, we know there is only 1 candidate from OQ, which means that the number of non-candidate voters in OQ will be 4.
We also know that the non-candidates in a particular department voted as a block, and we also know that the least number of non-candidate voters in a particular department can be 1 (BH, 3-2 faculty).
Now, we also know that R got 5 votes from non-candidates.
Now we can write 5 as
(i) 5
(ii) 4+1
(iii) 3+2
Considering case (i) 4+1. This is only possible when there is 1 candidate from OQ, and there are 2 candidates from BH. This implies that the number of candidates in FA and MQ is 1. Now, if we consider FA and MQ and put only 1 candidate there, it implies that there are 15 non-candidate voters between them. Now we know this is not possible since the maximum number of non-candidate voters a candidate can get is 13. (Please note that non-candidates of a particular department vote as a block).
On similar grounds, we can eliminate Case (iii) as it also implies there is only 1 candidate in FA and MQ.
Now, considering Case (i), we know that 5+0 will happen only one when there are 5 non-candidates in a single department. This is only possible in MS (Out of 7, there will be 2 candidates and 5 non-candidates).
So we can conclude that MS has 2 candidates and that they voted Prof. R…….(i)
We also know that Prof P got 2 votes from Non-candidates. This is only possible when BH has 1 candidate.
So, we can conclude that the number of professors in FA, MS, OQ, BH is 0,2,1,1
Thus, we get the following table:
Now, if we consider Department MS, we know that there are 2 candidates from MS and R can’t be one of them as the people in that department voted for him….. (3 rd condition).
So the possible combinations of candidates in MS are (P,Q), (Q,S), (P,S).
Now we also know that no one can vote for a candidate in their own department, so we can eliminate (P,S) and (Q,S) as we know that S voted for P and Q voted for S).
So we can infer that P and Q are from MS.
Now, among the given options, Only Option A is true. Therefore, Option A is the correct answer.
Q2: Which of the following can be the number of votes that Prof. Qureshi received from a single department?
(a) 7
(b) 6
(c) 8
(d) 9
Ans: d
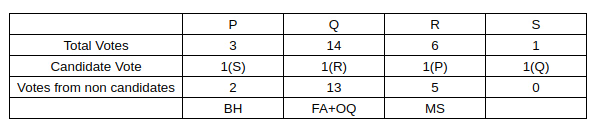
Sol: Now, we know there is only 1 candidate from OQ, which means that the number of non-candidate voters in OQ will be 4.
We also know that the non-candidates in a particular department voted as a block, and we also know that the least number of non-candidate voters in a particular department can be 1 (BH, 3-2 faculty).
Now, we also know that R got 5 votes from non-candidates.
Now we can write 5 as
(i) 5
(ii) 4+1
(iii) 3+2
Considering case (i) 4+1. This is only possible when there is 1 candidate from OQ, and there are 2 candidates from BH. This implies that the number of candidates in FA and MQ is 1. Now, if we consider FA and MQ and put only 1 candidate there, it implies that there are 15 non-candidate voters between them. Now, we know this is not possible since the maximum number of non-candidate voters a candidate can get is 13. (Please note that non-candidates of a particular department vote as a block).
On similar grounds, we can eliminate Case (iii) as it also implies there is only 1 candidate in FA and MQ.
Now, considering Case (i), we know that 5+0 will happen only once when there are 5 non-candidates in a single department. This is only possible in MS (Out of 7, there will be 2 candidates and 5 non-candidates).
So we can conclude that MS has 2 candidates and that they voted Prof. R…….(i)
We also know that Prof P got 2 votes from Non-candidates. This is only possible when BH has 1 candidate.
So, we can conclude that the number of professors in FA, MS, OQ, BH is 0,2,1,1
Thus, we get the following table:
Now, if we consider Department MS, we know that there are 2 candidates from MS and R can’t be one of them as the people in that department voted for him….. (3 rd condition).
So, the possible combinations of candidates in MS are (P,Q), (Q,S), (P,S).
Now we also know that no one can vote for a candidate in their own department, so we can eliminate (P,S) and (Q,S) as we know that S voted for P and Q voted for S).
So, we can infer that P and Q are from MS.
Now, we can see that the number of votes that Prof Qureshi received from a single department can be 9 or 5 (if R is from OQ) or 4 (if R is not from OQ).
So, among the options, only Option D can be true. Therefore, Option D is the correct answer.
Q3: If Prof. Samuel belongs to B&H, which of the following statements is/are true?
Statement A: Prof. Pakrasi belongs to M&S.
Statement B: Prof. Ramaswamy belongs to O&Q
(a) Neither statement A nor statement B
(b) Only statement B
(c) Only statement A
(d) Both statements A and B
Ans: d
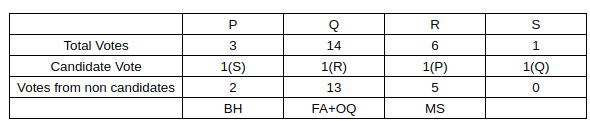
Sol: Now, we know there is only 1 candidate from OQ, which means that the number of non-candidate voters in OQ will be 4.
We also know that the non-candidates in a particular department voted as a block, and we also know that the least number of non-candidate voters in a particular department can be 1 (BH, 3-2 faculty).
Now, we also know that R got 5 votes from non-candidates.
Now we can write 5 as
(i) 5
(ii) 4+1
(iii) 3+2
Considering case (i) 4+1. This is only possible when there is 1 candidate from OQ, and there are 2 candidates from BH. This implies that the number of candidates in FA and MQ is 1. Now, if we consider FA and MQ and put only 1 candidate there, it implies that there are 15 non-candidate voters between them. Now we know this is not possible since the maximum number of non-candidate voters a candidate can get is 13. (Please note that non-candidates of a particular department vote as a block).
On similar grounds, we can eliminate Case (iii) as it also implies there is only 1 candidate in FA and MQ.
Now, considering Case (i), we know that 5+0 will happen only one when there are 5 non-candidates in a single department. This is only possible in MS (Out of 7, there will be 2 candidates and 5 non-candidates).
So we can conclude that MS has 2 candidates and that they voted Prof. R…….(i)
We also know that Prof P got 2 votes from Non-candidates. This is only possible when BH has 1 candidate.
So, we can conclude that the number of professors in FA, MS, OQ, BH is 0,2,1,1
Thus, we get the following table:
Now, if we consider Department MS, we know that there are 2 candidates from MS and R can’t be one of them as the people in that department voted for him….. (3 rd condition).
So the possible combinations of candidates in MS are (P,Q), (Q,S), (P,S).
Now we also know that no one can vote for a candidate in their own department, so we can eliminate (P,S) and (Q,S) as we know that S voted for P and Q voted for S).
So we can infer that P and Q are from MS.
We have been told Prof Samuel belongs to B&H. So we have to consider only Case 1. In Case 1 we can see that Prof Prakash belongs to MS and Prof Ramaswamy belongs to OQ.
Therefore, both the statements are true.
So, the correct answer is Option D
Q4: What best can be concluded about the candidate from O&Q?
(a) It was Prof. Samuel.
(b) It was either Prof. Ramaswamy or Prof. Samuel.
(c) It was Prof. Ramaswamy.
(d) It was either Prof. Pakrasi or Prof. Qureshi.
Ans: b
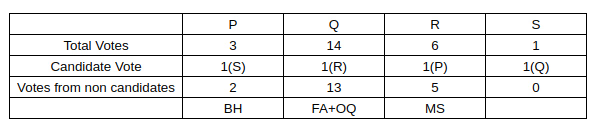
Sol: Now, we know there is only 1 candidate from OQ, which means that the number of non-candidate voters in OQ will be 4.
We also know that the non-candidates in a particular department voted as a block, and we also know that the least number of non-candidate voters in a particular department can be 1 (BH, 3-2 faculty).
Now, we also know that R got 5 votes from non-candidates.
Now we can write 5 as
(i) 5
(ii) 4+1
(iii) 3+2
Considering case (i) 4+1. This is only possible when there is 1 candidate from OQ, and there are 2 candidates from BH. This implies that the number of candidates in FA and MQ is 1. Now, if we consider FA and MQ and put only 1 candidate there, it implies that there are 15 non-candidate voters between them. Now we know this is not possible since the maximum number of non-candidate voters a candidate can get is 13. (Please note that non-candidates of a particular department vote as a block).
On similar grounds, we can eliminate Case (iii) as it also implies there is only 1 candidate in FA and MQ.
Now, considering Case (i), we know that 5+0 will happen only one when there are 5 non-candidates in a single department. This is only possible in MS (Out of 7, there will be 2 candidates and 5 non-candidates).
So we can conclude that MS has 2 candidates and that they voted Prof. R…….(i)
We also know that Prof P got 2 votes from Non-candidates. This is only possible when BH has 1 candidate.
So, we can conclude that the number of professors in FA, MS, OQ, BH is 0,2,1,1
Thus, we get the following table:
Now, if we consider Department MS, we know that there are 2 candidates from MS and R can’t be one of them as the people in that department voted for him….. (3 rd condition).
So the possible combinations of candidates in MS are (P,Q), (Q,S), (P,S).
Now we also know that no one can vote for a candidate in their own department, so we can eliminate (P,S) and (Q,S) as we know that S voted for P and Q voted for S).
So we can infer that P and Q are from MS.
From the 2 cases, we can see that the candidate from OQ can either be Prof Ramaswamy or Prof Samuel.
Therefore, the correct answer is Option B.
Q5: Which of the following statements is/are true?
Statement A: Non-candidates from M&S voted for Prof. Qureshi.
Statement B: Non-candidates from F&A voted for Prof. Qureshi.
(a) Both statements A and B
(b) Only statement B
(c) Only statement A
(d) Neither statement A nor statement B
Ans: b
Sol: Now, we know there is only 1 candidate from OQ, which means that the number of non-candidate voters in OQ will be 4.
We also know that the non-candidates in a particular department voted as a block, and we also know that the least number of non-candidate voters in a particular department can be 1 (BH, 3-2 faculty).
Now, we also know that R got 5 votes from non-candidates.
Now we can write 5 as
(i) 5
(ii) 4+1
(iii) 3+2
Considering case (i) 4+1. This is only possible when there is 1 candidate from OQ, and there are 2 candidates from BH. This implies that the number of candidates in FA and MQ is 1. Now, if we consider FA and MQ and put only 1 candidate there, it implies that there are 15 non-candidate voters between them. Now we know this is not possible since the maximum number of non-candidate voters a candidate can get is 13. (Please note that non-candidates of a particular department vote as a block).
On similar grounds, we can eliminate Case (iii) as it also implies there is only 1 candidate in FA and MQ.
Now, considering Case (i), we know that 5+0 will happen only one when there are 5 non-candidates in a single department. This is only possible in MS (Out of 7, there will be 2 candidates and 5 non-candidates).
So we can conclude that MS has 2 candidates and that they voted Prof. R…….(i)
We also know that Prof P got 2 votes from Non-candidates. This is only possible when BH has 1 candidate.
So, we can conclude that the number of professors in FA, MS, OQ, BH is 0,2,1,1
Thus, we get the following table:
Now, if we consider Department MS, we know that there are 2 candidates from MS and R can’t be one of them as the people in that department voted for him….. (3 rd condition).
So the possible combinations of candidates in MS are (P,Q), (Q,S), (P,S).
Now we also know that no one can vote for a candidate in their own department, so we can eliminate (P,S) and (Q,S) as we know that S voted for P and Q voted for S).
So we can infer that P and Q are from MS.
Since Prof Qureshi belongs to MS, non-candidates from MS can't vote for him. We can see that the non-candidates from FA voted for him. So, only statement B is true. Therefore, the correct answer is Option B.
Passage - 2
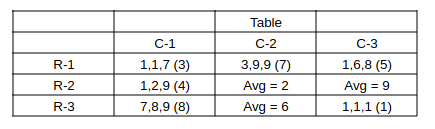
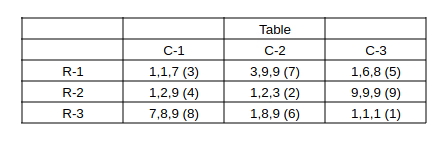
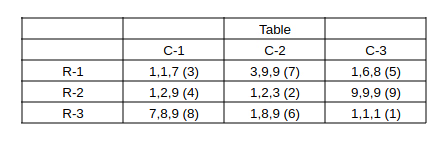
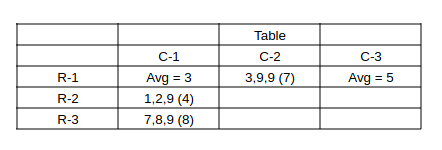
There are nine boxes arranged in a 3 × 3 array as shown in Tables 1 and 2. Each box contains three sacks. Each sack has a certain number of coins, between 1 and 9, both inclusive.
The average number of coins per sack in the boxes are all distinct integers. The total number of coins in each row is the same. The total number of coins in each column is also the same.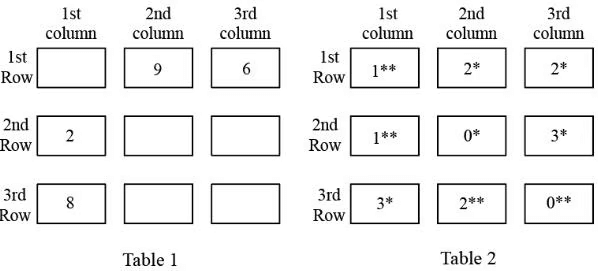
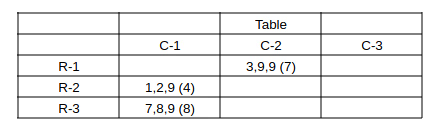
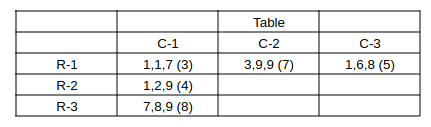
Table 1 gives information regarding the median of the numbers of coins in the three sacks in a box for some of the boxes.
In Table 2 each box has a number which represents the number of sacks in that box having more than 5 coins. That number is followed by a * if the sacks in that box satisfy exactly one among the following three conditions, and it is followed by ** if two or more of these conditions are satisfied.
(i) The minimum among the numbers of coins in the three sacks in the box is 1.
(ii) The median of the numbers of coins in the three sacks is 1.
(iii) The maximum among the numbers of coins in the three sacks in the box is 9.
Q1: What is the total number of coins in all the boxes in the 3rd row?
(a) 36
(b) 30
(c) 15
(d) 45
Ans: d
Sol: We are given that each box contains three sacks. Each sack has a certain number of coins, between 1 and 9, both inclusive.
The average number of coins per sack in the boxes are all distinct integers. The total number of coins in each row is the same. The total number of coins in each column is also the same.
=> The total number of coins in a box range from 3 (1 + 1 + 1) to 27 (9 + 9 + 9)
Since, it is given that the average number of coins per sack in the boxes are all distinct integers => The total number of coins in a box would be 3, 6, 9, 12, 15, 18, 21, 24, 27 => averages of 1, 2, 3, 4,....,9 => Sum = 45.
=> Sum of averages coins in a box in a row or column = 45/3 = 15 [The total number of coins in each row is the same. The total number of coins in each column is also the same.] ==> (1)
Let us represent the final configuration of the sacks in boxes as follows:
Also a bag (x,y) => bag in xth row and yth column.
We are given 2 clues => Table-1 & Table-2
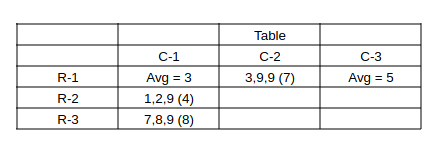
Consider bag (3,1)
=> From Table-1 => Median = 8 & From Table-2 all 3 sacks have more than 5 coins. Also * => There is a 9 in one of the sacks.
=> c, 8, 9 are the coins in bag (3,1), now c > 5 & c + 8 + 9 should be a multiple of 3 => c = 7 is the only possiblility.
=> bag (3,1) has 7, 8, 9 coins with average = 8.
Consider bag (2,1)
Median = 2 and 1 sack has more than 5 coins. Also ** => conditions i & iii should be satisfied.
=> 1, 2, 9 are the coins in bag (2,1) with average = 4
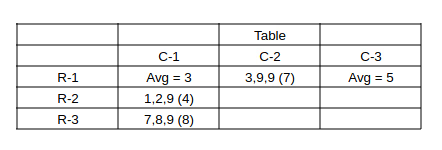
Consider bag (1,2)
Median = 9 and 2 elements are more than 5. Also * => (9 is present & 1 is not present)
=> c, 9, 9 are the coins in bag (1,2) and c is not equal to 1 and less than 5 => c = 3 for c + 18 to be a multiple of 3.
=> 3, 9, 9 are the coins in bag (1,2) with average = 7.
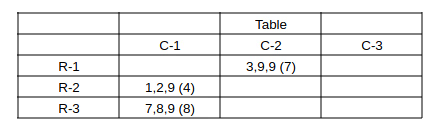
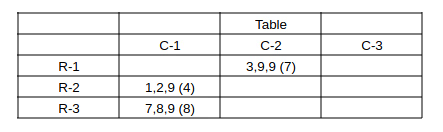
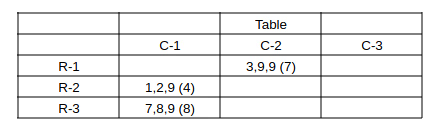
Capturing this info. in the table:
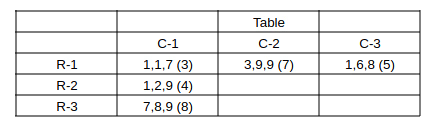
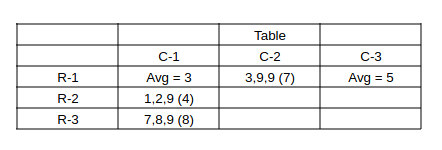
From (1), The average in bag (1,1) is 15 - 4 - 8 = 3.
From (1), The average in bag (1,3) is 15 - 3 - 7 = 5.
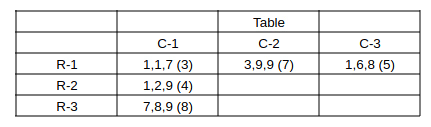
Consider bag (1,1)
Avg = 3, 1 sack has more than 5 and ** => 2 conditions are being satisfied. => (can't be condition-3 => 9 coins as the total sum of coins is it self 3*3 = 9)
=> bag (1,1) has 1, 1, 7 coins with average = 3.
Consider bag (1,3)
Avg. = 5 => Sum = 15.
Median = 6 and 2 sacks have more than 5 and * => (1 condition is satisfied)
Not condition ii as the median is 6 & Not condition iii as the sum of 2 sacks itself will become 6 + 9 = 15
=> 1, 6, c are the coins => For sum = 15 => c = 15 - 1 - 6 = 8
=> bag (1,3) has 1, 6, 8 coins with average = 5.
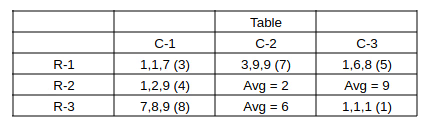
Consider bag (3,3)
0 sacks have more than 5 coins and ** => conditions i & ii are being satisfied.
=> 1,1,c are the coins. Now c = 1 or 2 or 3 or 4 => c = 1 or 4 for number of coins to be a multiple of 3.
But c = 1 as no other bag has the possibility to get avg. = 1 as bag (2,2) should have 1, b, c coins and b and c should be more than 1 as only 1*
=> bag (3,3) has 1, 1, 1 coins with average = 1.
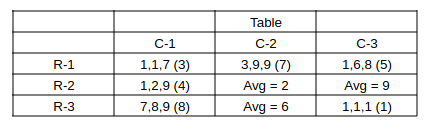
Now, we can fill the averages in all the bags.
In bag (2,3) Avg. = 9 => 9, 9, 9 are the coins.
In bag (2,2) => Avg. = 2 => Sum = 6 and only 1* => smallest elemens=t should be 1.
=> 1, b, c are the coins where b + c = 5 and b,c can't be equal to 1 and less than 5 => 2 + 3 = 5 is the only possibility.
=> 1, 2, 3 are the coins with average = 2.
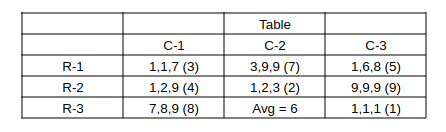
Considering bag (3,2)
Avg. = 6 => Sum = 18.
2 sacks more than 5 coins and ** => 2 sacks have 1 and 9 coins.
=> bag (3,2) has 1, c, 9 coins and c = 18 - 1 - 9 = 8
=> bag (3,2) has 1, 8, 9 coins with average = 6 coins.
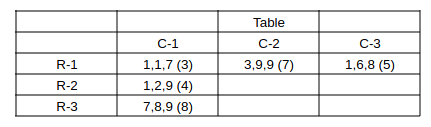
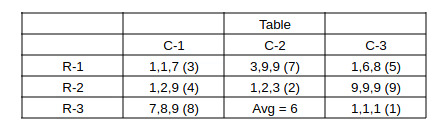
==> Final required table, bracket number => average coins per sack in the bag.
Sum of coins in 3rd row = 8*3 + 6*3 + 1*3 = 45.
Q2: How many boxes have at least one sack containing 9 coins?
(a) 3
(b) 4
(c) 5
(d) 8
Ans: c
Sol: We are given that each box contains three sacks. Each sack has a certain number of coins, between 1 and 9, both inclusive.
The average number of coins per sack in the boxes are all distinct integers. The total number of coins in each row is the same. The total number of coins in each column is also the same.
=> The total number of coins in a box range from 3 (1 + 1 + 1) to 27 (9 + 9 + 9)
Since, it is given that the average number of coins per sack in the boxes are all distinct integers => The total number of coins in a box would be 3, 6, 9, 12, 15, 18, 21, 24, 27 => averages of 1, 2, 3, 4,....,9 => Sum = 45.
=> Sum of averages coins in a box in a row or column = 45/3 = 15 [The total number of coins in each row is the same. The total number of coins in each column is also the same.] ==> (1)
Let us represent the final configuration of the sacks in boxes as follows:
Also a bag (x,y) => bag in xth row and yth column.
We are given 2 clues => Table-1 & Table-2
Consider bag (3,1)
=> From Table-1 => Median = 8 & From Table-2 all 3 sacks have more than 5 coins. Also * => There is a 9 in one of the sacks.
=> c, 8, 9 are the coins in bag (3,1), now c > 5 & c + 8 + 9 should be a multiple of 3 => c = 7 is the only possiblility.
=> bag (3,1) has 7, 8, 9 coins with average = 8.
Consider bag (2,1)
Median = 2 and 1 sack has more than 5 coins. Also ** => conditions i & iii should be satisfied.
=> 1, 2, 9 are the coins in bag (2,1) with average = 4
Consider bag (1,2)
Median = 9 and 2 elements are more than 5. Also * => (9 is present & 1 is not present)
=> c, 9, 9 are the coins in bag (1,2) and c is not equal to 1 and less than 5 => c = 3 for c + 18 to be a multiple of 3.
=> 3, 9, 9 are the coins in bag (1,2) with average = 7.
Capturing this info. in the table:
From (1), The average in bag (1,1) is 15 - 4 - 8 = 3.
From (1), The average in bag (1,3) is 15 - 3 - 7 = 5.
Consider bag (1,1)
Avg = 3, 1 sack has more than 5 and ** => 2 conditions are being satisfied. => (can't be condition-3 => 9 coins as the total sum of coins is it self 3*3 = 9)
=> bag (1,1) has 1, 1, 7 coins with average = 3.
Consider bag (1,3)
Avg. = 5 => Sum = 15.
Median = 6 and 2 sacks have more than 5 and * => (1 condition is satisfied)
Not condition ii as the median is 6 & Not condition iii as the sum of 2 sacks itself will become 6 + 9 = 15
=> 1, 6, c are the coins => For sum = 15 => c = 15 - 1 - 6 = 8
=> bag (1,3) has 1, 6, 8 coins with average = 5.
Consider bag (3,3)
0 sacks have more than 5 coins and ** => conditions i & ii are being satisfied.
=> 1,1,c are the coins. Now c = 1 or 2 or 3 or 4 => c = 1 or 4 for number of coins to be a multiple of 3.
But c = 1 as no other bag has the possibility to get avg. = 1 as bag (2,2) should have 1, b, c coins and b and c should be more than 1 as only 1*
=> bag (3,3) has 1, 1, 1 coins with average = 1.
Now, we can fill the averages in all the bags.
In bag (2,3) Avg. = 9 => 9, 9, 9 are the coins.
In bag (2,2) => Avg. = 2 => Sum = 6 and only 1* => smallest elemens=t should be 1.
=> 1, b, c are the coins where b + c = 5 and b,c can't be equal to 1 and less than 5 => 2 + 3 = 5 is the only possibility.
=> 1, 2, 3 are the coins with average = 2.
Considering bag (3,2)
Avg. = 6 => Sum = 18.
2 sacks more than 5 coins and ** => 2 sacks have 1 and 9 coins.
=> bag (3,2) has 1, c, 9 coins and c = 18 - 1 - 9 = 8
=> bag (3,2) has 1, 8, 9 coins with average = 6 coins.
==> Final required table, bracket number => average coins per sack in the bag.
Bags (2,1), (3,1), (1,2), (3,2), (2,3) have at least 1 sack with 9 coins. => Total of 5 bags.
Q3: For how many boxes are the average and median of the numbers of coins contained in the three sacks in that box the same?
Ans: 4
Sol: We are given that each box contains three sacks. Each sack has a certain number of coins, between 1 and 9, both inclusive.
The average number of coins per sack in the boxes are all distinct integers. The total number of coins in each row is the same. The total number of coins in each column is also the same.
=> The total number of coins in a box range from 3 (1 + 1 + 1) to 27 (9 + 9 + 9)
Since, it is given that the average number of coins per sack in the boxes are all distinct integers => The total number of coins in a box would be 3, 6, 9, 12, 15, 18, 21, 24, 27 => averages of 1, 2, 3, 4,....,9 => Sum = 45.
=> Sum of averages coins in a box in a row or column = 45/3 = 15 [The total number of coins in each row is the same. The total number of coins in each column is also the same.] ==> (1)
Let us represent the final configuration of the sacks in boxes as follows:
Also a bag (x,y) => bag in xth row and yth column.
We are given 2 clues => Table-1 & Table-2
Consider bag (3,1)
=> From Table-1 => Median = 8 & From Table-2 all 3 sacks have more than 5 coins. Also * => There is a 9 in one of the sacks.
=> c, 8, 9 are the coins in bag (3,1), now c > 5 & c + 8 + 9 should be a multiple of 3 => c = 7 is the only possiblility.
=> bag (3,1) has 7, 8, 9 coins with average = 8.
Consider bag (2,1)
Median = 2 and 1 sack has more than 5 coins. Also ** => conditions i & iii should be satisfied.
=> 1, 2, 9 are the coins in bag (2,1) with average = 4
Consider bag (1,2)
Median = 9 and 2 elements are more than 5. Also * => (9 is present & 1 is not present)
=> c, 9, 9 are the coins in bag (1,2) and c is not equal to 1 and less than 5 => c = 3 for c + 18 to be a multiple of 3.
=> 3, 9, 9 are the coins in bag (1,2) with average = 7.
Capturing this info. in the table:
From (1), The average in bag (1,1) is 15 - 4 - 8 = 3.
From (1), The average in bag (1,3) is 15 - 3 - 7 = 5.
Consider bag (1,1)
Avg = 3, 1 sack has more than 5 and ** => 2 conditions are being satisfied. => (can't be condition-3 => 9 coins as the total sum of coins is it self 3*3 = 9)
=> bag (1,1) has 1, 1, 7 coins with average = 3.
Consider bag (1,3)
Avg. = 5 => Sum = 15.
Median = 6 and 2 sacks have more than 5 and * => (1 condition is satisfied)
Not condition ii as the median is 6 & Not condition iii as the sum of 2 sacks itself will become 6 + 9 = 15
=> 1, 6, c are the coins => For sum = 15 => c = 15 - 1 - 6 = 8
=> bag (1,3) has 1, 6, 8 coins with average = 5.
Consider bag (3,3)
0 sacks have more than 5 coins and ** => conditions i & ii are being satisfied.
=> 1,1,c are the coins. Now c = 1 or 2 or 3 or 4 => c = 1 or 4 for number of coins to be a multiple of 3.
But c = 1 as no other bag has the possibility to get avg. = 1 as bag (2,2) should have 1, b, c coins and b and c should be more than 1 as only 1*
=> bag (3,3) has 1, 1, 1 coins with average = 1.
Now, we can fill the averages in all the bags.
In bag (2,3) Avg. = 9 => 9, 9, 9 are the coins.
In bag (2,2) => Avg. = 2 => Sum = 6 and only 1* => smallest elemens=t should be 1.
=> 1, b, c are the coins where b + c = 5 and b,c can't be equal to 1 and less than 5 => 2 + 3 = 5 is the only possibility.
=> 1, 2, 3 are the coins with average = 2.
Considering bag (3,2)
Avg. = 6 => Sum = 18.
2 sacks more than 5 coins and ** => 2 sacks have 1 and 9 coins.
=> bag (3,2) has 1, c, 9 coins and c = 18 - 1 - 9 = 8
=> bag (3,2) has 1, 8, 9 coins with average = 6 coins.
==> Final required table, bracket number => average coins per sack in the bag.
Average = Median in boxes (3,1), (2,2), (2,3) and (3,3) => 4 boxes.
Q4: How many sacks have exactly one coin?
Ans: 9
Sol: We are given that each box contains three sacks. Each sack has a certain number of coins, between 1 and 9, both inclusive.
The average number of coins per sack in the boxes are all distinct integers. The total number of coins in each row is the same. The total number of coins in each column is also the same.
=> The total number of coins in a box range from 3 (1 + 1 + 1) to 27 (9 + 9 + 9)
Since, it is given that the average number of coins per sack in the boxes are all distinct integers => The total number of coins in a box would be 3, 6, 9, 12, 15, 18, 21, 24, 27 => averages of 1, 2, 3, 4,....,9 => Sum = 45.
=> Sum of averages coins in a box in a row or column = 45/3 = 15 [The total number of coins in each row is the same. The total number of coins in each column is also the same.] ==> (1)
Let us represent the final configuration of the sacks in boxes as follows:
Also a bag (x,y) => bag in xth row and yth column.
We are given 2 clues => Table-1 & Table-2
Consider bag (3,1)
=> From Table-1 => Median = 8 & From Table-2 all 3 sacks have more than 5 coins. Also * => There is a 9 in one of the sacks.
=> c, 8, 9 are the coins in bag (3,1), now c > 5 & c + 8 + 9 should be a multiple of 3 => c = 7 is the only possiblility.
=> bag (3,1) has 7, 8, 9 coins with average = 8.
Consider bag (2,1)
Median = 2 and 1 sack has more than 5 coins. Also ** => conditions i & iii should be satisfied.
=> 1, 2, 9 are the coins in bag (2,1) with average = 4
Consider bag (1,2)
Median = 9 and 2 elements are more than 5. Also * => (9 is present & 1 is not present)
=> c, 9, 9 are the coins in bag (1,2) and c is not equal to 1 and less than 5 => c = 3 for c + 18 to be a multiple of 3.
=> 3, 9, 9 are the coins in bag (1,2) with average = 7.
Capturing this info. in the table:
From (1), The average in bag (1,1) is 15 - 4 - 8 = 3.
From (1), The average in bag (1,3) is 15 - 3 - 7 = 5.
Consider bag (1,1)
Avg = 3, 1 sack has more than 5 and ** => 2 conditions are being satisfied. => (can't be condition-3 => 9 coins as the total sum of coins is it self 3*3 = 9)
=> bag (1,1) has 1, 1, 7 coins with average = 3.
Consider bag (1,3)
Avg. = 5 => Sum = 15.
Median = 6 and 2 sacks have more than 5 and * => (1 condition is satisfied)
Not condition ii as the median is 6 & Not condition iii as the sum of 2 sacks itself will become 6 + 9 = 15
=> 1, 6, c are the coins => For sum = 15 => c = 15 - 1 - 6 = 8
=> bag (1,3) has 1, 6, 8 coins with average = 5.
Consider bag (3,3)
0 sacks have more than 5 coins and ** => conditions i & ii are being satisfied.
=> 1,1,c are the coins. Now c = 1 or 2 or 3 or 4 => c = 1 or 4 for number of coins to be a multiple of 3.
But c = 1 as no other bag has the possibility to get avg. = 1 as bag (2,2) should have 1, b, c coins and b and c should be more than 1 as only 1*
=> bag (3,3) has 1, 1, 1 coins with average = 1.
Now, we can fill the averages in all the bags.
In bag (2,3) Avg. = 9 => 9, 9, 9 are the coins.
In bag (2,2) => Avg. = 2 => Sum = 6 and only 1* => smallest elemens=t should be 1.
=> 1, b, c are the coins where b + c = 5 and b,c can't be equal to 1 and less than 5 => 2 + 3 = 5 is the only possibility.
=> 1, 2, 3 are the coins with average = 2.
Considering bag (3,2)
Avg. = 6 => Sum = 18.
2 sacks more than 5 coins and ** => 2 sacks have 1 and 9 coins.
=> bag (3,2) has 1, c, 9 coins and c = 18 - 1 - 9 = 8
=> bag (3,2) has 1, 8, 9 coins with average = 6 coins.
==> Final required table, bracket number => average coins per sack in the bag.
Bag (1,1) => 2 sacks with 1 coins, (2,1) => 1 sack, (2,2) => 1 sack, (3,2) => 1 sack, (1,3) => 1 sack, (3,3) => 3 sacks.
=> Total = 2 + 1 + 1 + 1 + 1 + 3 = 9 sacks.
|
77 videos|180 docs|96 tests
|
FAQs on CAT Previous Year Questions - Team Formations - Logical Reasoning (LR) and Data Interpretation (DI)
| 1. What are some common types of team formations used in competitive exams like CAT? |  |
| 2. How can I improve my skills in solving team formation problems for the CAT exam? |  |
| 3. Are there any specific strategies for tackling team formation questions in the CAT exam? |  |
| 4. How do team formation questions impact my overall score in the CAT exam? |  |
| 5. Where can I find practice questions specifically focused on team formations for the CAT exam? |  |