Half Yearly Class 9 Mathematics Set 3 | Mathematics (Maths) Class 9 PDF Download
Time: 3 Hours
Maximum Marks: 80
General Instructions:
(i) The question paper comprises four sections: A, B, C, and D.
(ii) All questions are compulsory. However, internal choices are provided in some questions.
(iii) Section A has 10 Questions carrying 1 mark each.
(iv) Section B has 5 Questions carrying 2 marks each.
(v) Section C has 10 Questions carrying 3 marks each.
(vi) Section D has 5 Questions carrying 6 marks each.
(vii) Use of calculators is not permitted.
Section A
Q1. Is √8 rational or irrational? (1 Mark)
Q2. What is the degree of a zero polynomial? (1 Mark)
Q3. What is the y-coordinate of a point on the x-axis? (1 Mark)
Q4. If x − 2y = 4, what is y when x = 0? (1 Mark)
Q5. State Euclid’s fourth postulate. (1 Mark)
Q6. If ∠A = 60° in △ABC and AB = AC , what is ∠B? (1 Mark)
Q7. Simplify: √75. (1 Mark)
Q8. If p(−1) = 0 for p(x) = x2 + kx − 3, find k. (1 Mark)
Q9. Does the point (0, 5) lie on the x-axis or y-axis? (1 Mark)
Q10. If a transversal intersects two parallel lines, what is the sum of interior angles on the same side? (1 Mark)
Section B
Q1. Rationalize: 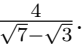 (2 Marks)
(2 Marks)
Q2. Find the product of the zeroes of x2 − 6x + 8. (2 Marks)
Q3. Find the distance between A(0, 2) and B(3, −2). (2 Marks)
Q4. Solve 4x + y = 10 for x when y = 2. (2 Marks)
Q5. If ∠X Y Z = 110° and X Y ∥ Z W, find the corresponding angle to ∠X Y Z. (2 Marks)
Section C
Q1. Prove that √2 is irrational. (3 Marks)
Q2. Find the zeroes of x2 − 3x − 10. (3 Marks)
Q3. Find the area of the triangle formed by points A(1, 2), B(4, 2), C (2, 5). (3 Marks)
Q4. Solve: x + 2y = 7 and 3x − y = 4 graphically. (3 Marks)
Q5. Using Euclid’s postulates, prove that every line segment has a unique midpoint. (3 Marks)
Q6.In △DEF, if DE ∥ FG and ∠D = 45°, find ∠EFG (3 Marks)
Q7. Find k such that 2x2 + kx + 5 has equal roots. (3 Marks)
Q8. Express 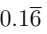 as a fraction. (3 Marks)
as a fraction. (3 Marks)
Q9. Solve: 5x − 2y = 8 and x + y = 4 using graphical method. (3 Marks)
Q10. Find the area of the triangle whose sides are 42 cm, 34 cm and 20 cm in length. Hence, find the height corresponding to the longest side. (3 Marks)
Section D
Q1. Find the quotient and remainder when x3 − 6x2 + 11x − 6 is divided by x − 1. (6 Marks)
Q2. For points A(−1, 0), B(3, 0), C (0, 4), find the area of △ABC and check if it’s isosceles. (6 Marks)
Q3. Prove that the sum of angles in a triangle is 180° using parallel lines and a transversal. (6 Marks)
Q4. Solve: x − y = 3 and 2x + y = 9 graphically. Find the area of the triangle formed by these lines and the y-axis. (6 Marks)
Q5. Solve: 4x + 3y = 14 and 2x − y = 2 using elimination method. Verify the solution. (6 Marks)
You can access the solutions to this Half Yearly here.
|
40 videos|563 docs|57 tests
|
FAQs on Half Yearly Class 9 Mathematics Set 3 - Mathematics (Maths) Class 9
| 1. What topics are typically covered in a Class 9 Half-Yearly Math exam? |  |
| 2. How can I prepare effectively for the Class 9 Half-Yearly Math exam? |  |
| 3. What is the format of the Class 9 Half-Yearly Math Question Paper? |  |
| 4. How important are previous year question papers for Class 9 Math preparation? |  |
| 5. What strategies can help in managing time during the Class 9 Half-Yearly Math exam? |  |





















