Defining and Differentiating Parametric Equations Chapter Notes | Calculus BC - Grade 9 PDF Download
| Table of contents |

|
| What Are Parametric Equations? |

|
| Differentiating Parametric Equations |

|
| Extending Differentiation to Parametric Functions |

|
| Practice Examples |

|
In Unit 9 of AP Calculus BC, we explore three fascinating topics: parametric equations, polar coordinates, and vector-valued functions. This post focuses on parametric equations, which are incredibly useful for modeling real-world phenomena like projectile motion or circular paths. Let’s dive into what makes parametric equations unique and how to differentiate them!
What Are Parametric Equations?
Parametric equations describe a relationship where the x- and y-coordinates of a point are defined independently in terms of a third variable, often called the parameter (typically t for time). Unlike the Cartesian system, where we assume steady movement along the x-axis, parametric equations offer flexibility to model complex motions, such as curves or trajectories, by allowing both coordinates to vary with t.
For example, consider the parametric equations:
x(t) = t² - 1, y(t) = 3t
Here, the x-coordinate depends on t² - 1, and the y-coordinate depends on 3t. At t = 1, you’d plot the point (0, 3) on the xy-plane. The parameter t doesn’t appear on the graph itself—it’s a tool to define the relationship between x and y independently.
There are several methods for calculating derivatives of real-valued functions, such as the limit definition, the power rule, the product rule, and the quotient rule. These methods can be extended to parametric functions, which are functions that depend on both a real variable and one or more parameters.
"To summarize, methods for calculating derivatives of real-valued functions can be extended to parametric functions."
One way to extend these methods to parametric functions is to treat the parameters as constants and use the usual rules for differentiation. For example, if a parametric function is given by f(x, p) = px2, where x is the real variable and p is the parameter, then the derivative with respect to x can be calculated using the power rule as df/dx=2p∗x.
However, our method for computing derivatives will actually be much simpler than the method above.
Differentiating Parametric Equations
Since parametric equations are graphed on the xy-plane, finding the slope of a tangent line to a parametric curve still requires calculating dy/dx. However, because x and y are both functions of t, we use a special approach. The slope of the tangent line is given by:
dy/dx = (dy/dt) / (dx/dt)
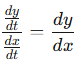 This means you take the derivative of y(t) with respect to t (denoted dy/dt) and divide it by the derivative of x(t) with respect to t (denoted dx/dt). Note that dx/dt must not equal zero, as this could indicate a vertical tangent, where the slope is undefined.
This means you take the derivative of y(t) with respect to t (denoted dy/dt) and divide it by the derivative of x(t) with respect to t (denoted dx/dt). Note that dx/dt must not equal zero, as this could indicate a vertical tangent, where the slope is undefined.This method, known as the parametric derivative, is unique to parametric equations and allows us to find the instantaneous rate of change at any point on the curve. It’s a powerful tool for analyzing motion or other dynamic systems.
Extending Differentiation to Parametric Functions
Still confused about the theory? Let's go into further detail on what this idea really means physically and mathematically.
This idea is known as the "parametric derivative" in calculus, often used to find the instantaneous rate of change of a parametric curve at a specific point. This method can only be used for parametric equations, where the curve is defined using a set of parametric equations in terms of a parameter, such as t.
To find the slope of the tangent line at a point on the curve, we first find the derivative of the x-coordinate function with respect to the parameter and the derivative of the y-coordinate function with respect to the parameter. These derivatives are denoted as dx/dt and dy/dt respectively.
Then, at a specific point on the curve (x, y) the slope of the tangent line is found by taking the ratio of the derivative of the y-coordinate function with respect to the parameter (dy/dt) to the derivative of the x-coordinate function with respect to the parameter (dx/dt). This is the equation dy/dx = dy/dt /dx/dt we saw earlier! It’s important to note that the above equation is only valid if dx/dt is not equal to zero at the point of interest, as a vertical tangent line would not have a well-defined slope.
Practice Examples
Let’s solidify our understanding with two examples of finding the slope of a tangent line for parametric equations.
Example 1: Slope at t = 3
Given the parametric equations:
x(t) = t² - 2t, y(t) = t² + 1
Find the slope of the tangent line at t = 3.
Step 1: Compute dx/dt and dy/dt.
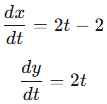
Step 2: Find dy/dx using the parametric derivative formula:
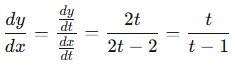
Step 3: Evaluate at t = 3:

Conclusion: The slope of the tangent line at t = 1 is 3/2.
Example 2: Slope at t = -1
Given the parametric equations:
x(t) = ln(t), y(t) = 3t⁴ + 2t⁵ + 3t - 8
Find the slope of the tangent line at t = -1.
Step 1: Compute dx/dt and dy/dt.
dx/dt = 1/t
dy/dt = 12t³ + 10t⁴ + 3
Step 2: Find dy/dx:
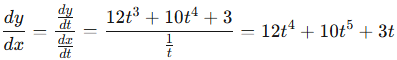
Step 3: Evaluate at t = -1:
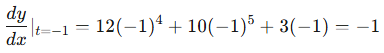
Conclusion: The slope of the tangent line at t = -1 is -1.
Key Takeaway
The first derivative of a parametric equation defined by x(t) and y(t) is:
 This formula is essential for finding the slope of a tangent line to a parametric curve, provided dx/dt ≠ 0. With practice, this concept becomes intuitive, especially if you’re comfortable with derivatives from earlier calculus units.
This formula is essential for finding the slope of a tangent line to a parametric curve, provided dx/dt ≠ 0. With practice, this concept becomes intuitive, especially if you’re comfortable with derivatives from earlier calculus units.
Key Terms to Know
- Cartesian Graph: A two-dimensional grid (xy-plane) with perpendicular x- and y-axes intersecting at the origin (0, 0), used to plot points and functions.
- Derivative: Measures the rate of change of a function at a specific point, indicating its slope or sensitivity to change.
- df/dx: The derivative of a function f with respect to x, showing the function’s rate of change or slope.
- Dummy Variable: A placeholder variable (e.g., t) used to define relationships without intrinsic meaning.
- dy/dt: The derivative of y with respect to the parameter t, measuring the rate of change of y.
- Horizontal Motion: Movement along a straight line parallel to the ground, without vertical displacement.
- Limit Definition: A mathematical approach to describe a function’s behavior as the input approaches a specific value.
- Parametric Curve: A curve defined by equations that express coordinates in terms of a parameter, allowing complex shapes.
- Parametric Equations: Equations that define coordinates as functions of a parameter, enabling representation of complex motions.
- Parameters: Variables or constants that customize mathematical relationships or objects.
- Parametric Function: A function where coordinates are defined as separate functions of a parameter, typically time.
- Power Rule: A differentiation rule stating that if f(x) = xⁿ, then f'(x) = n * xⁿ⁻¹.
- Product Rule: A rule for differentiating the product of two functions: (f * g)' = f' * g + f * g'.
- Quotient Rule: A rule for differentiating a quotient: (f/g)' = (f' * g - f * g') / g².
- Real-valued Functions: Functions that take real numbers as inputs and produce real numbers as outputs.
- Tangent Line: A line that touches a curve at one point without crossing it, used to approximate the curve’s behavior.
|
48 videos|123 docs|72 tests
|
FAQs on Defining and Differentiating Parametric Equations Chapter Notes - Calculus BC - Grade 9
| 1. What are parametric equations? |  |
| 2. How do you differentiate parametric equations? |  |
| 3. Can you extend differentiation to parametric functions? |  |
| 4. What is the significance of parametric equations in real-life applications? |  |
| 5. How can I practice problems involving parametric equations? |  |



















