Arun Sharma Summary: Percentages | Quantitative Aptitude (Quant) - CAT PDF Download
Introduction
- Percentages, representing a proportion out of 100, are indispensable for standardising data comparisons across various domains.
- Derived from the Latin per centum (by the hundred), they are widely used in business for sales and profit analysis, in economics for growth and inflation metrics, and in exams for topics like profit and loss and data interpretation.
- This chapter provides a comprehensive guide to percentages, covering definitions, formulas, calculation methods, and practical applications, supported by examples and tools like conversion tables and graphs.

Core Concepts
Percentages express a part relative to a whole, multiplied by 100. Key formulas include:
- Percentage:
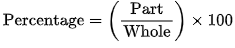
- Percentage Change:
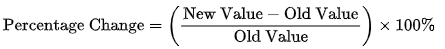
- Percentage of a Number:
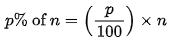
- Percentage Increase/Decrease:
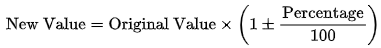
- Example: A student scoring 20 out of 50 marks has a percentage of
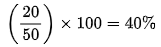
Concept of Percentage Change
Whenever the value of a measured quantity changes, the change can be captured through the following methods:
1. Absolute Value Change
- It refers to the actual change in the measured quantity.
- For instance, if sales in year one is ₹5000 crore and sales in year two is ₹6000 crore, then the absolute value of the change is ₹1000 crore.
2. Percentage Change
- It is the percentage change obtained by the formula
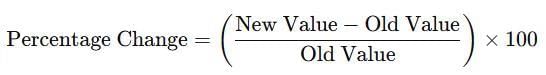
= 1000/5000 × 100 = 20%
Difference b/w Percentage Point Change and Percentage Change
- Percentage Point Change is simply the difference between the given percentages.
- But, as we have already seen, Percentage Change = (Absolute Change / Original Quantity) × 100
Example: The savings rate as a percentage of the GDP was 25% in the first year and 30% in the second year. Assume that there is no change in the GDP between the two years. Calculate the Percentage point change and the percentage change?
Sol: Percentage Point change in savings rate = 30% - 25%
= 5 percentage points.
Percentage Change in Savings = (5 / 25) × 100
= 20%
Successive Percentage Increase/Decrease
When two or more percentage changes are applied consecutively to a quantity, the percentage change is called a “successive percentage change.” The final change is not the simple addition of two or more percentages because each successive percentage is applied on the updated value.
1. Successive Increment Percentage Change
- When two or more increased percentage changes are applied consecutively, it is called a “successive increment percentage change.”
- If the population of a town increased by a% and then by b%, the first percentage, a%, is applied to the initial value; then b% is applied to the resultant value.
Example: Let the population of the town be z. Suppose the population is increased by a%, then by b%, and then by c%. What is the net percentage increase?
Sol: The first percentage increase = z + (z × a/100) = z (1 + a/100) = X
Second percentage increase = X + (X × b/100) = z (1 + a/100)(1 + b/100) = Y
Therefore, net percentage change after two increments = {(Y – z) / z} × 100
If an object x is successively increased by a%, b%, and c%, the final value is
x (1 + a/100)(1 + b/100)(1 + c/100)
2. Successive Decrement Percentage Change
- When two or more decreased percentage changes are applied consecutively, it is called a “successive decrement percentage change.”
- If the price of a product is decreased by a%, then by b%, the first percentage is applied to the initial value, then the second percentage to the result.
Example: Let the price of a product be z. If the price decreases by a%, then b%, and then c%, find the final value.
Sol: The first percentage decrease = z – (z × a/100) = z (1 – a/100) = X
Second percentage decrease = X – (X × b/100) = z (1 – a/100)(1 – b/100) = Y
Therefore, net percentage change in price after two decrements = {(Y – z) / z} × 100
If an object x is successively decreased by a%, b%, and c%, the final value is
x (1 – a/100)(1 – b/100)(1 – c/100).
3. Other Successive Percentage Changes
- Both percentage increments and decrements can be successively applied to an initial value multiple times.
- If x is successively changed by a%, b%, and c%, the final value is x (1 ± a/100)(1 ± b/100)(1 ± c/100), where + indicates increment and – indicates decrement.
4. Application of Percentage on Population Increase/Decrease:
- If there is an r% increase/decrease in the population of a place in a year, then:
- The population of a place n years later will be
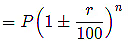
- And, the population of a place n years ago will be
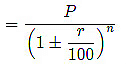
Percentage Change Graphic (PCG) and its Application
In Mathematics, percentage changes often appear in problem-solving. The following concept, the Percentage Change Graphic (PCG), is a useful visual tool for dealing with complex successive changes.
Consider an example: Increase the number 20 by 20%.
We visualise it as:
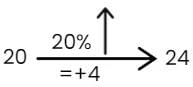
EduRev Tip: Sketch PCG on rough paper for complex successive change problems to avoid errors.
The PCG has six major applications listed and explained below:
1. Successive Changes
This is a very common situation.
Example 1: Suppose a number 30 undergoes two successive percentage increases: 20% and 10%. Find the final number after these changes.
Sol: Using PCG:
2. Product Change Application
- Suppose a product consists of two variables 10 and 10.
- If the first variable increases to 11 and the second to 12 (10% and 20% increases, respectively), what is the percentage change in the product?
(Note: 10% increase in one part and 20% in the other.) - The formula for this is A + B + AB/100.
Hence, the required percentage change = 10 + 20 + (10 × 20)/100 = 30 + 2 = 32%.
3. Product Constancy Application
Suppose the price of a commodity increases by 25%.
If total expenditure is to remain constant, by what percentage must consumption be reduced?
PCG helps us answer this.
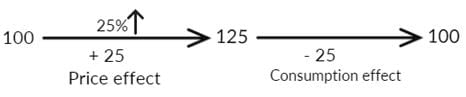
Hence, consumption must drop by 20% to offset the price increase.
4. A→B→A application
- Often, two numbers A and B are compared.
- If given the relationship A to B, the reverse relationship B to A can be estimated using PCG, similarly to product constancy.
Example: B's salary is 25% more than A's salary. By what percentage is A's salary less than B's salary?
Sol:
A drop of 25 on 125 gives a 20% drop.
Hence, A's salary is 20% less than B's.
5. Denominator Change to Ratio Change Application
- The denominator inversely affects the value of a ratio. Hence, the product constancy method applies to percentage changes in the denominator.
- For example, compare two ratios:
Ratio 1: 10/20
Ratio 2: 10/25 - The denominator increases from 20 to 25, a 25% increase.
- Ratio 1 = 0.5, Ratio 2 = 0.4.
- Percentage change between ratios = (0.1 / 0.5) × 100 = 20% drop.
- This can also be verified using PCG:
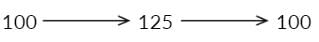 Hence, 20% drop.
Hence, 20% drop.
6. Use of PCG to Calculate Ratio Changes
- When both numerator and denominator of a ratio change, PCG offers a convenient way to calculate the net change.
1. Numerator Effect
- The numerator effect equals the percentage change in the numerator. For example, if the numerator changes from 10 to 15, i.e., a 50% increase, the numerator effect is 50%.
2. Denominator Effect
- The denominator effect is calculated by considering the reverse percentage change of the denominator. If it changes from 20 to 25, then its effect is a 20% drop when reversed.
Did You Know
- 1. If the numerator increases and denominator decreases
The ratio increases.- 2. If the numerator decreases and denominator increases
The ratio decreases.
Core Concepts
- Definition: A percentage represents a fraction with denominator 100, derived from the Latin per centum (by the hundred). It expresses proportions universally, facilitating the comparison of quantities of different scales.
- Key Formulas:
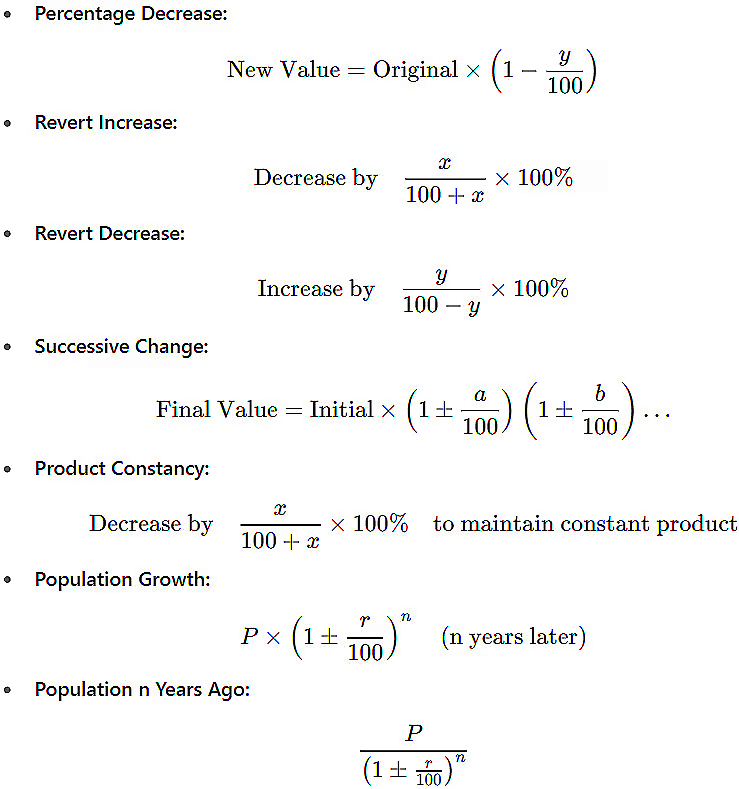
|
167 videos|238 docs|95 tests
|
FAQs on Arun Sharma Summary: Percentages - Quantitative Aptitude (Quant) - CAT
| 1. What is the definition of a percentage? |  |
| 2. How do you calculate a percentage of a number? |  |
| 3. What are some common applications of percentages in everyday life? |  |
| 4. What tools can help in calculating percentages? |  |
| 5. Why is understanding percentages important? |  |


















