Word Problems: Prime Time | Mathematics for Class 6 PDF Download
Q1: At a school event, Riya organizes a game where students say "clap" for multiples of 4 and "snap" for multiples of 6. If a number is a multiple of both, they say "clap-snap." What is the smallest number where students say "clap-snap"?
Sol: Find the least common multiple (LCM) of 4 and 6.
- Prime factorization: 4 = 2², 6 = 2 × 3.
- LCM: Take the highest power of each prime: 2² × 3 = 12.
Answer: The smallest number is 12.
Q2: Meera has 18 chocolates and 30 cookies to share equally among her friends. What is the greatest number of friends she can share them with so each gets the same number of chocolates and cookies?
Sol: Find the greatest common factor (GCF) of 18 and 30.
- Prime factorization: 18 = 2 × 3², 30 = 2 × 3 × 5.
- GCF: Take the lowest power of common primes: 2 × 3 = 6.
Answer: She can share them among 6 friends.
Q3: Vikram has 36 marbles. How many ways can he arrange them in a rectangular grid?
Sol: Find the factors of 36 (a composite number).
- Prime factorization: 36 = 2² × 3².
- Factor pairs: (1, 36), (2, 18), (3, 12), (4, 9), (6, 6).
- Each pair represents a grid (rows × columns).
Answer: There are 5 ways to arrange the marbles.
Q4: Neha has two boxes with 10 and 21 pens. Are these numbers co-prime, ensuring no equal groups (other than 1 pen) can be formed from both boxes?
Sol: Check if 10 and 21 are co-prime.
- Prime factorization: 10 = 2 × 5, 21 = 3 × 7.
- Common factors: Only 1.
- Since they share no common factors other than 1, they are co-prime.
Answer: Yes, 10 and 21 are co-prime.
Q5: Arav wants to know if 924 is divisible by 4. Can he use the divisibility rule to check?
Sol: For divisibility by 4, check the last two digits: 24.
24 ÷ 4 = 6 (no remainder).Thus, 924 is divisible by 4.
Answer: Yes, 924 is divisible by 4.
Q6: Simran has the numbers 16, 25, 29, and 49. Which is the only prime number?
Sol: Check each number:
- 16 = 2⁴ (factors: 1, 2, 4, 8, 16), composite.
- 25 = 5² (factors: 1, 5, 25), composite.
- 29 (factors: 1, 29), prime.
- 49 = 7² (factors: 1, 7, 49), composite.
Answer: The only prime number is 29.
Q7: Kavita has a set of numbers: 4, 9, 27, and 63. She wants to find out which number is a perfect cube. Which number should she choose?
Sol: Check for perfect cubes:
- 4 = 2², not a cube.
- 9 = 3², not a cube.
- 27 = 3³, a perfect cube.
- 63 = 7×9, not even a cube
Answer: 27 is the perfect cube.
Q8: Maya fills a 2x2 grid with prime numbers such that the product of the first row is 15 and the second row is 35. The first column’s product is 21, and the second column’s is 25. What are the numbers?
Sol: Grid: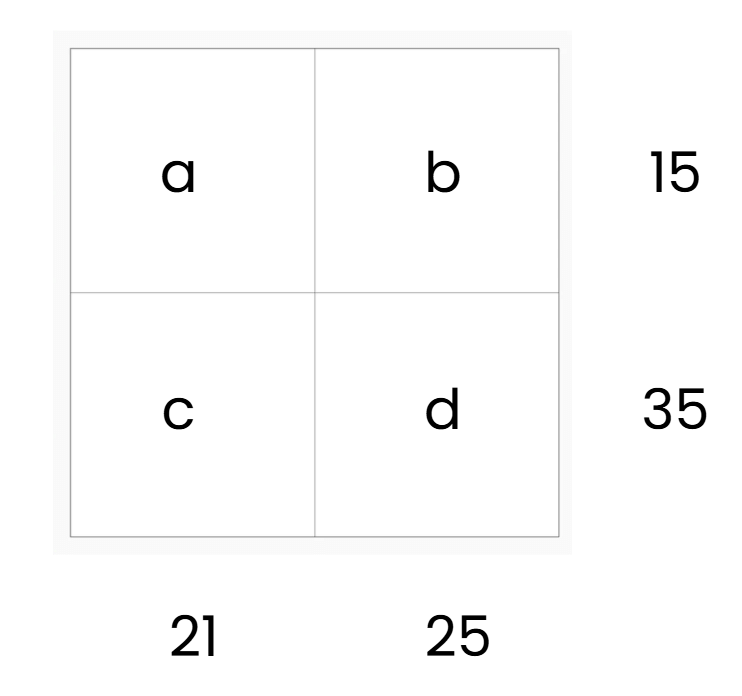
- Row 1: a × b = 15 (primes: 3 × 5).
- Row 2: c × d = 35 (primes: 5 × 7).
- Column 1: a × c = 21 (primes: 3 × 7).
- Column 2: b × d = 25 (primes: 5 × 5).
Solve:
- b = 5, d = 5 (from column 2).
- a = 3 (from row 1, since b = 5).
- c = 7 (from column 1, since a = 3).
- Check row 2: c × d = 7 × 5 = 35, correct.
Grid: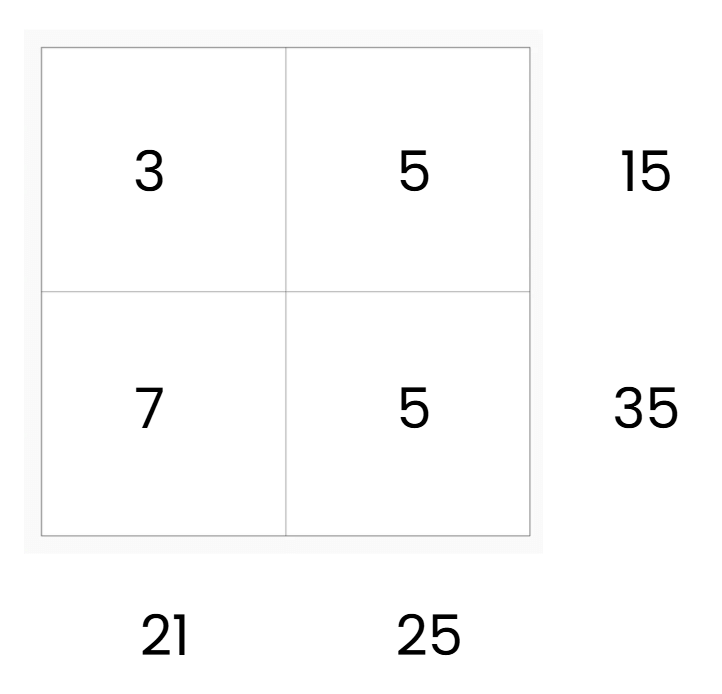
Answer: The numbers are 3, 5, 7, 5.
Q9: In a game, players say "buzz" for multiples of 7 and "fizz" for multiples of 8. What are the first three numbers where players say "buzz-fizz"?
Solution: Find the common multiples of 7 and 8 (LCM).
Prime factorization: 7 = 7, 8 = 2³.
LCM: 7 × 8 = 56. Multiples: 56, 112, 168.
Answer: The first three numbers are 56, 112, and 168.
Q10: Nidhi checks if 45 and 72 are co-prime using prime factorization. Are they co-prime?
Sol: Prime factorization: 45 = 3² × 5, 72 = 2³ × 3².
Common factors: 3² = 9.
Since they share a factor other than 1, they are not co-prime.
Answer: No, 45 and 72 are not co-prime.
Q11: Lila is checking the number 1234. She wants to know if it is divisible by 4 and 2. Is 1234 divisible by both 4 and 2?
Sol:
- Divisibility by 4: Last two digits are 34; 34 ÷ 4 = 8.5 (not an integer).
- Divisibility by 2: Last digit is 4 (even), so divisible.
Answer: 1234 is divisible by 2 but not by 4, so it is not divisible by both.
Q12: Anika arranges 60 books on shelves. Each shelf holds a number of books that is a factor of 60. How many possible shelf sizes are there?
Sol: Find the factors of 60.
Prime factorization: 60 = 2² × 3 × 5.
Number of factors: (2 + 1)(1 + 1)(1 + 1) = 3 × 2 × 2 = 12.
Answer: There are 12 possible shelf sizes.
Q13: Kavi uses the Sieve of Eratosthenes to find prime numbers from 1 to 20. How many prime numbers are there?
Solution: Use the Sieve:
- Since, 1 is not a prime number. So, Start with numbers 2 to 20.
- Circle 2, cross out multiples: 4, 6, 8, ..., 20.
- Circle 3, cross out multiples: 9, 15, 18.
- Circle 5, cross out 10, 20 (already crossed).
- Circle 7, 11, 13, 17, 19 (no multiples left).
- Primes: 2, 3, 5, 7, 11, 13, 17, 19.
Answer: There are 8 prime numbers.
Q14: Arjun sets up two alarms: one rings every 9 minutes, and the other every 12 minutes. If they start together at 8:00 AM, when will they ring together again?
Sol: Find the LCM of 9 and 12.
Prime factorization: 9 = 3², 12 = 2² × 3.
LCM: 2² × 3² = 4 × 9 = 36 minutes.
Add 36 minutes to 8:00 AM: 8:36 AM.
Answer: They ring together again at 8:36 AM.
Q15: Kunal wants to cut two ribbons of lengths 24 cm and 36 cm into equal pieces with no remainder. What is the longest possible length of each piece?
Sol: Find the Greatest Common Factor of 24 and 36.
- Prime factorization: 24 = 2³ × 3, 36 = 2² × 3².
- Greatest Common Factor: 2² × 3 = 12.
Answer: The longest length is 12 cm.
|
48 videos|334 docs|23 tests
|
FAQs on Word Problems: Prime Time - Mathematics for Class 6
| 1. What are some effective strategies for solving word problems in math? |  |
| 2. How can I improve my skills in solving prime number-related word problems? |  |
| 3. Are there any common types of word problems involving prime numbers? |  |
| 4. What resources can I use to find more practice problems on word problems and prime numbers? |  |
| 5. How important are word problems in understanding mathematical concepts, especially primes? |  |






















