Practice Questions: Playing with Constructions | Mathematics for Class 6 PDF Download
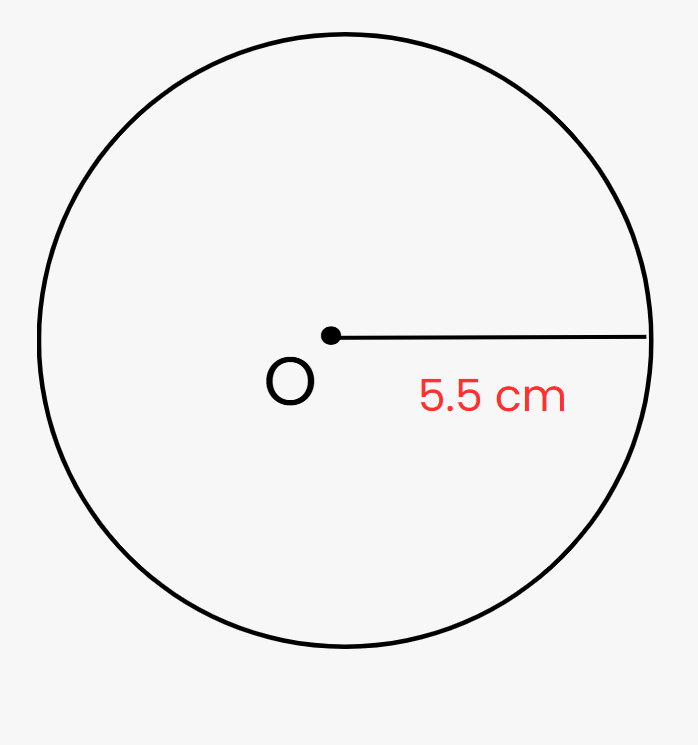
Q1: Using only a compass, draw a circle of radius 5.5 cm. Mark its center as point O.
Sol:
- Place the compass at a fixed point O.
- Open the compass to 5.5 cm using a ruler.
- Draw a full circle. This is the required circle of radius 5.5 cm.
Q2: What is the definition of a radius? Give an example using a circle.
Sol: A radius is the distance from the center of a circle to any point on its boundary.
Example: In a circle with center M and point A on the circle, MA is the radius.
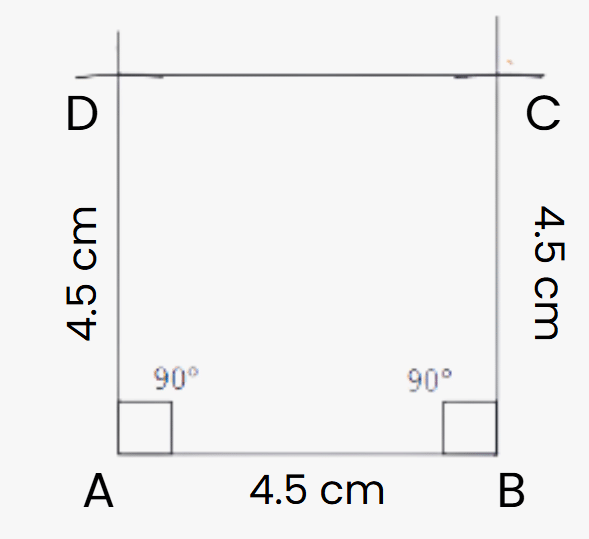
Q3: Draw a square with side 4.5 cm using only a ruler and compass.
Sol:
Draw base AB = 4.5 cm.
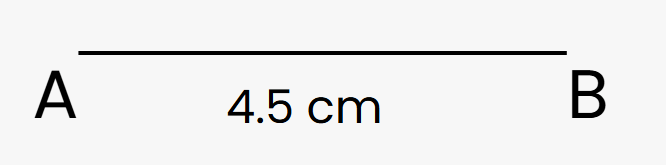
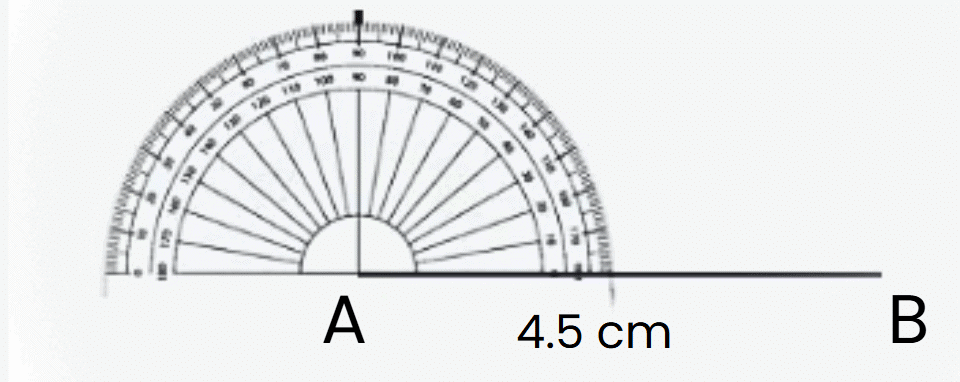
Construct 90° angles at A and B.
Using a ruler, mark point D on the perpendicular line such that AB = 4.5 cm.
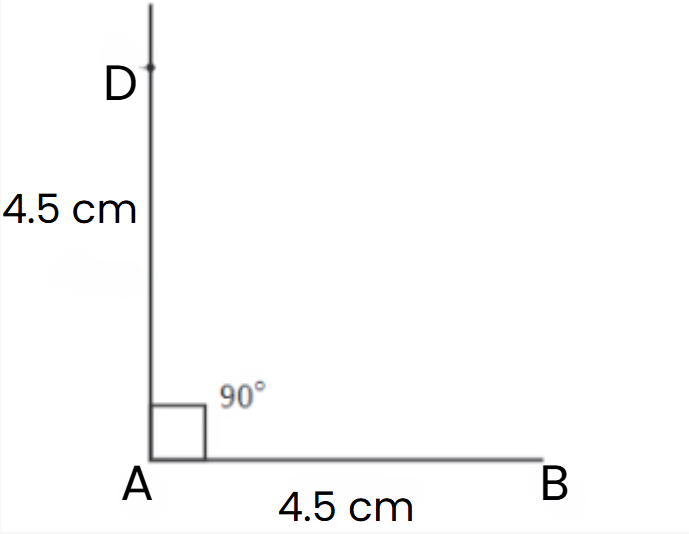
You can also use a compass to measure AD.
- Draw a perpendicular line to line segment AB at point B.
- If using a compass, the next point can be easily marked with it.
- Complete the square by ensuring all sides are equal.
Q4: What are the properties of a rectangle?
Sol:
- Opposite sides are equal and parallel.
- All four angles are 90°.
- Diagonals are equal and bisect each other.
Q5: Construct a rectangle PQRS such that PQ = 6 cm and QR = 4 cm.
Sol:
- Draw PQ = 6 cm.
- Construct perpendiculars at P and Q using a compass.
- Mark S on the perpendicular at P such that PS = 4 cm.
- Mark R on the perpendicular at Q such that QR = 4 cm.
- Join S to R, ensuring SR is parallel to PQ by using the compass to maintain equal lengths.
Same process can be done as in Q3 we did.
Q6: Construct a perpendicular bisector of a line segment AB = 7 cm.
Sol:
- Draw AB = 7 cm.
- With compass on A and B, draw arcs above and below AB using radius > 3.5 cm. ( Choose a radius greater than half of AB (3.5 cm) to ensure the arcs intersect above and below the line.)
- Connect arc intersections. This line is the perpendicular bisector.
Q7: In a square WXYZ, if WX = 6 cm, what is the length of diagonal WZ?
Sol:
Diagonal = side × √2 = 6 × √2 ≈ 6 × 1.41 = 8.46 cm
Q8: Construct a right angle using only compass and ruler.
Sol:
- Draw line AB.
- Place the compass at B, draw an arc intersecting AB at P.
- From P, draw an arc with the same radius.
- From B, draw another arc with a slightly larger radius to intersect the previous arc at Q.
- Join B to Q to form a 90° angle.
Diagram draw on your own by following the above given steps.
Q9: A photo frame is square-shaped with a side of 12 cm. What is the length of its diagonal?
Sol: Diagonal = 12 × √2 ≈ 16.97 cm.
Q10: Draw a circle of diameter 8 cm. What is its radius?
Sol: Radius = Diameter ÷ 2 = 4 cm.
Draw the circle with radius 4 cm.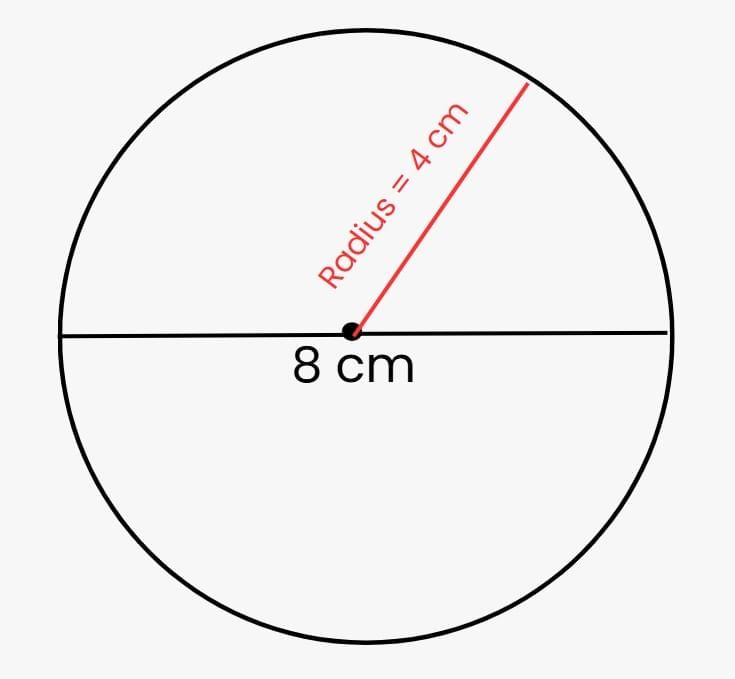
|
48 videos|334 docs|23 tests
|
FAQs on Practice Questions: Playing with Constructions - Mathematics for Class 6
| 1. What are constructions in mathematics? |  |
| 2. Why is it important to learn constructions in Class 6? |  |
| 3. What tools are commonly used for geometric constructions? |  |
| 4. Can you give an example of a simple geometric construction? |  |
| 5. How can students practice constructions at home? |  |






















