Numbers (Class 4 Mathematics ICSE) Chapter Notes | Mathematics Class 4 ICSE PDF Download
| Table of contents |

|
| Introduction |

|
| Number System |

|
| Comparison of Numbers |

|
| Predecessor and Successor |

|
| Ordering of Numbers |

|
| Forming Numbers |

|
| Even and Odd Numbers |

|
| Rounding Off Numbers |

|
Introduction
Numbers are like the magic keys that unlock the world of mathematics! In this exciting chapter, we explore large numbers, learning how to read, write, and play with them in both the Indian and the International number systems. From understanding place values to arranging numbers in order, this chapter helps us master the art of handling big numbers. We'll also learn how to create the biggest and smallest numbers, compare them, and round them off for quick estimates. Let’s dive into the adventure of numbers and discover their secrets step by step!

Number System
- Two systems are used to read and write large numbers: Indian and International.
- Indian system is used in India, grouping numbers into periods like ones, thousands, and lakhs.
- International system is used worldwide, grouping numbers into ones, thousands, and millions.
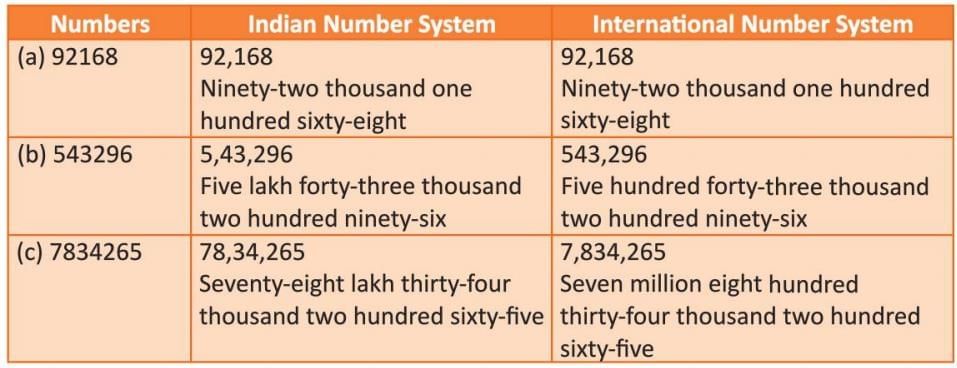
- Example: The number 137546 in the Indian system is written as 1,37,546 and read as one lakh thirty-seven thousand five hundred forty-six. In the International system, 8137546 is written as 8,137,546 and read as eight million one hundred thirty-seven thousand five hundred forty-six.
Indian Number System
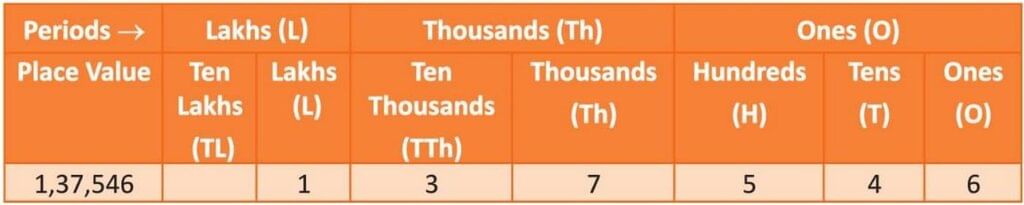
- Numbers are grouped into periods for easy reading.
- Start from the right, grouping three digits (ones, tens, hundreds) as the ones period.
- Next two digits form the thousands period (thousands, ten thousands).
- Next digits form the lakhs period (lakhs, ten lakhs).
- Commas separate periods: first after three digits from the right, then every two digits.
- Example: For 398104, group as 3,98,104. It is read as three lakh ninety-eight thousand one hundred four.
International Number System
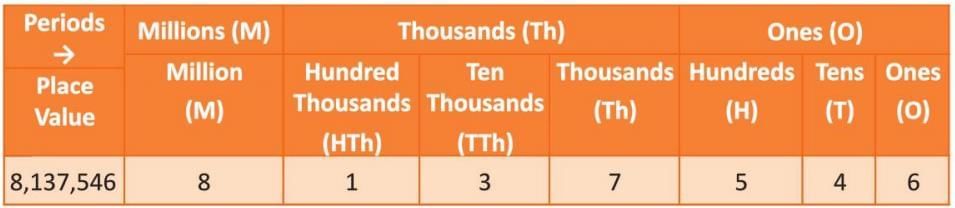
- Numbers are grouped into periods of three digits.
- First group (from right) is the ones period (ones, tens, hundreds).
- Second group is the thousands period (thousands, ten thousands, hundred thousands).
- Third group is the millions period (millions, ten millions, hundred millions).
- Commas are placed after every three digits from the right.
- Example: For 619807, group as 619,807. It is read as six hundred nineteen thousand eight hundred seven.
Comparing Indian and International Number System
- Indian system uses periods: ones, thousands, lakhs, crores.
- International system uses periods: ones, thousands, millions.
- Place values differ: e.g., 1,00,000 is one lakh (Indian) but one hundred thousand (International).
- Number names vary for large numbers due to different period names.
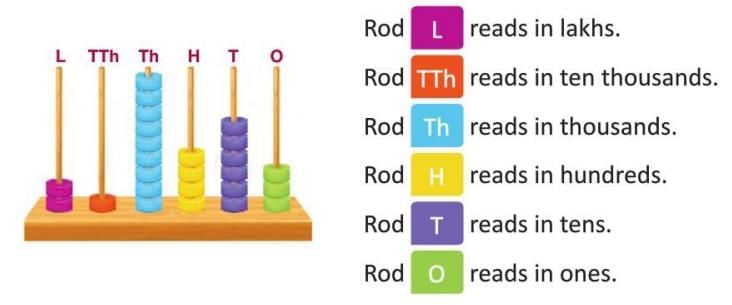
Representing Numbers on an Abacus
- An abacus shows digits on rods representing place values (lakhs, ten thousands, thousands, hundreds, tens, ones).
- Each rod shows the number of beads corresponding to the digit in that place.
- Helps visualise the value of each digit in a number.
- Example: For 2,19,463, the abacus shows 2 beads on lakhs rod, 1 on ten thousands, 9 on thousands, 4 on hundreds, 6 on tens, and 3 on ones.
Place Value and Face Value
- Place value is the value of a digit based on its position in a number.
- Face value is the digit itself, regardless of its position.
- To find place value, multiply the digit by its place (e.g., 3 in thousands place is 3 × 1000 = 3000).
- Face value remains the same as the digit (e.g., 3 is always 3).
- Example: In 5,43,296, the face value of 3 is 3, and its place value is 3 thousands or 3,000.
Expanded Form and Standard (Short) Form
- Expanded form shows a number as the sum of place values of its digits.
- Can be written in numbers (e.g., 70,000 + 8,000) or words (e.g., 7 ten thousands + 8 thousands).
- Standard form is the usual way of writing a number (e.g., 78,168).
- To convert expanded to standard, write each digit in its correct place.
- Example: For 5,08,986, expanded form is 5,00,000 + 8,000 + 900 + 80 + 6 or 5 lakhs + 8 thousands + 9 hundreds + 8 tens + 6 ones.
Comparison of Numbers
Comparing numbers helps determine which is larger or smaller.
Two methods
1. Comparison of Numbers with Different Number of Digits
- A number with more digits is always larger.
- Compare the count of digits first.
- Example: Compare 1,34,791 (6 digits) and 28,264 (5 digits). Since 6 digits > 5 digits, 1,34,791 > 28,264.
2. Comparison of Numbers with the Same Number of Digits
- Compare digits from left to right (highest place value first).
- If digits in a place are the same, move to the next place.
- Continue until a difference is found to decide which number is larger.
- Example: Compare 8,70,654 and 8,72,721. Lakhs and ten thousands are same (8 and 7). Thousands place: 0 < 2, so 8,70,654 < 8,72,721.
Predecessor and Successor
- Predecessor is the number just before (number - 1).
- Successor is the number just after (number + 1).
- Example: For 2,45,304, predecessor is 2,45,304 - 1 = 2,45,303, and successor is 2,45,304 + 1 = 2,45,305.
Ordering of Numbers
- Arrange numbers in ascending order (smallest to largest).
- Arrange numbers in descending order (largest to smallest).
- Use comparison methods to sort numbers.
- Example: For 74,328; 28,537; 76,240; 3,43,200; 29,643, ascending order is 28,537 < 29,643 < 74,328 < 76,240 < 3,43,200, and descending order is 3,43,200 > 76,240 > 74,328 > 29,643 > 28,537.
Forming Numbers
- Create numbers by arranging given digits in different orders.
- Largest number: arrange digits in descending order.
- Smallest number: arrange digits in ascending order, ensuring no leading zero.
- Repeating digits may be allowed as specified.
- Example: Using digits 9, 3, 4, 3, 7, 5, the smallest 6-digit number is 3,34,579, and the largest is 9,75,433.
Even and Odd Numbers
- Even numbers end in 0, 2, 4, 6, or 8.
- Odd numbers end in 1, 3, 5, 7, or 9.
- Check the ones place to determine if a number is even or odd.
- Example: 43,280 ends in 0 (even), and 7,981 ends in 1 (odd).
Rounding Off Numbers
Rounding gives an approximate value of a number. Round to nearest 10, 100, or 1,000 based on specific rules.
Rounding Off to the Nearest 10
- Look at the ones place digit.
- If 4 or less, keep ones place as 0, other digits unchanged.
- If 5 or more, set ones place to 0, add 1 to tens place.
- Example: 2,354 rounds to 2,350 (ones digit 4 ≤ 4). 30,795 rounds to 30,800 (ones digit 5 ≥ 5).
Rounding Off to the Nearest 100
- Look at the tens place digit.
- If 4 or less, set tens and ones to 0, keep other digits.
- If 5 or more, set tens and ones to 0, add 1 to hundreds place.
- Example: 4,768 rounds to 4,800 (tens digit 6 ≥ 5). 2,80,934 rounds to 2,80,900 (tens digit 3 ≤ 4).
Rounding Off to the Nearest 1,000
- Look at the hundreds place digit.
- If 4 or less, set hundreds, tens, and ones to 0, keep other digits.
- If 5 or more, set hundreds, tens, and ones to 0, add 1 to thousands place.
- Example: 6,578 rounds to 7,000 (hundreds digit 5 ≥ 5). 24,352 rounds to 24,000 (hundreds digit 3 ≤ 4).
|
82 docs|14 tests
|
FAQs on Numbers (Class 4 Mathematics ICSE) Chapter Notes - Mathematics Class 4 ICSE
| 1. What is the number system and why is it important in mathematics? |  |
| 2. How do we find the predecessor and successor of a number? |  |
| 3. What are even and odd numbers? |  |
| 4. How do we round off numbers and why is it useful? |  |
| 5. What is the significance of ordering numbers? |  |















