Division Chapter Notes | Mathematics Class 4 ICSE PDF Download
Introduction
Imagine you have a big box of chocolates that you want to share equally with your friends. How do you make sure everyone gets the same number of chocolates? That's where division comes in! Division is like splitting things into equal parts, whether it's sharing snacks, organising toys, or solving fun math problems. In division, the number you start with is called the dividend, the number you divide by is the divisor, and the answer you get is the quotient. In this chapter, we'll explore how to divide numbers using different methods, understand how division connects to multiplication, and even learn how to solve real-life problems. Get ready to dive into the world of division and make sharing fair and fun!

Division by Equal Sharing and Equal Grouping
- Division helps split a total quantity into equal parts.
- Equal sharing finds how many items each group gets.
- Equal grouping finds how many groups can be made.

- Steps for equal sharing:
- Identify the total quantity (dividend).
- Determine the number of groups (divisor).
- Distribute the items equally to find the number per group (quotient).
- Steps for equal grouping:
- Identify the total quantity (dividend).
- Determine the number of items per group (divisor).
- Calculate how many groups can be formed (quotient).
Example:
Kinjal wants to treat 3 friends on her birthday with 12 pastries. How many pastries will each friend get?
- Total pastries = 12 (dividend).
- Number of friends = 3 (divisor).
- Distribute one pastry to each friend: 12 - 3 = 9 pastries left.

- Distribute another pastry to each: 9 - 3 = 6 pastries left.

- Distribute another pastry to each: 6 - 3 = 3 pastries left.

- Distribute one more pastry to each: 3 - 3 = 0 pastries left.

- Each friend gets 4 pastries (12 ÷ 3 = 4, quotient).
Division as Repeated Subtraction
- Division can be done by subtracting the divisor from the dividend repeatedly until zero or less than the divisor remains.
- The number of subtractions is the quotient.
- Steps for repeated subtraction:
- Start with the dividend.
- Subtract the divisor repeatedly.
- Count how many times you subtracted to get the quotient.
Example:
There are 12 ice cubes in a tray. If 2 ice cubes are put in each glass, how many glasses are needed?
- Start with 12 ice cubes (dividend).
- Subtract 2 (divisor) for the first glass: 12 - 2 = 10.
- Subtract 2 for the second glass: 10 - 2 = 8.
- Subtract 2 for the third glass: 8 - 2 = 6.
- Subtract 2 for the fourth glass: 6 - 2 = 4.
- Subtract 2 for the fifth glass: 4 - 2 = 2.
- Subtract 2 for the sixth glass: 2 - 2 = 0.
- 6 subtractions were made, so 6 glasses are needed (12 ÷ 2 = 6, quotient).
Division Facts
- Dividing a number by 1 gives the number itself.
- Dividing a number by itself gives 1.
- Dividing zero by any number gives 0.
- Numbers ending in 0 can be divided by 10.
- Dividing any number by 0 is not possible.
Example:
- 12 ÷ 1 = 12 (number divided by 1 is the number itself).
- 19 ÷ 19 = 1 (number divided by itself is 1).
- 0 ÷ 79 = 0 (zero divided by any number is 0).
- 50 ÷ 10 = 5 (number ending in 0 divided by 10).
Multiplication and Division Facts
- Every division fact has two related multiplication facts.
- Every multiplication fact has two related division facts.
- Steps to find multiplication facts from a division fact:
- Use the quotient and divisor to form two multiplication equations.
- Multiply the divisor by the quotient to get the dividend.
- Steps to find division facts from a multiplication fact:
- Use the product as the dividend.
- Use each factor as a divisor to form two division equations.
Example:
For 30 ÷ 6 = 5, find the multiplication facts.
- From 30 ÷ 6 = 5, the quotient is 5, divisor is 6, and dividend is 30.
- First multiplication fact: 5 × 6 = 30.
- Second multiplication fact: 6 × 5 = 30.
Long Division
- Long division is used to divide large numbers systematically.
- Requires knowledge of multiplication tables and division facts.
- Steps for long division:
- Start with the leftmost digit(s) of the dividend that are divisible by the divisor.
- Find how many times the divisor fits into these digits.
- Write the result in the quotient, multiply, subtract, and bring down the next digit.
- Repeat until all digits are used.
Example:
Divide 63 by 3.
- Step 1: Take 6 tens (first digit). 6 ÷ 3 = 2 tens. Write 2 in the tens place of quotient.
- Multiply: 3 × 2 = 6. Subtract: 6 - 6 = 0.
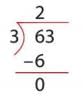
- Step 2: Bring down 3 (ones digit). 3 ÷ 3 = 1 one. Write 1 in the ones place.
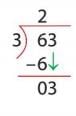
- Multiply: 3 × 1 = 3. Subtract: 3 - 3 = 0.
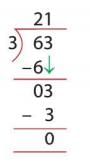
- Quotient is 21 (63 ÷ 3 = 21).
Concept of Remainder
- The remainder is the amount left when the divisor does not divide the dividend completely.
- Steps to find the remainder:
- Perform long division.
- The number left after the final subtraction is the remainder.
Checking Division
- Checking division: Dividend = (Divisor × Quotient) + Remainder.
Example:
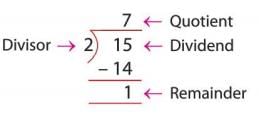
Divide 15 by 2.
- 2 goes into 15 seven times: 2 × 7 = 14.
- Subtract: 15 - 14 = 1 (remainder).
- Quotient is 7, remainder is 1.
- Check: (2 × 7) + 1 = 14 + 1 = 15 (matches dividend).
Division of a Number by a 2-Digit Number
- Used to divide a number by a 2-digit divisor.
- Steps for division by a 2-digit number:
- Take the first two or three digits of the dividend that are divisible by the divisor.
- Find how many times the divisor fits into these digits.
- Multiply, subtract, and bring down the next digit.
- Repeat until all digits are used.
Example:
Divide 336 by 24.
- Step 1: Take 33 (first two digits). 24 × 1 = 24 (less than 33). Write 1 in quotient.
- Subtract: 33 - 24 = 9.
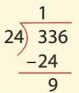
- Step 2: Bring down 6, making 96. 24 × 4 = 96. Write 4 in quotient.
- Subtract: 96 - 96 = 0.
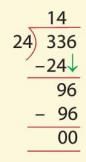
- Quotient is 14 (336 ÷ 24 = 14).
Division of a 3-Digit Number by a 1-Digit Number
- Used to divide a 3-digit number by a 1-digit divisor, resulting in a 2-digit or 3-digit quotient.
- Steps for division:
- Start with the hundreds place. If the digit is less than the divisor, take the first two digits.
- Divide, multiply, subtract, and bring down the next digit.
- Repeat sofisticado all digits are used.
- Check: Dividend = (Divisor × Quotient) + Remainder.
Example:
Divide 115 by 5.
- Step 1: Hundreds digit is 1, less than 5. Take 11 (first two digits). 11 ÷ 5 = 2. Write 2 in quotient.
- Multiply: 5 × 2 = 10. Subtract: 11 - 10 = 1.
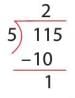
- Step 2: Bring down 5, making 15. 15 ÷ 5 = 3. Write 3 in quotient.
- Multiply: 5 × 3 = 15. Subtract: 15 - 15 = 0.
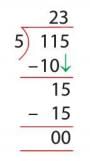
- Quotient is 23 (115 ÷ 5 = 23).
- Check: (5 × 23) + 0 = 115 (matches dividend).
Solving Word Problems
- Word problems involve applying division to real-life situations.
- Steps to solve word problems:
- Identify the total quantity (dividend).
- Identify the number of groups or items per group (divisor).
- Divide to find the quotient.
- Interpret the quotient and remainder (if any) in the context of the problem.
Example:
A school football club has 30 children. They want to form teams with 5 children each. How many teams can they form?
- Total children = 30 (dividend).
- Children per team = 5 (divisor).
- Divide: 30 ÷ 5 = 6.
- 6 teams can be formed.
Framing Word Problems
- Create word problems from a given division statement.
- Steps to frame a word problem:
- Use the dividend as the total quantity.
- Use the divisor as the number of groups or items per group.
- Form a real-life scenario where the quotient is the answer.
Example:
Frame 2 word problems for 156 ÷ 6.
- Problem 1: 156 marbles are to be kept in 6 boxes with an equal number in each. How many marbles per box?
- Solution: 156 ÷ 6 = 26 marbles per box.
- Problem 2: 156 toffees are distributed among children so each gets 6 toffees. How many children get toffees?
- Solution: 156 ÷ 6 = 26 children.
|
98 docs|14 tests
|
FAQs on Division Chapter Notes - Mathematics Class 4 ICSE
| 1. What is division by equal sharing? |  |
| 2. How does division as repeated subtraction work? |  |
| 3. What are division facts and why are they important? |  |
| 4. How do you perform long division? |  |
| 5. What is the concept of remainder in division? |  |
















