Squares and Square Roots Chapter Notes | Mathematics Class 8 ICSE PDF Download
Introduction
The chapter "Squares and Square Roots" introduces the concepts of squaring a number and finding its square root, which are fundamental in mathematics. A square is the result of multiplying a number by itself, while a square root is the number that, when multiplied by itself, gives the original number. This chapter explores how to identify perfect squares, calculate square roots using different methods, and understand the properties of square numbers. It provides a foundation for solving problems involving squares and their roots, with practical applications in various mathematical contexts.

Review
- Square: A number multiplied by itself produces its square.
- Example: 5 × 5 = 25, so 25 is the square of 5, written as 5² = 25.
- Decimal example: 0.2 × 0.2 = 0.04, so 0.04 is the square of 0.2.
- Square Root: The square root of a number x is a number that, when squared, equals x.
- Example: The square root of 36 is 6 because 6² = 36.
- Symbol: The square root is denoted by the radical sign √.
- Examples:
- √64 = 8
- √1.44 = 1.2
- Origin of Symbol: The radical sign √ resembles the letter 'r', from the Latin word "radix" meaning root.
- Power Notation: 4² = 16 is read as "4 raised to the power 2 is 16."
- Even Numbers: Squares of even numbers are always even.
- Examples:
- 2² = 4
- 6² = 36
- 14² = 196
- Odd Numbers: Squares of odd numbers are always odd.
- Examples:
- 3² = 9
- 7² = 49
- 15² = 225
- Positive Squares: The square of any number, positive or negative, is always positive.
- Examples:
- (3)² = 9
- (-3)² = 9
- (-5)² = 25
- (8)² = 64
- Square Root Limitation: Square roots of positive numbers exist, but square roots of negative numbers are not possible in real numbers.
Perfect Square
Definition: A perfect square is a number whose square root is a whole number or a simple fraction.
Examples:
- 16 (√16 = 4)
- 49 (√49 = 7)
- 1.21 (√1.21 = 1.1)
- 9/16 (√(9/16) = 3/4)
Identifying Perfect Squares
- Step 1: Break the number into its prime factors.
- Step 2: Check if all prime factors can be grouped into pairs where both factors in each pair are equal.
- Step 3: If all factors form pairs, the number is a perfect square.
Example 1: For 196:
- Factorize: 196 = 2 × 2 × 7 × 7.
- Pairs: (2 × 2) and (7 × 7).
- Conclusion: Since all factors are paired, 196 is a perfect square.
Example 2: For 180:
- Factorize: 180 = 2 × 2 × 3 × 3 × 5.
- Pairs: (2 × 2) and (3 × 3), but 5 is unpaired.
- Conclusion: Since one factor (5) is unpaired, 180 is not a perfect square.
To Find the Square Root of a Perfect Square Number (Using Prime Factor Method)
Steps to Find Square Root
- Step 1: Factorize the number into its prime factors.
- Step 2: Group the prime factors into pairs where both factors in each pair are equal.
- Step 3: Take one factor from each pair.
- Step 4: Multiply these factors to get the square root.
Example: Find √484:
- Factorize: 484 = 2 × 2 × 11 × 11.
- Pairs: (2 × 2) and (11 × 11).
- Take one factor: 2 × 11.
- Multiply: 2 × 11 = 22.
- Result: √484 = 22.
Making a Perfect Square (Multiplication)
- Step 1: Factorize the number.
- Step 2: Identify unpaired prime factors.
- Step 3: Multiply the number by the unpaired factors to form pairs.
Example: For 980 = 2 × 2 × 5 × 7 × 7, factor 5 is unpaired. Multiply by 5 to get 980 × 5 = 2 × 2 × 5 × 5 × 7 × 7, a perfect square. Square root = 2 × 5 × 7 = 70.
Making a Perfect Square (Division)
- Step 1: Factorize the number.
- Step 2: Identify unpaired prime factors.
- Step 3: Divide the number by the product of unpaired factors.
Example: For 3150 = 2 × 5 × 5 × 3 × 3 × 7, factors 2 and 7 are unpaired. Divide by 2 × 7 = 14 to get 3150 ÷ 14 = 5 × 5 × 3 × 3, a perfect square.
Square Root of Fractions
Rule: Square root of a fraction = (Square root of numerator) ÷ (Square root of denominator).
Examples:
- Example: For 2 7/9 = 25/9, √(25/9) = √25 ÷ √9 = 5/3 = 1 2/3.
- Example: For 4.41 = 441/100, √(441/100) = √441 ÷ √100 = (3 × 7) ÷ (2 × 5) = 21/10 = 2.1.
Alternative Method (Index Form)
- Write prime factors in index form (e.g., 2⁴ × 7²).
- Take half of each index to find the square root.
Example: √784 = √(2⁴ × 7²) = 2² × 7¹ = 4 × 7 = 28.
Note:
Decimals:
- √9 = 3, but √0.9 ≠ 0.3 because (0.3)² = 0.09, so √0.09 = 0.3.
- √144 = 12, but √14.4 ≠ 1.2 because (1.2)² = 1.44, so √1.44 = 1.2.
Square Root Parity:
- Square root of a perfect square even number is even (e.g., √16 = 4, √36 = 6).
- Square root of a perfect square odd number is odd (e.g., √9 = 3, √25 = 5).
To Find the Square Root of a Perfect Square Number (Using Division Method)
Division Method Steps
- Step 1: Group the digits of the number in pairs from the right (for decimals, pair digits before and after the decimal point).
- Step 2: Find the largest number whose square is less than or equal to the first pair or single digit. Write it as the first digit of the quotient and subtract its square from the first pair.
- Step 3: Bring down the next pair of digits. Double the current quotient and write it on the left.
- Step 4: Find the largest digit to add to the doubled quotient such that the product of the new number and this digit is less than or equal to the current remainder plus the new pair. Write this digit in the quotient.
- Step 5: Subtract the product from the current number and bring down the next pair. Repeat until all pairs are processed.
Example: Find √276676:
- Pair digits: 27 | 66 | 76.
- First pair (27): Largest square ≤ 27 is 5² = 25. Quotient = 5, subtract 25, remainder = 2.
- Bring down 66 to get 266. Double quotient (5 × 2 = 10). Find digit x such that (10x) × x ≤ 266. Try x = 2: 102 × 2 = 204. Subtract 204 from 266, remainder = 62.
- Bring down 76 to get 6276. Double quotient (52 × 2 = 104). Find x such that (104x) × x ≤ 6276. Try x = 6: 1046 × 6 = 6276. Subtract, remainder = 0.

- Result: √276676 = 526.
To Find the Square Root of a Number Which is Not a Perfect Square (Using Division Method)
Decimal Precision
- To find the square root correct to n decimal places, calculate up to n+1 decimal places and round off.
- Example: For 2 decimal places, compute to 3 decimal places, then round.
Preparing the Number
- Add zeros after the decimal point to form pairs (e.g., for 3 decimal places, ensure 3 pairs after the decimal).
- Example 1: 24.729 = 24.72 | 90 | 00.
- Example 2: Find √24.729 to 2 decimal places:
- Pair: 24 | 72 | 90 | 00.
- First pair (24): 4² = 16. Quotient = 4, remainder = 8.
- Bring down 72 to get 872. Double 4 = 8. Try 89 × 9 = 801 ≤ 872. Subtract, remainder = 71.
- Bring down 90 to get 7190. Double 49 = 98. Try 987 × 7 = 6909 ≤ 7190. Subtract, remainder = 281.
- Bring down 00 to get 28100. Double 497 = 994. Try 9942 × 2 = 19884 ≤ 28100. Subtract, remainder = 8216.
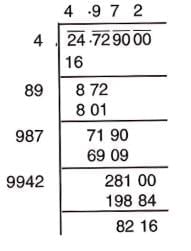
- Result: √24.729 ≈ 4.972 (to 3 decimals) ≈ 4.97 (to 2 decimals).
Making a Perfect Square (Subtraction)
- Find the square root of the number using the division method until the remainder is less than the next possible square.
- Subtract the remainder to get a perfect square.
- Example: For 2433, √2433 ≈ 49 (since 49² = 2401). Remainder = 2433 - 2401 = 32. Subtract 32 to get 2401, a perfect square (√2401 = 49).
Making a Perfect Square (Addition)
- Find the square root until the remainder appears. Take the next integer’s square and subtract the original number.
- Example: For 18265, √18265 ≈ 135 (135² = 18225). Next square is 136² = 18496. Add 18496 - 18265 = 231 to get a perfect square.
Properties of Square Numbers
1st Property
- The unit’s digit of a square number is 0, 1, 4, 5, 6, or 9.
- Examples:
- 11² = 121 (ends in 1)
- 22² = 484 (ends in 4)
- 30² = 900 (ends in 0)
- 25² = 625 (ends in 5)
2nd Property
- Numbers ending in 2, 3, 7, or 8 are never perfect squares.
- Examples: 12, 23, 37, 48 are not perfect squares.
3rd Property
- If a number ends in 1 or 9, its square ends in 1.
- Examples:
- 1² = 1
- 11² = 121
- 9² = 81
- 29² = 841
4th Property
- If a number ends in 4 or 6, its square ends in 6.
- Examples:
- 4² = 16
- 6² = 36
- 24² = 576
- 36² = 1296
5th Property
- If a number ends with n zeros, its square ends with 2n zeros.
- Examples:
- 30² = 900 (2 zeros)
- 300² = 90000 (4 zeros)
Note: A number with an odd number of zeros cannot be a perfect square (e.g., 40, 360, 49000).
6th Property
- A perfect square divided by 3 leaves a remainder of 0 or 1.
- Examples:
- 9 ÷ 3 = 3 (remainder 0)
- 16 ÷ 3 = 5 remainder 1
7th Property
- For any natural number n, (n+1)² - n² = n + (n+1).
- Examples:
- 8² - 7² = 8 + 7 = 15
- 15² - 14² = 15 + 14 = 29
Decimal Squares
- The square of a decimal number has an even number of decimal places, double the number in the square root.
- Examples:
- (0.7)² = 0.49 (2 decimal places)
- (0.03)² = 0.0009 (4 decimal places)
- √0.49 = 0.7
- √0.0009 = 0.03
Note: A decimal number is a perfect square only if it has an even number of decimal places.
|
23 videos|98 docs|14 tests
|
FAQs on Squares and Square Roots Chapter Notes - Mathematics Class 8 ICSE
| 1. What is a perfect square number? |  |
| 2. How do you find the square root of a perfect square using the prime factor method? |  |
| 3. What is the division method for finding the square root of a perfect square? |  |
| 4. Can you find the square root of a number that is not a perfect square using the division method? |  |
| 5. What are the properties of square numbers? |  |
















