Algebraic Expressions Chapter Notes | Mathematics Class 8 ICSE PDF Download
| Table of contents |

|
| Introduction |

|
| Review |

|
| Algebraic Expressions |

|
| Degree of a Polynomial |

|
| Product, Factor, and Coefficient |

|
| Like and Unlike Terms |

|
| Combining Like Terms |

|
| Multiplication |

|
| Division |

|
| Simplification |

|
Introduction
The chapter on Algebraic Expressions introduces students to the fundamental concepts of algebra, which is a branch of mathematics dealing with symbols and the rules for manipulating these symbols. In this chapter, we explore how constants and variables combine to form terms and expressions, and how operations like addition, subtraction, multiplication, and division are performed on these expressions. Understanding these concepts is essential as they form the foundation for solving equations and tackling more advanced mathematical problems. The chapter covers key ideas such as identifying terms, classifying expressions, determining the degree of polynomials, and performing operations while following specific rules like BODMAS.
Review
Constant: A symbol with a fixed value.
- Example: Numbers like 8, 23, 7¾, -15, √3, 2+√5 are constants.
Variable: A symbol that can take different values as needed.
- Example: Letters like x, y, z, p, q are variables.
Combination of Constants and Variables:
- A combination of a constant and a variable is considered a variable.
- Example: 5x, 5 + x, 5 ÷ x, x ÷ 5, x - 5, 5 - x, 8x are variables.
- A combination of two or more variables is also a variable.
- Example: xy, x/y, y/x, x - y, y - x, x + y, xyz, xy/z, xy/yz are variables.
- Other combinations like 15 + x - y, 15x - y, 15 - xy, 15x/y, 15/xy, 15xy are also variables.
Term
- A single number, variable, or a product/quotient of numbers and variables.
- Example: 7, x, 5x, 3xy, -6, 18/xy, yz/x are terms.
- Representation of Terms: Terms are written as products of their factors.
- Example: 7x = 7 × x, xy = x × y, 3xy = 3 × x × y, 5xyz = 5 × x × y × z, 4xy/pq = (4 × x × y)/(p × q).
Algebraic Expressions
- Definition: An algebraic expression is a single term or a combination of terms connected by plus (+) or minus (-) signs.
- Example: 5 - y, 3x² - 5x, 6xy + z, 8 + x² - 3x, 8x + 5y - 7z, xy - 6z + 4 are algebraic expressions.
Terms in an Expression
- Parts of an expression separated by + or - signs are called terms.
- Examples:
- In 5x³ - 8xy + 7y², the terms are 5x³, -8xy, and 7y².
- In 4xy² + 8xy - 7y² + 5, the terms are 4xy², 8xy, -7y², and +5.
- 3x² × 8y is one term, and 3x² ÷ 8y is also one term.
Note: Multiplication (×) and division (÷) signs do not separate terms.
Types of Algebraic Expressions
- Monomial:An expression with only one term.
- Example: 3, 6/11, x, 7x, 8xy, 9x²/y, yz/x, 5x²y/z, 6y/xz² are monomials.
- Binomial:An expression with exactly two different terms.
- Example: 8 + x, xy - 4, 4x/y - 8y, 4x² + 6xy, yz²+zx are binomials.
- Trinomial:An expression with exactly three different terms.
- Example: 3 + x + y, 7x + 11 - y², ax² + bx + c, xy + yz - zx are trinomials.
- Polynomial:An expression with two or more different terms.
- Example: x² - 5x, x - 3xy + y², 1 - 5y + xy + x²y are polynomials.
Note: Expressions like (x² + xy + y²)/(x - 3y), (x² + a²)/(x + a), x/2y, (3x - y)/(8ax) are not polynomials.
Degree of a Polynomial
Single Variable Polynomial
- The degree is the highest power of the variable in the polynomial.
- Steps:
- Identify the term with the highest power of the variable.
- The exponent of that term is the degree.
- Examples:
- In 3x² - 8x + 4, the term 3x² has the highest power (2), so the degree is 2.
- In 4x - 7x⁵ + 8, the degree is 5 (from 7x⁵).
- In (3/7)y² + (4/9)y⁵ - (1/5)y⁸+15y, the degree is 8 (from y⁸).
- In 8 - 5x, the degree is 1 (from 5x).
Polynomial with Multiple Variables
- The degree is the highest sum of the powers of variables in any term.
- Steps:
- Calculate the sum of the powers of variables in each term.
- The highest sum is the degree of the polynomial.
- Examples:
- In 7x³y⁴-8x²y³z⁴+5x⁴y³z:
- Term 7x³y⁴: 3+4=7
- Term -8x²y³z⁴: 2+3+4=9
- Term 5x⁴y³z: 4+3+1=8
- Degree is 9 (highest sum).
- In 5x²y-4x³y⁵+6, the degree is 8 (from 4x³y⁵: 3+5=8).
- In xy²z³+4x³y³z⁴-5x²yz³, the degree is 10 (from 4x³y³z⁴: 3+3+4=10).
Types of Polynomials by Degree
- Linear Polynomial: Degree is 1.
- Quadratic Polynomial: Degree is 2.
- Cubic Polynomial: Degree is 3.
Note: A polynomial’s terms must have non-negative integer degrees.
Product, Factor, and Coefficient
Product
- The result of multiplying two or more numbers, variables, or both.
- Examples:
- 3abc is the product of 3, a, b, and c.
- 5x²yz is the product of 5, x², y, and z (or 5, x, x, y, z).
Factor
- Each quantity (constant or variable) that forms a product.
- Example: In 5x, the factors are 5 and x.
Types of Factors
- Numeral Factor: The constant part of a term.
- Example: In 5x, 5 is the numeral factor.
- Literal Factor: The variable part of a term.
- Examples:
- In 5x, x is the literal factor.
- In 5x²y, the numeral factor is 5, and the literal factors are x, y, x², xy, x²y.
- 5x is divisible by both 5 and x.
- Examples:
Coefficient:
Any factor of a term is a coefficient of the remaining part.
- Example: In 7xyz:
- 7 is the coefficient of xyz.
- 7x is the coefficient of yz.
- 7xy is the coefficient of z.
- xz is the coefficient of 7y.
Note: Each factor completely divides the term.
Like and Unlike Terms
Like Terms
- Terms with the same literal coefficients (same variables with same powers).
- Examples:
- 6xy², -8xy², 15xy², 23xy², -5/7xy² are like terms (all have xy²).
- 5xyz, 8xyz, -6xyz, 2/3xyz are like terms (all have xyz).
Unlike Terms
- Terms with different literal coefficients.
- Examples:
- x²y and xy² are unlike terms.
- 7xy²z, 8x²yz, -15xyz² are unlike terms.
Combining Like Terms
- Definition: Adding or subtracting like terms by combining their numerical coefficients and keeping the common literal factor.
- Steps:
- Identify like terms.
- Add or subtract their numerical coefficients.
- Place the result before the common literal factor.
- Examples:
- 3x + 2x = (3+2)x = 5x.
- 4x² + 15x² = (4+15)x² = 19x².
- 8xy - 5xy = (8-5)xy = 3xy.
- 9xy² - 15xy² + 11xy² = (9 - 15 + 11)xy² = 5xy².
- Combining Polynomials: Combine like terms of the given polynomials.
Note: Unlike terms cannot be combined into a single term.
Multiplication
Multiplying Literals
- When multiplying powers of the same variable, add the exponents.
- Examples:
- xm × xn = x(m+n).
- x³ × x⁵ = x(3+5) = x⁸.
- x²y³ × x³y⁵ = x(2+3)y(3+5) = x⁵y⁸.
- x⁴y²z³ × x³yz² × x²y²z = x(4+3+2)y(2+1+2)z(3+2+1) = x⁹y⁵z⁶.
Multiplying a Monomial by a Monomial
- Multiply the numerical coefficients and the literal coefficients separately, then combine.
- Steps:
- Multiply the numerical coefficients.
- Multiply the literal coefficients by adding exponents of like variables.
- Combine the results.
- Examples:
- (6a²b³) × (-4a³b⁴) = (6 × -4)(a²⁺³b³⁺⁴) = -24a⁵b⁷.
- (4x²y⁵z) × (-5xy³z²) × (2x³yz⁴) = (4 × -5 × 2)(x²⁺¹⁺³y⁵⁺³⁺¹z¹⁺²⁺⁴) = -40x⁶y⁹z⁷.
Multiplying a Polynomial by a Monomial
- Multiply each term of the polynomial by the monomial.
- Steps:
- Multiply the monomial by each term of the polynomial.
- Simplify each resulting term.
- Example:
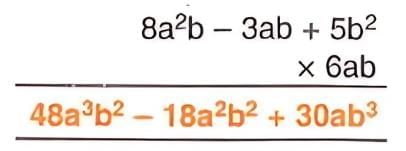
Multiplying a Polynomial by a Polynomial
- Multiply each term of one polynomial by each term of the other, then combine like terms.
- Steps:
- Multiply each term of the first polynomial by each term of the second polynomial.
- Combine like terms in the result.
- Example:
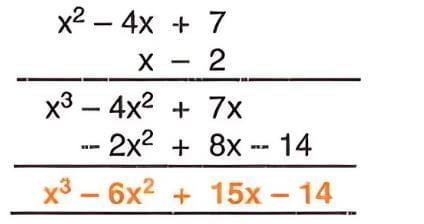
Division
Dividing Literals
- When dividing powers of the same variable, subtract the exponents.
- Examples:
- xm ÷ xn = x(m-n) if m > n; or 1/x(n-m) if n > m.
- x⁷ ÷ x⁵ = x(7-5) = x².
- x⁵ ÷ x⁷ = 1/x(7-5) = 1/x².
- (x⁸y⁴)/(x³y²) = x(8-3)y(4-2) = x⁵y².
- (x⁵y²z⁷)/(x²y⁶z³) = x(5-2)y(2-6)z(7-3) = x³z⁴/y⁴.
- (18y⁸z³)/(3y⁴z⁵) = (18/3)y(8-4)z(3-5) = 6y⁴/z².
Dividing a Monomial by a Monomial
- Divide the numerical coefficients and the literal coefficients separately, then combine.
- Steps:
- Divide the numerical coefficients.
- Divide the literal coefficients by subtracting exponents of like variables.
- Combine the results.
- Examples:
- (36a⁷) ÷ (-12a³) = (36/-12)(a⁷/a³) = -3a⁴.
- (-50a²b³) ÷ (-15a⁴b²) = (-50/-15)(a²/a⁴)(b³/b²) = (10/3)(b/a²) = 10b/3a².
Dividing a Polynomial by a Monomial
- Divide each term of the polynomial by the monomial and simplify.
- Steps:
- Divide each term of the polynomial by the monomial.
- Simplify each resulting term.
- Examples:
- (9a⁵ - 6a²) ÷ 3a² = (9a⁵/3a²) - (6a²/3a²) = 3a³ - 2.
- (8x²y - 6xy + 5xy²) ÷ 2xy = (8x²y/2xy) - (6xy/2xy) + (5xy²/2xy) = 4x - 3 + (5/2)y.
Dividing a Polynomial by a Polynomial
- Use polynomial long division to find the quotient and remainder.
- Steps:
- Arrange the dividend and divisor in ascending or descending order of their literal coefficients.
- Divide the first term of the dividend by the first term of the divisor to get the first term of the quotient.
- Multiply the divisor by this quotient term and subtract from the dividend.
- Use the remainder as the new dividend and repeat until the degree of the remainder is less than the degree of the divisor.
- Example: Divide 8x² + 18xy - 45y² by 2x - 3y:
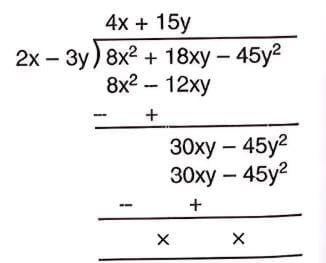
- First term: (8x²)/(2x) = 4x.
- Multiply: 4x(2x - 3y) = 8x² - 12xy.
- Subtract: (8x² + 18xy - 45y²) - (8x² - 12xy) = 30xy - 45y².
- Next term: (30xy)/(2x) = 15y.
- Multiply: 15y(2x - 3y) = 30xy - 45y².
- Subtract: (30xy - 45y²) - (30xy - 45y²) = 0.
- Quotient = 4x + 15y, Remainder = 0.
- First term: (8x²)/(2x) = 4x.
Simplification
Using Brackets
- Brackets indicate operations to be performed in a specific order.
Types of Brackets
- Vinculum or bar brackets: ¯
- Parenthesis or small brackets: ( )
- Curly brackets or middle brackets: { }
- Square brackets or big brackets: [ ]
Order of Removal
Remove brackets in the order: vinculum, parenthesis, curly, square.
Example: Simplify 84 - 7[-11x - 4[-17x + 3(8 - 9 - 5x)]]:
- Inner parenthesis: 8 - 9 - 5x = 5x - 1.
- Multiply: 3(5x - 1) = 15x - 3.
- Inside square brackets: -17x + (15x - 3) = -2x - 3.
- Multiply: -4(-2x - 3) = 8x + 12.
- Inside square brackets: -11x + (8x + 12) = -3x + 12.
- Multiply: -7(-3x + 12) = 21x - 84.
- Finally: 84 + (21x - 84) = 21x.
Principle of BODMAS
- Follow the order of operations: Brackets, Of (multiplication), Division, Multiplication, Addition, Subtraction.
- Steps:
- Remove brackets in the correct order.
- Perform multiplication indicated by "of".
- Perform division.
- Perform multiplication.
- Perform addition.
- Perform subtraction.
- Examples:
- Simplify x⁵ ÷ x⁷ × x⁴:
- Division first: x⁵ ÷ x⁷ = x^(5-7) = 1/x².
- Multiply: (1/x²) × x⁴ = x^(4-2) = x².
- Simplify 5y × [6y ÷ 3 + (4 - (3y - 2y - 4))]:
- Inner parenthesis: 3y - 2y - 4 = y - 4.
- Inside parenthesis: 4 - (y - 4) = 4 - y + 4 = -y + 8.
- Division: 6y ÷ 3 = 2y.
- Inside square brackets: 2y + (-y + 8) = y + 8.
- Multiply: 5y × (y + 8) = 5y² + 40y.
|
23 videos|98 docs|14 tests
|
FAQs on Algebraic Expressions Chapter Notes - Mathematics Class 8 ICSE
| 1. What is an algebraic expression? |  |
| 2. How do you determine the degree of a polynomial? |  |
| 3. What is the difference between like and unlike terms? |  |
| 4. How can you combine like terms in an expression? |  |
| 5. What are the steps to simplify an algebraic expression? |  |














