Factors and Multiples Chapter Notes | Mathematics Class 4 ICSE PDF Download
Introduction
Ever wondered how numbers connect with each other like pieces of a puzzle? The chapter "Factors and Multiples" is like a treasure map that helps us explore the fascinating world of numbers! By understanding factors and multiples, we can unlock secrets about how numbers divide, multiply, and share special relationships. From finding what numbers can evenly divide another to discovering numbers that are multiples of others, this chapter is packed with fun and useful math tricks. Get ready to dive into prime and composite numbers, learn cool methods like factor trees, and master divisibility rules that make math feel like a game!

Factors of a Number
- Factors are numbers that multiply together to give a specific number. A factor divides a number completely without leaving any remainder. Factors can be found using multiplication or division methods.
Steps to find factors by multiplication:
- Identify pairs of numbers that multiply to give the target number.
- List all unique numbers from these pairs as factors.
Steps to find factors by division:
- Divide the number by divisors that result in a remainder of 0.
- Both the divisor and quotient are factors.
- Stop when divisors start repeating or are not possible.
Example: Find all factors of 24.
By multiplication:
- 1 × 24 = 24 (factors: 1, 24)
- 2 × 12 = 24 (factors: 2, 12)
- 3 × 8 = 24 (factors: 3, 8)
- 4 × 6 = 24 (factors: 4, 6)
Factors of 24 are 1, 2, 3, 4, 6, 8, 12, 24.
By division:
- 24 ÷ 1 = 24 (remainder 0, factors: 1, 24)
- 24 ÷ 2 = 12 (remainder 0, factors: 2, 12)
- 24 ÷ 3 = 8 (remainder 0, factors: 3, 8)
- 24 ÷ 4 = 6 (remainder 0, factors: 4, 6)
Factors of 24 are 1, 2, 3, 4, 6, 8, 12, 24.
Properties of Factors
- 1 is the smallest factor of every number.
- 1 is the only number with exactly one factor (itself).
- Every number is a factor of itself and is its greatest factor.
- Every number has a limited number of factors.
- Factors are always less than or equal to the number.
Example: Find the factors of 12.
1 × 12 = 12
2 × 6 = 12
3 × 4 = 12
Factors of 12 are 1, 2, 3, 4, 6, 12.
Here, 1 is the smallest factor, 12 is the greatest, and there are only 6 factors.
Common Factors
Common factors are numbers that are factors of two or more numbers.
Steps to find common factors:
- List the factors of each number.
- Identify the numbers that appear in all factor lists.
Example: Find the common factors of 6 and 18.
Factors of 6: 1, 2, 3, 6
Factors of 18: 1, 2, 3, 6, 9, 18
Common factors: 1, 2, 3, 6
Multiples of a Number
Multiples are the results of multiplying a number by counting numbers (1, 2, 3, ...).
Steps to find multiples:
- Multiply the number by 1, 2, 3, and so on.
- List the products as multiples.
- To check if a number is a multiple of another, divide the larger number by the smaller one.
- If the remainder is 0, it’s a multiple.
Example: Find the first five multiples of 8.
8 × 1 = 8
8 × 2 = 16
8 × 3 = 24
8 × 4 = 32
8 × 5 = 40
First five multiples of 8 are 8, 16, 24, 32, 40.
Properties of Multiples
- Every number is a multiple of 1.
- Every number is a multiple of itself.
- The smallest multiple of a number is the number itself.
- A number has infinitely many multiples.
- Every multiple is exactly divisible by the original number.
- Multiples are greater than or equal to the original number.
Example: Check if 264 is a multiple of 2.
Divide 264 ÷ 2 = 132 (remainder 0)
Since the remainder is 0, 264 is a multiple of 2.
Common Multiples
Common multiples are numbers that are multiples of two or more numbers.
Steps to find common multiples:
- List the multiples of each number.
- Continue until at least two common multiples are found.
- The smallest common multiple is called the Least Common Multiple (LCM).
Example: Find two common multiples of 2, 3, and 4.
Multiples of 2: 2, 4, 6, 8, 10, 12, 14, 16, 18, 20, 22, 24, ...
Multiples of 3: 3, 6, 9, 12, 15, 18, 21, 24, ...
Multiples of 4: 4, 8, 12, 16, 20, 24, ...
Common multiples: 12, 24
Even and Odd Numbers
- Even numbers are multiples of 2 and end in 0, 2, 4, 6, or 8.
- Odd numbers are not divisible by 2 and end in 1, 3, 5, 7, or 9.
- 2 is a factor of all even numbers.
Example: Numbers like 2, 4, 6, 8, 10 are even (divisible by 2). Numbers like 1, 3, 5, 7, 9 are odd (not divisible by 2).
Prime and Composite Numbers
- Prime numbers have only two factors: 1 and themselves.
- Composite numbers have more than two factors.
- 2 is the smallest and only even prime number.
- 0 and 1 are neither prime nor composite.
- Co-prime numbers have only 1 as their common factor.
- Steps to identify prime or composite numbers:
- List all factors of the number.
- If it has only two factors, it’s prime.
- If it has more than two factors, it’s composite.
Prime and Composite Numbers between 1 and 100
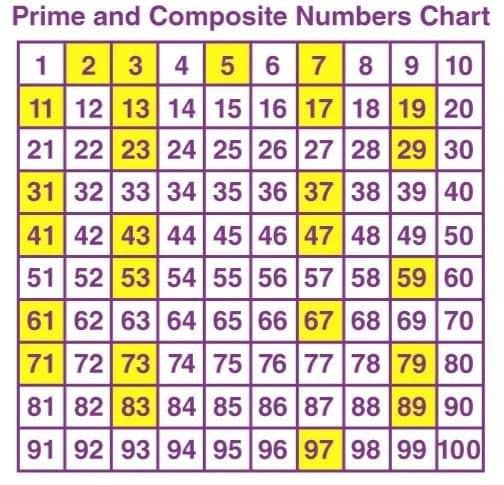
Example: Check if 7, 19, 27, and 35 are prime or composite.
Factors of 7: 1, 7 (prime, only two factors)
Factors of 19: 1, 19 (prime, only two factors)
Factors of 27: 1, 3, 9, 27 (composite, more than two factors)
Factors of 35: 1, 5, 7, 35 (composite, more than two factors)
Prime Factors
- Prime factors are prime numbers that divide a number exactly.
- Every composite number can be expressed as a product of prime factors.
- Two methods to find prime factors: Factor Tree Method and Prime Factorization Method.
Example: Write 24 as a product of prime factors.
24 = 2 × 12
12 = 2 × 6
6 = 2 × 3
So, 24 = 2 × 2 × 2 × 3 (all prime numbers).
Factor Tree Method
Break down a number into factors until all factors are prime.
Steps:
- Start with the number and divide it into two factors.
- Continue dividing each factor until only prime numbers remain.
- Circle the prime numbers and write them as the product.
Example: Find prime factors of 96 using a factor tree.
Prime factors: 2, 2, 2, 2, 2, 3 (so, 96 = 2 × 2 × 2 × 2 × 2 × 3).
Prime Factorization Method
Divide the number by the smallest prime number possible until the quotient is 1.
Steps:
- Start with the smallest prime number that divides the number exactly.
- Divide repeatedly, updating the quotient each time.
- Multiply all prime divisors to get the prime factors.
Example: Find prime factors of 84 using prime factorization.
84 ÷ 2 = 42
42 ÷ 2 = 21
21 ÷ 3 = 7
7 ÷ 7 = 1
Prime factors: 2 × 2 × 3 × 7.
Tests of Divisibility
- Divisibility rules help determine if a number is divisible by another without performing division.
- Divisibility by 2: The ones digit is 0, 2, 4, 6, or 8.
- Divisibility by 3: The sum of all digits is divisible by 3.
- Divisibility by 4: The number formed by the last two digits is divisible by 4.
- Divisibility by 5: The ones digit is 0 or 5.
- Divisibility by 9: The sum of all digits is divisible by 9.
- Divisibility by 10: The ones digit is 0.
Example: Check if 342 is divisible by 3.
Sum of digits: 3 + 4 + 2 = 9
9 is divisible by 3, so 342 is divisible by 3.
Highest Common Factor (H.C.F.)
- H.C.F. is the greatest number that divides all given numbers without a remainder.
- Also called the Greatest Common Factor (G.C.F.).
- Found using the Listing Method or Common Division Method.
Example: Find the H.C.F. of 12 and 18 by listing method.
Factors of 12: 1, 2, 3, 4, 6, 12
Factors of 18: 1, 2, 3, 6, 9, 18
Common factors: 1, 2, 3, 6
- H.C.F. is 6.
Listing Method
Steps:
- List all factors of each number.
- Identify common factors.
- Choose the highest common factor as the H.C.F.
Example: Find the H.C.F. of 12 and 18 by listing method.
Factors of 12: 1, 2, 3, 4, 6, 12
Factors of 18: 1, 2, 3, 6, 9, 18
Common factors: 1, 2, 3, 6
H.C.F. is 6.
Common Division Method or Prime Factorization Method
Steps:
- Write the numbers in a row, separated by commas.
- Divide by the smallest common prime factor.
- Continue dividing the quotients until no common factors remain.
- Multiply the common prime factors to get the H.C.F.
Example: Find the H.C.F. of 15 and 30 using common division method.
Divide 15, 30 by 3: quotients 5, 10
Divide 5, 10 by 5: quotients 1, 2
No common factors for 1, 2
H.C.F. = 3 × 5 = 15.
Least Common Multiple (L.C.M.)
L.C.M. is the smallest number that is a multiple of all given numbers.
Facts about L.C.M.:
- The product of two prime numbers is their L.C.M.
- If a smaller number is a factor of a larger number, the larger number is the L.C.M.
- Found using the Listing Method or Common Division Method.
Example: Find the L.C.M. of 8 and 24.
Multiples of 8: 8, 16, 24, 32, 40, ...
Multiples of 24: 24, 48, 72, 96, ...
L.C.M. is 24 (since 8 is a factor of 24).
Listing Method
Steps:
- List multiples of each number.
- Identify the smallest number common to all lists.
Example: Find the L.C.M. of 4 and 8 by listing method.
Multiples of 4: 4, 8, 12, 16, 20, ...
Multiples of 8: 8, 16, 24, 32, 40, ...
Common multiples: 8, 16
L.C.M. is 8.
Common Division Method or Prime Factorization Method
Steps:
- Write the numbers in a row, separated by commas.
- Divide by the smallest prime number that divides at least one number.
- Bring down undivided numbers as is.
- Continue until all numbers are reduced to 1.
- Multiply all prime divisors to get the L.C.M.
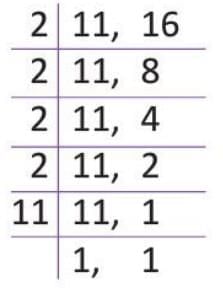
Example: Find the L.C.M. of 11 and 16 by prime factorization method.
- Write the numbers in a row, separated by commas.
- Divide by the smallest prime number that divides at least one number.
- Bring down undivided numbers as is.
- Continue until all numbers are reduced to 1.
- Multiply all prime divisors to get the L.C.M.
- L.C.M. = 2 × 2 × 2 × 2 × 11 = 176.
|
98 docs|14 tests
|
FAQs on Factors and Multiples Chapter Notes - Mathematics Class 4 ICSE
| 1. What are factors of a number? |  |
| 2. How do you find common factors of two numbers? |  |
| 3. What are multiples of a number? |  |
| 4. What is the difference between prime and composite numbers? |  |
| 5. How do you determine if a number is even or odd? |  |