Class 7 Exam > Class 7 Notes > Physics Class 7 ICSE > Chapter Notes: Physical Quantities and Measurement
Physical Quantities and Measurement Chapter Notes | Physics Class 7 ICSE PDF Download
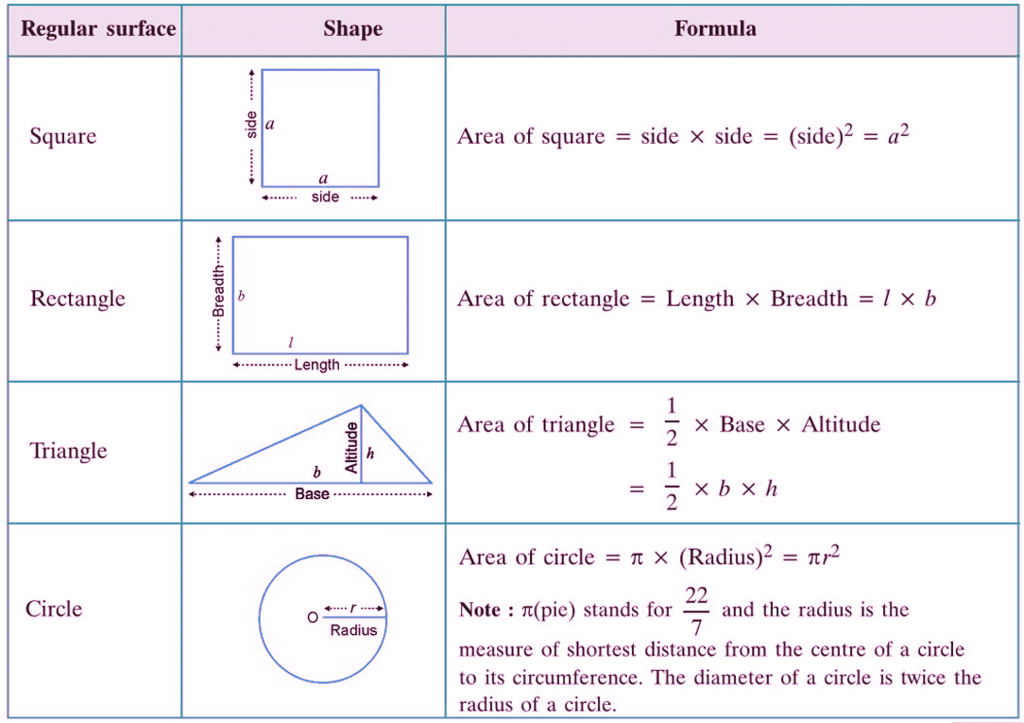
Area and Its Measurement
Measurement of Area
- Area is the amount of surface an object or a place covers.
- We learned how to measure the area of regular surfaces in Class VI.
- We know that the area of a door is bigger than the area of a window.
- The area of a table is larger than the area of a chair.
- We need to measure the area to check how much space an object takes.
- Before measuring area, we need to understand what the term "area" means.
Units of Area
- We need to measure the area of objects like a table or chair.
- We must use standard units to measure area.
- Using non-standard units can give wrong results. For example, if you say the area of your table is equal to the area of four physics books, it might not be correct because different books have different sizes.
- In the Standard International System (SI), the unit of area is the square metre, written as m².
How Big One Square Metre Is
- A square metre (m²) is the area of a square where each side is 1 metre long.
- So, the area of this square is 1 m × 1 m = 1 m².
- A square with sides AB = BC = CD = DA = 1 m has an area of 1 m².
Sub-multiples of Standard Unit of Area
- A square metre is not always easy to use for small objects like a book or a coin.
- For small objects, we use smaller units like square millimetre, square centimetre, or square decimetre.
- 1 m² = 1 m × 1 m.
- 1 m² = 100 cm × 100 cm = 10,000 cm².
- Or, 1 m² = 1,000,000 mm².
- 1 cm² = (1/100) m × (1/100) m = (1/10,000) m².
- So, 1 cm² = 10⁻⁴ m².
- 1 mm² = 10⁻⁶ m².
- 1 dm² = 10⁻² m².
Multiples of Standard Unit of Area
- For large areas like a city or a plot of land, we use bigger units like "are" or "hectare".
- One "are" is the area of a square with each side equal to 10 m.
- 1 are = 10 m × 10 m = 100 m².
- Or, 1 m² = (1/100) are = 10⁻² are.
- 1 hectare = 100 are = 100 × 100 m² = 10,000 m².
- Or, 1 m² = 10⁻⁴ hectare.
- For even bigger areas like a district or a country, we use square kilometre (km²).
- One square kilometre (km²) is the area of a square with each side equal to 1 km.
- 1 km² = 1,000 m × 1,000 m = 1,000,000 m².
- Or, 1 km² = 100 hectares.
- So, 1 km² = 1,000,000 m² = 100 hectares = 10⁶ m².
Formulae for Calculating Areas of Some Regular Surfaces
Measurement of Area of an Irregular Flat Surface
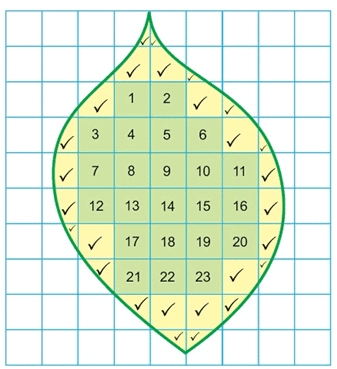
- Sometimes, we need to find the area of irregular objects like a leaf.
- To find the area of an irregular shape, place the object on a centimetre graph paper.
- Use a sharp pencil to draw the outline of the object on the graph paper.
- Count the number of complete squares inside the outline.
- In a diagram, if the number of complete squares is 23, write it down.
- Now, mark the incomplete squares (squares that are not fully inside the outline) with a tick (✓) and count them.
- If the number of incomplete squares is 27, assume the area of each incomplete square is (1/2) of a full square.
- The formula to find the approximate area of the irregular shape (in cm²) is:
- Area = (Number of complete squares) + (Number of incomplete squares × 1/2).
- For example, Area = 23 + (27 × 1/2) = 23 + 13.5 = 36.5 cm².
- This method works well for broad objects like a leaf, but for smaller objects, we use millimetre graph paper.
- On millimetre graph paper, 100 small squares make 1 cm².
Volume and its Measurement
Measurement of volume
We Often State:
- A cylinder is bigger than a test tube.
- A cup is smaller than a bucket.
- A drawing room is bigger than a store room.
- We say these things to compare the space inside objects.
- For example, a bucket can hold more water than a cup because it has more space.
- Similarly, a drawing room has more space than a store room.
- The air inside a store room is less than the air inside a drawing room.
- The space that an object takes up is called its volume.
Units of Volume
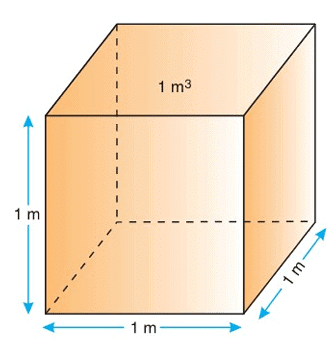
- We measure volume in the Standard International (SI) system using a unit called cubic metre.
- Cubic metre is written as m³.
- One cubic metre (1 m³) is the volume of a cube whose each side is 1 metre long.
- For example, imagine a vessel shaped like a cube where each side (length, breadth, and height) is 1 m.
- The volume of this cube is 1 m³ because 1 m × 1 m × 1 m = 1 m³.
- We use cubic metre to measure the volume of big things like rooms or large containers.
Sub-multiples of Unit of Volume
- For smaller objects, like a matchbox or a glass of water, we use a smaller unit called cubic centimetre.
- Cubic centimetre is written as cm³.
- We also use cubic millimetre (mm³) for even smaller volumes.
Glass Slab (A Regular Body)
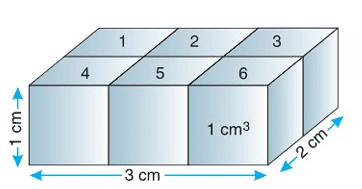
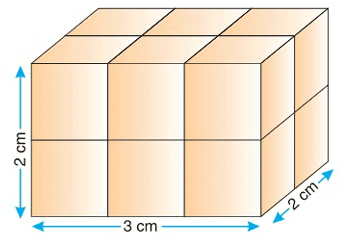
- Suppose we want to find the volume of a rectangular slab.
- The slab has a length of 3 cm, breadth of 2 cm, and height of 2 cm.
- We can find its volume by breaking it into smaller cubes.
- Imagine the slab is made of tiny cubes, each with a side of 1 cm.
- Along the length, there are 3 cubes (since length is 3 cm).
- Along the breadth, there are 2 cubes (since breadth is 2 cm).
- Along the height, there are 2 cubes (since height is 2 cm).
- So, the total number of tiny cubes is 3 × 2 × 2 = 12 cubes.
- Each tiny cube has a volume of 1 cm³ (since 1 cm × 1 cm × 1 cm = 1 cm³).
- So, the total volume of the slab is 12 × 1 cm³ = 12 cm³.
- We can also find the volume directly by using the formula.
- Volume = Length × Breadth × Height.
- For the slab: Volume = 3 cm × 2 cm × 2 cm = 12 cm³.
- This matches our earlier answer!
Note
- One cubic centimetre (1 cm³) is the volume of a cube whose each side is 1 cm.
- So, 1 cm³ = 1 cm × 1 cm × 1 cm.
- 1 m³ = 1 m × 1 m × 1 m.
- 1 m = 100 cm, so 1 m³ = 100 cm × 100 cm × 100 cm = 1,00,00,00 cm³.
Formulae for Calculating the Volume of Regular Bodies
- For a cube: Volume = Length × Length × Length = (Length)³.
- For a cuboid: Volume = Length × Breadth × Height = l × b × h.
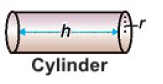
- For a cylinder: Volume = π × (Radius)² × Height = πr²h.
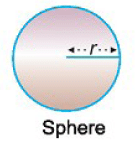
- For a sphere: Volume = (4/3) × π × (Radius)³ = (4/3)πr³.
Measurement of Volume of Liquids
- We measure the volume of liquids using a unit called litre.
- Litre is written as l (small L).
- One litre is also written as 1 L (capital L).
- A smaller unit for liquids is millilitre, written as ml.
- 1 litre (l) = 1000 millilitres (ml).
- 1 millilitre (ml) is the same as 1 cubic centimetre (cm³ or cc).
- So, 1 l = 1000 ml = 1000 cm³.
- Also, 1 m³ = 1,00,00,00 cm³ = 1,00,00,00 ml = 1000 l.
- We measure the volume of liquids using containers that show the capacity, like a measuring cylinder or beaker.
Measuring the Volume of Liquids
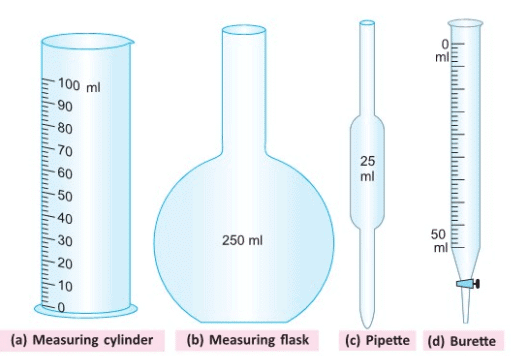
- We use tools like measuring cylinders, measuring flasks, pipettes, and burettes to measure the volume of liquids.
- A measuring cylinder is a tall container with markings to show the volume of liquid inside.
- A measuring flask is a bottle with a narrow neck and markings to measure a specific volume of liquid.
- A pipette is a thin tube used to measure small amounts of liquid accurately.
- A burette is a long tube with a tap at the bottom, used to measure liquids drop by drop.
Reading the Level of Liquid Correctly
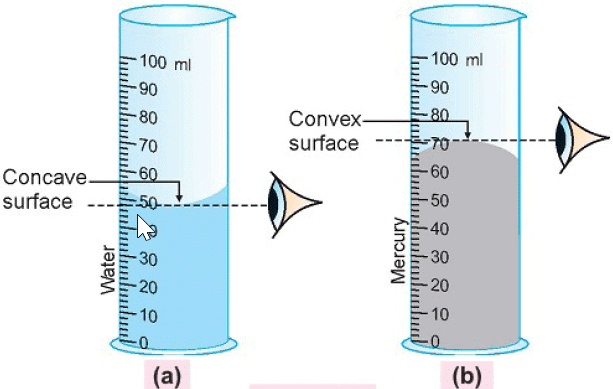
- When we pour a liquid like water or alcohol into a measuring cylinder, the liquid surface is not flat.
- The surface of the liquid curves and forms a shape called a meniscus.
- For liquids like water or alcohol, the meniscus is concave (curves downward).
- We need to read the volume at the lowest point of the concave meniscus.
- We must keep our eye level in line with the lowest point of the meniscus to read the correct volume.
- If we read from above or below the lowest point, we might get the wrong volume.
- Some liquids, like mercury, do not form a concave meniscus.
- For mercury, the meniscus is convex (curves upward).
- For a convex meniscus, we read the volume at the highest point of the curve.
- We must keep our eye level in line with the highest point of the convex meniscus to get the correct volume.
Measurement of Volume of Irregular Solids by Measuring Cylinder
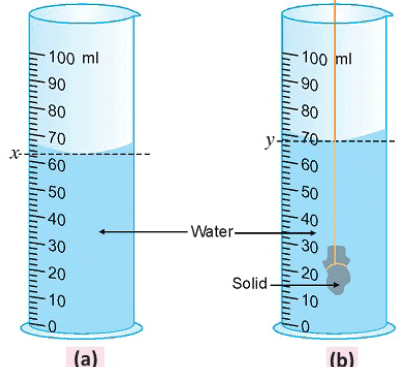
- We can measure the volume of irregular solids, like a stone, using a measuring cylinder.
- First, take a measuring cylinder and fill it with water up to a certain level.
- Keep your eye at the lowest point of the concave meniscus of the water and read the volume.
- Let this volume be x cm³.
- Now, gently tie the solid (like a stone) with a thread and lower it into the water in the measuring cylinder.
- Make sure the solid is completely under the water.
- The water level in the cylinder will rise because the solid takes up space.
- Read the new volume of water by keeping your eye at the lowest point of the meniscus again.
- Let this new volume be y cm³.
- The volume of the solid is the difference between the two volumes.
- Volume of the solid = (y - x) cm³.
To Find Volume of Irregular Solid Using Overflow Jar
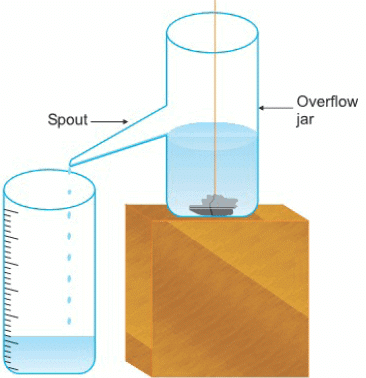
- We can also measure the volume of an irregular solid using an overflow jar.
- An overflow jar is a container with a spout (a small pipe) at the side.
- Fill the overflow jar with water until the water starts to flow out of the spout.
- Wait until the water stops dripping from the spout.
- Place a measuring cylinder under the spout of the overflow jar.
- Gently lower the solid into the overflow jar using a thread.
- The solid will push some water out of the jar through the spout.
- The water that flows out will collect in the measuring cylinder.
- Measure the volume of water in the measuring cylinder by reading the lowest point of the meniscus.
- This volume of water is equal to the volume of the solid.
- If the solid can dissolve in water (like sugar), we should use a liquid in which the solid does not dissolve.
Measurement of Density and Speed
Definition of Density
- Density means how much mass is packed in a certain volume of a substance.
- If an object has more mass in less volume, it has high density.
- For example, if an aluminium cube has a volume of 20 cm³ and weighs 54 g, its density is 54 g ÷ 20 cm³ = 2.7 g/cm³.
- Another aluminium cube with the same volume but a mass of 40 g has a density of 40 g ÷ 20 cm³ = 2 g/cm³.
- The first cube has more density because it has more mass in the same volume.
- The formula for density is: Density = Mass ÷ Volume.
- If M is the mass of an object and V is its volume, then Density = M ÷ V.
- We can also say: Volume = Mass ÷ Density and Mass = Density × Volume.
Units of Density
- In CGS system, mass is measured in grams and volume in cubic centimetres.
- Therefore, the unit of density in CGS system is g/cm3 or gcm-3.
- In SI system, mass is measured in kilograms and volume in cubic metres.
- Therefore, the unit of density in SI system is kg/m3 or kgm-3.
Determination of Density of a Solid by Using a Measuring Cylinder
- We need to find the mass and volume of a solid to calculate its density.
- First, measure the mass of the solid using a physical balance and let it be m grams.
- Take a measuring cylinder and add some water to it. Note the water level, say it is 60 cm³.
- Tie the solid with a thread and gently lower it into the water in the measuring cylinder so it is completely immersed.
- Now, check the new water level. Let it be 100 cm³.
- The volume of the solid is the difference in water levels: Volume = (100 - 60) cm³ = 40 cm³.
- Suppose the mass of the solid is 40 g and its volume is 40 cm³.
- Then, Density = Mass ÷ Volume = 40 g ÷ 40 cm³ = 1 g/cm³.
Determination of Density of a Liquid by Using a Density Bottle
- A density bottle is a small glass bottle with a capacity of 100 ml and a tight-fitting glass stopper with a tiny tube.
- When the bottle is filled with a liquid and the stopper is inserted, the extra liquid comes out through the tube.
- This ensures the bottle always holds the same volume of liquid.
- Here’s how to find the density of a liquid using a density bottle:
- Step 1: Wash the density bottle with distilled water, dry it in hot air, and find its mass using a physical balance. Let it be m g.
- Step 2: Fill the density bottle completely with distilled water, insert the glass stopper, and wipe the bottle dry from the outside. Find its mass again. Let it be m1 g.
- Step 3: Now, pour out the water, dry the bottle in hot air, and fill it with the liquid you want to test (like kerosene, alcohol, or brine solution). Insert the stopper, wipe the bottle dry, and find its mass. Let it be m2 g.
Observations and Calculations
- Mass of empty bottle = m g.
- Mass of empty bottle + water = m1 g.
- Mass of empty bottle + liquid = m2 g.
- Mass of water = (m1 - m) g.
- Mass of liquid = (m2 - m) g.
- Volume of water = (m1 - m) cm3.
- Volume of bottle = (m1 - m) cm3.
- Volume of liquid = Volume of water = (m1 - m) cm3.
- Density of liquid = Mass of liquid ÷ Volume of liquid = (m2 - m) g ÷ (m1 - m) cm3 = (m2 - m)/(m1 - m) g/cm3.
- For example, if the mass of the liquid is 40 g and the volume of the liquid is 50 cm3, then:
- Density of liquid = Mass of liquid ÷ Volume of liquid = 40 g ÷ 50 cm3 = 0.80 g/cm3.
Points To Remember
- Density of solids changes a lot with a rise in temperature by 20°C to 40°C.
- Density of liquids and gases changes more with the same temperature change because their density decreases and vice versa.
Variation of Density of Liquids and Gases with Temperature
- All matter (solids, liquids, and gases) expands when heated and contracts when cooled, but the change is more in liquids and gases than in solids.
- The change in density for solids is very small with a temperature change of 20°C to 40°C, but for liquids and gases, it is noticeable.
- In liquids and gases, when the temperature rises, their volume increases, but the mass stays the same, so the density decreases.
- For example, if a liquid X has a volume of 50 cm³ and mass of 70 g at 0°C, its density at 0°C = Mass ÷ Volume = 70 g ÷ 50 cm³ = 1.4 g/cm³.
- If the same liquid X at 100°C has a volume of 55 cm³, its density at 100°C = Mass ÷ Volume = 70 g ÷ 55 cm³ = 1.27 g/cm³.
Fun Fact
- The Earth has the highest density among all the planets in our solar system. Its average density is 55100 kg/m³.
The Rate of Change of Motion is Called Speed
- Speed tells us how fast an object moves.
- We calculate speed by dividing the distance covered by the time taken: Speed = Distance ÷ Time.
- If S is the distance covered by the object in time t, then speed v = S ÷ t.
Units of Speed
- In the SI system, the unit of speed is meter per second, written as m/s or ms⁻¹.
Kinds of Speed
(a) Uniform Speed (Howsoever Small the Time Intervals May Be)
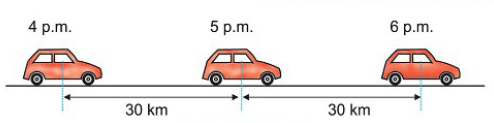
- When an object covers equal distances in equal intervals of time, it is moving with a uniform speed.
- For example, a car covers 30 km every hour from 4 p.m. to 6 p.m., so it is moving with a uniform speed.
- Other examples: An aeroplane flying at 200 km/h or a train running at 90 km/h moves with uniform speed.
(b) Non-uniform Speed or Variable Speed
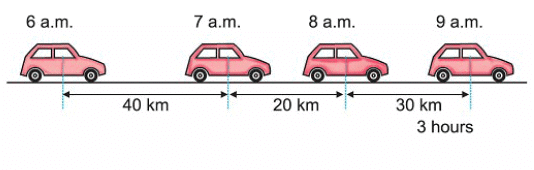
- When an object covers unequal distances in equal intervals of time, it is moving with a non-uniform speed.
- For example, a car covers 40 km from 6 a.m. to 7 a.m., 20 km from 7 a.m. to 8 a.m., and 30 km from 8 a.m. to 9 a.m., so it is moving with a non-uniform speed.
- When an object moves with a non-uniform speed, we calculate its average speed.
- Average speed = Total distance covered ÷ Total time taken to cover the distance.
- In this example, the total distance covered is (40 + 20 + 30) km = 90 km, and the total time taken is 3 hours.
- So, Average speed = 90 km ÷ 3 h = 30 km/h.
Points To Remember
- The unit of area in the Standard International system is square meter (m²).
- The area of a rectangular surface is length × breadth, A = l × b.
- In the Standard International system, volume is measured in cubic meter (m³).
- The smaller unit of volume is cubic centimeter (cm³).
- The smaller unit for measuring volume of liquids is milliliter (ml). One milliliter is equal to one cubic centimeter (symbol 1 cc or 1 cm³).
- Volume of a rectangular slab is the product of its length, breadth, and height, V = l × b × h.
- Volume of liquids is measured by using measuring cylinders, measuring flasks, burettes, pipettes, etc.
- The volume of an irregular solid can be measured with the help of a measuring cylinder by measuring the volume of water displaced by it.
- The mass of a body does not change with the surroundings or position of the body. Mass is found by a physical balance and is never zero for any material body.
- The unit of density in SI system is kg/m³ and in CGS system is g/cm³.
- The density in CGS system = 1000 × Numerical value in SI system.
- The density of liquids and gases changes with change in temperature. With the rise in temperature, the density decreases and vice versa.
- When a body covers equal distances in equal intervals of time (howsoever short the time intervals may be), the body is said to be moving with a uniform speed.
- When a body covers unequal distances in equal intervals of time, the body is said to be moving with a non-uniform speed.
The document Physical Quantities and Measurement Chapter Notes | Physics Class 7 ICSE is a part of the Class 7 Course Physics Class 7 ICSE.
All you need of Class 7 at this link: Class 7
|
7 videos|49 docs|7 tests
|
FAQs on Physical Quantities and Measurement Chapter Notes - Physics Class 7 ICSE
| 1. What is area and how is it measured? |  |
Ans.Area is the amount of space within a shape or a surface. It is measured in square units, such as square meters (m²), square centimeters (cm²), or square kilometers (km²). To find the area of simple shapes, specific formulas are used. For example, the area of a rectangle is calculated by multiplying its length by its width.
| 2. Why is measuring area important in everyday life? |  |
Ans.Measuring area is important for various practical reasons, such as determining the size of land for construction, calculating the amount of paint needed for a wall, or understanding the size of a garden. Accurate area measurements help in planning and resource management in daily activities.
| 3. What are the units of measurement for area? |  |
Ans.The units of measurement for area include square meters (m²), square centimeters (cm²), square feet (ft²), and acres, among others. The choice of unit often depends on the context, such as whether measuring a small room or a large piece of land.
| 4. How do you calculate the area of irregular shapes? |  |
Ans.To calculate the area of irregular shapes, one common method is to divide the shape into regular shapes (like rectangles or triangles), calculate the area of each, and then sum them up. Alternatively, grid paper can be used to estimate the area by counting the number of squares that fit within the shape.
| 5. What is the difference between perimeter and area? |  |
Ans.Perimeter refers to the total distance around the boundary of a shape, while area measures the space contained within that shape. For example, a rectangle may have a large perimeter but a small area if it is very long and narrow. Understanding both concepts is crucial in geometry and real-life applications.
Related Searches
















