Rational Numbers Chapter Notes | Mathematics Class 7 ICSE PDF Download
Introduction
Imagine you're on an adventure, exploring the vast world of numbers! You've already met natural numbers, whole numbers, integers, and fractions, but now it's time to dive deeper into a fascinating group called rational numbers. These numbers are like the superheroes of mathematics, capable of representing everything from the height of a hot air balloon soaring above the clouds to the depth of a whale swimming below the ocean's surface. Rational numbers help us make sense of quantities that aren't just whole or simple fractions, opening up new ways to solve real-world problems. In this chapter, we'll uncover the secrets of rational numbers, learn how to work with them, and see how they fit perfectly on a number line. Get ready to expand your number universe!

Rational Numbers

- Rational numbers are numbers written as a fraction p/q, where p and q are integers and q is not zero.
- The integer p is called the numerator, and q (not zero) is the denominator.
- Every natural number is a rational number because it can be written as n/1 (e.g., 3 = 3/1).
- Not all rational numbers are natural numbers (e.g., 3/5 is not a natural number).
- Every integer is a rational number (e.g., -5 = -5/1), but not all rational numbers are integers (e.g., 3/7).
- Zero is a rational number because it can be written as 0/q (e.g., 0/1, 0/2).
- Every fraction is a rational number since both numerator and denominator are integers, but not all rational numbers are fractions (e.g., 4/-9 has a negative denominator).
- Example: 4/5, -7/9, and 3/4 are rational numbers because they are in the form p/q, where p and q are integers and q ≠ 0.
Positive Rational Numbers
A rational number is positive if both its numerator and denominator are positive or both are negative.
Steps to identify:
- Check the signs of the numerator and denominator.
- If both are positive (e.g., 7/12) or both are negative (e.g., -2/-5), the number is positive.
Negative Rational Numbers
A rational number is negative if its numerator and denominator have opposite signs.
Steps to identify:
- Check the signs of the numerator and denominator.
- If one is positive and the other is negative (e.g., -63/71 or 4/-9), the number is negative.
Absolute Value of a Rational Number
- The absolute value of a rational number is always positive.
- It is calculated by dividing the absolute value of the numerator by the absolute value of the denominator.
- Steps to find absolute value:
- Take the absolute value of the numerator (ignore its sign).
- Take the absolute value of the denominator (ignore its sign).
- Divide the absolute values: |p/q| = |p|/|q|.
- Example: For -3/4, the absolute value is |-3/4| = |-3|/|4| = 3/4.
Equivalent Rational Numbers
- Rational numbers are equivalent if they represent the same value.
- Multiply or divide both numerator and denominator by the same non-zero integer to get equivalent rational numbers.
- Steps to find equivalent rational numbers:
- Choose a non-zero integer n.
- For a rational number p/q, multiply numerator and denominator by n: p × n/q × n.
- Alternatively, divide numerator and denominator by a common factor (if possible): p ÷ n/q ÷ n.
- Example: For 2/3, multiply by 3: 2 × 3/3 × 3 = 6/9. So, 2/3 = 6/9. Similarly, for 14/35, divide by 7: 14 ÷ 7/35 ÷ 7 = 2/5. So, 14/35 = 2/5.
Test of Equality of Two Rational Numbers
Two rational numbers p/q and r/s are equal if p × s = r × q.
Steps to check equality:
- Multiply the numerator of the first number by the denominator of the second: p × s.
- Multiply the numerator of the second number by the denominator of the first: r × q.
- If p × s = r × q, the rational numbers are equal.
Representation of Rational Numbers on a Number Line
Rational numbers can be plotted on a number line similar to integers.
Steps to represent a rational number p/q on a number line:
1. Draw a horizontal line and mark a point as 0 (origin).
2. Mark equal unit lengths to the right (positive) and left (negative) of 0.
3. Divide each unit length into q equal parts (based on the denominator).
4. From 0, move p units to the right (if p is positive) or left (if p is negative) to locate p/q.
- Draw a line and mark 0 as O.

- Mark unit lengths OA (right, +1) and OA' (left, -1).

- Divide OA and OA' into three equal parts.

- Mark the first point to the right of 0 as 1/3 (point P) and the first point to the left as -1/3 (point P').

Standard Form of Rational Numbers
A rational number p/q is in standard form if:
- p and q have no common factors other than 1 (co-prime).
- q is positive.
Steps to convert to standard form:
- Find the greatest common divisor (GCD) of the numerator and denominator.
- Divide both numerator and denominator by their GCD.
- If the denominator is negative, multiply both numerator and denominator by -1 to make the denominator positive.
- GCD of 18 and 24 is 6.
- Divide: 18 ÷ 6 / -24 ÷ 6 = 3 / -4.
- Make denominator positive: 3 × (-1)/-4 × (-1) = -3/4.
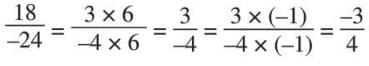
- So, 18 / -24 = -3/4 in standard form.
Comparison of Rational Numbers
Rational numbers can be compared using a number line or by converting them to a common denominator.
Case I: One positive, one negative
- A positive rational number is always greater than a negative rational number.
- Example: 2/3 > -3/2.
Case II: Both positive
- Find the LCM of the denominators.
- Convert both numbers to equivalent fractions with the LCM as the denominator.
- Compare the numerators; the larger numerator indicates the larger number.
Example: Compare 4/5 and 5/7:
- LCM of 5 and 7 is 35.
- Convert: 4/5 = 4 × 7/5 × 7 = 28/35, 5/7 = 5 × 5/7 × 5 = 25/35.
- Compare: 28 > 25, so 4/5 > 5/7.
Case III: Both negative
- Convert each number to have a positive denominator.
- Find the LCM of the denominators.
- Convert to equivalent fractions with the LCM as the denominator.
- Compare the numerators; the larger (less negative) numerator indicates the larger number.
- Convert 1/-3 to -1/3.
- LCM of 12 and 3 is 12.
- Convert: -3/12 = -3/12, -1/3 = -1 × 4/3 × 4 = -4/12.
- Compare: -3 > -4, so -3/12 > -1/3.
Addition of Rational Numbers
Case I: Same denominator
- Ensure both numbers have a positive denominator.
- Add the numerators and keep the denominator the same: p/q + r/q = p + r/q.
Case II: Different denominators
- Ensure both numbers have a positive denominator.
- Find the LCM of the denominators.
- Convert both numbers to equivalent fractions with the LCM as the denominator.
- Add the numerators and keep the common denominator.
- LCM of 19 and 57 is 57.
- Convert: -6/19 = -6 × 3/19 × 3 = -18/57, -2/57 = -2/57.
- Add: -18/57 + -2/57 = -18 + (-2)/57 = -20/57.
Additive Inverse of a Rational Number
The additive inverse of a rational number p/q is -p/q, such that their sum is zero.
Steps to find additive inverse:
- Change the sign of the numerator.
- Keep the denominator the same.
Subtraction of Rational Numbers
Subtracting a rational number means adding its additive inverse. For two rational numbers p/q and r/q.
Case I: Same denominator
- Add the additive inverse: p/q - r/q = p/q + -r/q = p - r/q.
Case II: Different denominators
- Ensure positive denominators.
- Find the LCM of the denominators.
- Convert to equivalent fractions with the LCM as the denominator.
- Subtract by adding the additive inverse of the second number.
- LCM of 12 and 18 is 36.
- Convert: 5/12 = 5 × 3/12 × 3 = 15/36, 13/18 = 13 × 2/18 × 2 = 26/36.
- Subtract: 15/36 - 26/36 = 15/36 + -26/36 = 15 - 26/36 = -11/36.
Multiplication of Rational Numbers
Multiply rational numbers by multiplying numerators and denominators separately: p/q × r/s = p × r/q × s.
Points to remember:
- To multiply a rational number by an integer, treat the integer as a fraction: p/q × r = p × r/q.
- Multiplication is commutative: p/q × r/s = r/s × p/q.
- Multiplying by 0 gives 0: p/q × 0 = 0.
Steps to multiply:
- Multiply the numerators to get the new numerator.
- Multiply the denominators to get the new denominator.
- Simplify the result if possible.
- Multiply numerators: 9 × (-7) = -63.
- Multiply denominators: 4 × 5 = 20.
- Result: -63/20.
Reciprocal of a Rational Number
- The reciprocal of a non-zero rational number p/q is q/p, where p ≠ 0 and q ≠ 0.
- It is also called the multiplicative inverse because their product is 1.
Steps to find reciprocal:
- Swap the numerator and denominator.
- Ensure the result is in standard form if needed.
Division of Rational Numbers
To divide a rational number by a non-zero rational number, multiply the first number by the reciprocal of the second.
Steps to divide p/q ÷ r/s:
- Find the reciprocal of the second number: r/s becomes s/r.
- Multiply: p/q × s/r = p × s/q × r.
- Simplify the result if possible.
- Reciprocal of -2/5 is 5/-2.
- Multiply: 3/-4 × 5/-2 = 3 × 5/-4 × -2 = 15/8.
Decimal Representation of Rational Numbers
Rational numbers can be converted into decimals using long division.
Types of decimals:
Terminating decimals: Have a finite number of digits after the decimal point.
Non-terminating decimals:
- Recurring (repeating): Digits repeat in a pattern endlessly.
- Non-recurring: Digits continue infinitely without repeating; these represent irrational numbers.
- A rational number gives a terminating decimal if the prime factors of its denominator (in simplest form) are only 2 or 5.
- All rational numbers are either terminating or non-terminating recurring decimals.
- Irrational numbers are non-terminating and non-recurring decimals.
Steps to convert a rational number to a decimal:
- Divide the numerator by the denominator using long division.
- Observe if the decimal terminates (stops) or repeats a pattern.
- If it repeats, write it with a bar over the repeating digits (e.g., 0.18).
- Divide 2 by 11: 2 ÷ 11 = 0.181818….
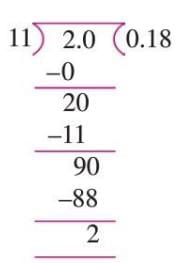
- The remainder 2 repeats, so the digits 18 repeat.
- Write as
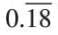 , meaning 18 repeats forever.
, meaning 18 repeats forever.
|
47 videos|118 docs|23 tests
|
FAQs on Rational Numbers Chapter Notes - Mathematics Class 7 ICSE
| 1. What are rational numbers and how are they different from integers? |  |
| 2. How do you determine the absolute value of a rational number? |  |
| 3. What are equivalent rational numbers and how can they be found? |  |
| 4. How can you test the equality of two rational numbers? |  |
| 5. How are rational numbers represented on a number line? |  |





















