Triangles Chapter Notes | Mathematics Class 7 ICSE PDF Download
| Table of contents |

|
| Introduction |

|
| Triangle |

|
| Classification of Triangles |

|
| Properties of Triangles |

|
| Altitude and Median of a Triangle |

|
| Pythagoras Property (or Pythagoras Theorem) |

|
Introduction
Triangles are fascinating shapes that form the backbone of many structures and systems around us. From the sturdy frame of a bicycle to the precise calculations of GPS navigation, triangles are everywhere, offering strength and stability. Their unique properties make them a favorite among architects and engineers. In this chapter, we dive into the world of triangles, exploring their types, properties, and the famous Pythagoras theorem that unlocks the secrets of right-angled triangles. Get ready to uncover the magic of these three-sided wonders and see how they shape the world!
Triangle
- A triangle is a shape with three straight sides that enclose a region, called the triangular region.
- It is represented as △ABC, where A, B, and C are its vertices.
Sides
- The three line segments that make up a triangle are its sides.
- In △ABC, the sides are AB, BC, and CA.
Vertices
- Vertices are the points where two sides of a triangle meet.
- In △ABC, the vertices are A, B, and C.
- Each vertex is opposite to one side: A is opposite BC, B is opposite CA, and C is opposite AB.
Example: In △ABC, vertex A is opposite side BC, vertex B is opposite side CA, and vertex C is opposite side AB.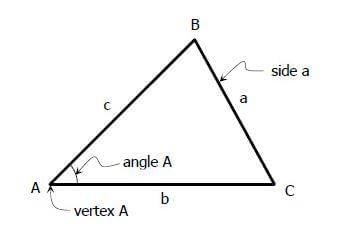 Triangle Structure
Triangle Structure
Angles
- Angles are formed where two sides of a triangle meet, called interior angles.
- In △ABC, the interior angles are ∠ABC (at B), ∠BCA (at C), and ∠CAB (at A).
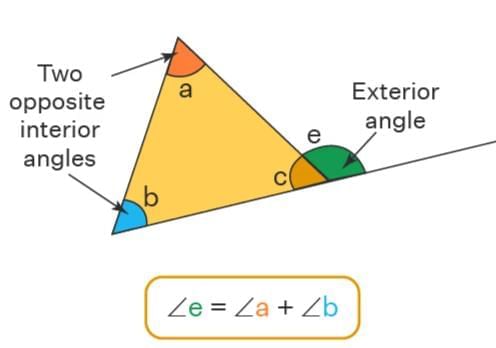
- An exterior angle is formed when a side is extended outside the triangle.
- Each vertex has two equal exterior angles due to vertically opposite angles.
Example: In △ABC, if side AB is extended to D, ∠ABD is an exterior angle at B. If CB is extended to E, ∠CBE is another exterior angle, and ∠ABD = ∠CBE as they are vertically opposite.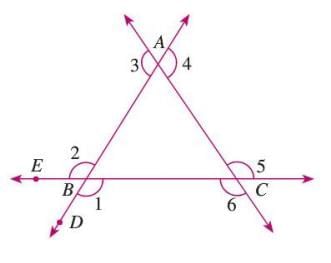
Relation between an exterior angle and its interior opposite angles
An exterior angle of a triangle equals the sum of its two interior opposite angles.
Stepwise Explanation:
- Extend a side of the triangle to form an exterior angle.
- Identify the two interior angles opposite to this exterior angle.
- Use the property that the exterior angle equals the sum of these two interior angles.
- Verify using the fact that the exterior angle and its adjacent interior angle form a linear pair (180°).
Example: In △ABC, side CB is extended to D, forming exterior angle ∠ABD. The interior opposite angles are ∠BCA and ∠CAB. Thus, ∠ABD = ∠BCA + ∠CAB.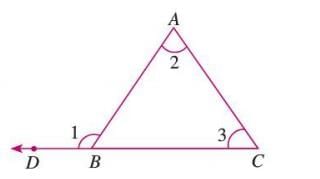
Classification of Triangles
Triangles are classified based on the lengths of their sides or the sizes of their angles.
On the basis of sides
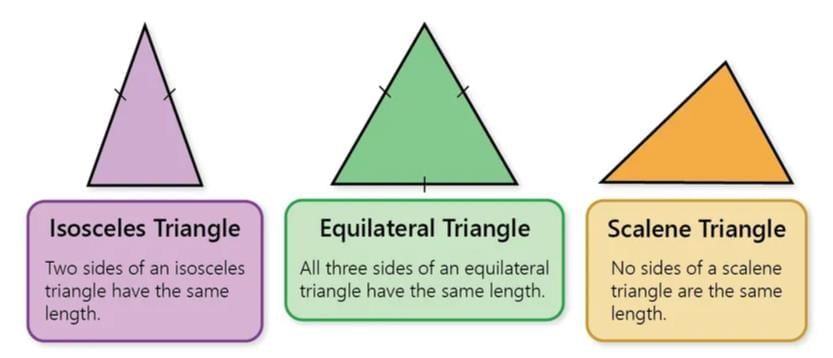
- Isosceles triangle: A triangle with two equal sides. The third side is the base, and angles opposite the equal sides are base angles. The angle opposite the base is the vertical angle.
- Scalene triangle: A triangle with all sides of different lengths.
- Equilateral triangle: A triangle with all three sides equal.
On the basis of angles
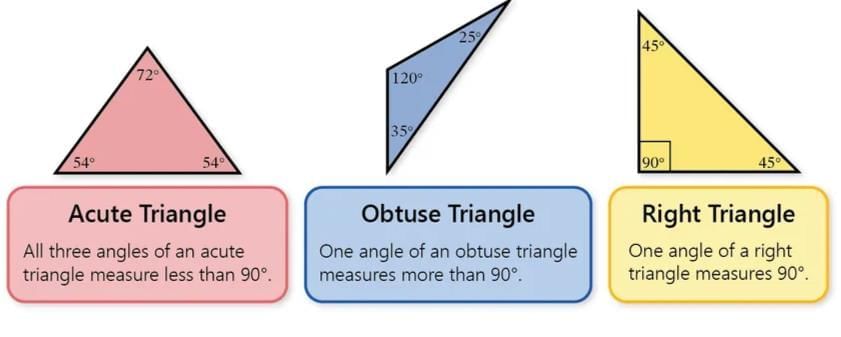
- Acute-angled triangle: A triangle with all angles less than 90°.
- Obtuse-angled triangle: A triangle with one angle greater than 90°.
- Right-angled triangle: A triangle with one angle equal to 90°. The side opposite the right angle is the hypotenuse.
- An isosceles right-angled triangle has two equal sides, but the hypotenuse is always longer.
Properties of Triangles
Property 1: The sum of the three angles in a triangle is always 180°.
Example: In △ABC, draw line PQ parallel to BC through A. Since PQ || RS (extended BC), ∠ABC = ∠PAB and ∠ACB = ∠QAC (alternate angles). Thus, ∠PAB + ∠BAC + ∠QAC = 180°, proving ∠ABC + ∠BAC + ∠ACB = 180°.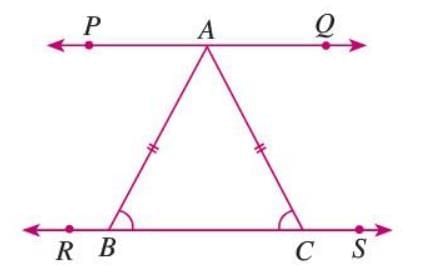
Property 2: If two sides of a triangle are equal, the angles opposite them are equal, and vice versa.
Example: In isosceles △ABC with AB = AC, ∠ABC = ∠ACB. In an isosceles right-angled triangle with ∠C = 90° and AC = BC, ∠BAC = ∠CBA = 45°.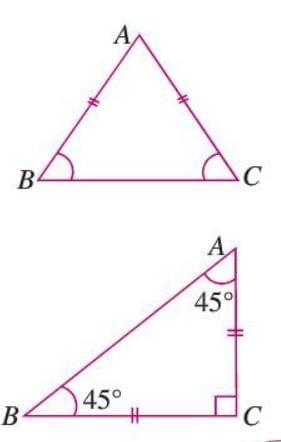
Property 3: The sum of any two sides of a triangle is always greater than the third side.
Example: In △PQR, verify that PQ + QR > PR, PQ + PR > QR, and QR + PR > PQ.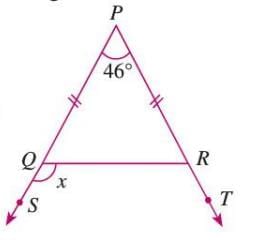
Additional Points:
- In an isosceles triangle, equal sides have equal opposite angles.
- In an equilateral triangle, all sides are equal, and all angles are 60°.
- In a scalene triangle, all sides and angles are unequal.
- If all angles are equal, the triangle is equilateral.
Altitude and Median of a Triangle
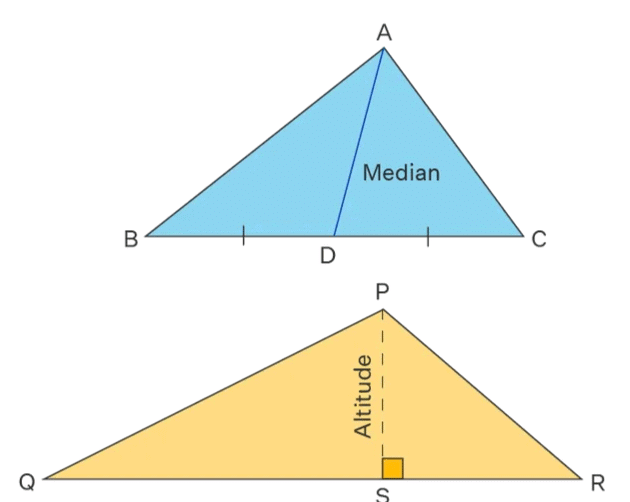
- Altitude: A perpendicular line from a vertex to the opposite side (or its extension).
- A triangle has three altitudes, and they meet at a point called the orthocentre.
- Median: A line from a vertex to the midpoint of the opposite side.
- A triangle has three medians, and they meet at a point called the centroid.
- The orthocentre may be inside or outside the triangle, but the centroid is always inside.
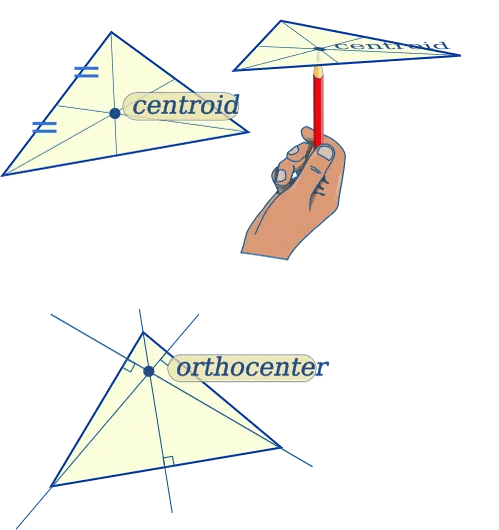
Stepwise Explanation:
- For altitude, draw a perpendicular from a vertex to the opposite side.
- Identify the orthocentre as the point where all three altitudes meet.
- For median, find the midpoint of the opposite side and draw a line from the vertex to it.
- Identify the centroid as the point where all three medians meet.
Pythagoras Property (or Pythagoras Theorem)
- In a right-angled triangle, the square of the hypotenuse equals the sum of the squares of the other two sides (legs).
- The hypotenuse is the side opposite the right angle, and the legs are the sides containing the right angle.
Stepwise Explanation:
- Identify the right angle and the hypotenuse.
- Label the legs as the other two sides.
- Apply the formula: (Hypotenuse)2 = (Leg1)2 + (Leg2)2.
Verification of Pythagoras Property
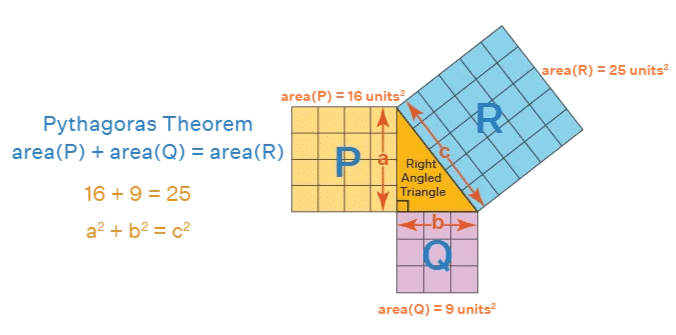
The Pythagoras property can be verified using graph paper by comparing areas of squares on the sides.
Stepwise Explanation:
- Draw a right-angled triangle on graph paper.
- Construct squares on the hypotenuse and the two legs.
- Count the unit squares in each square.
- Check that the number of unit squares on the hypotenuse equals the sum of unit squares on the legs.
Converse of Pythagoras Property
If the square of one side equals the sum of the squares of the other two sides, the triangle is right-angled, with the right angle opposite the longest side.
Example: For sides 1.5 cm, 2 cm, and 2.5 cm, check: 1.52 + 22 = 2.25 + 4 = 6.25 = 2.52. Thus, it’s a right-angled triangle with the right angle opposite the 2.5 cm side.
Pythagorean Triplet

A set of three numbers where the square of the largest equals the sum of the squares of the other two is a Pythagorean triplet.
Stepwise Explanation:
- Identify three numbers representing the sides of a triangle.
- Check if the square of the largest number equals the sum of the squares of the other two.
- If true, the numbers form a Pythagorean triplet.
Example: The numbers (3, 4, 5) form a Pythagorean triplet because 52 = 25 and 32 + 42 = 9 + 16 = 25.
|
47 videos|144 docs|23 tests
|
FAQs on Triangles Chapter Notes - Mathematics Class 7 ICSE
| 1. What are the different classifications of triangles based on their sides? |  |
| 2. How can the properties of triangles be useful in real-life situations? |  |
| 3. What is the difference between the altitude and median of a triangle? |  |
| 4. Can you explain the Pythagorean Theorem and its application in triangles? |  |
| 5. How can one find the area of a triangle using its base and height? |  |















