Compound Interest (Using Formula) Chapter Notes | Mathematics Class 9 ICSE PDF Download
Introduction
Imagine you have some money saved up, and instead of keeping it under your mattress, you decide to invest it in a bank that promises to grow your money over time. This growth doesn't just add a fixed amount each year but builds on itself, like a snowball rolling down a hill, getting bigger and bigger. This is the magic of compound interest! In this chapter, we'll explore how to calculate compound interest using simple formulas, making it easier to find out how much your money can grow over time or solve related problems. Whether it's figuring out the future value of an investment or determining how long it takes for money to double, these notes will guide you through the concepts step-by-step, making them clear and exciting to learn!

- Compound interest is the interest calculated on the initial principal and the accumulated interest from previous periods.
- It differs from simple interest, where interest is calculated only on the initial amount.
- The principal grows each period as interest is added, making future interest calculations larger.
- Calculating compound interest manually for many periods can be time-consuming.
- Formulas simplify the process, allowing quick and accurate calculations for amount and interest.
Using Formula
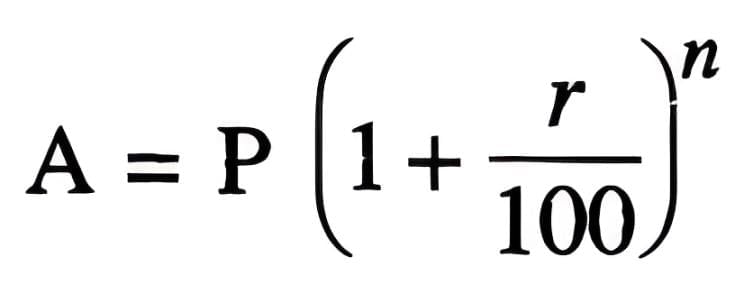
- Formulas make calculating compound interest faster and easier, especially for multiple periods.
- The main formula is used when interest is compounded annually.
Steps to use the formula:
- Identify the principal (P), rate of interest (r), and time period (n).
- Apply the formula to find the amount (A).
- Subtract the principal from the amount to find the compound interest (C.I.).
- Given: P = ₹7,500, n = 2 years, r = 6%.
- Formula: A = P(1 + r/100)n.
- Substitute: A = ₹7,500 × (1 + 6/100)2 = ₹7,500 × (106/100)2.
- Calculate: A = ₹7,500 × (1.06)2 = ₹7,500 × 1.1236 = ₹8,427.
- Compound Interest = A - P = ₹8,427 - ₹7,500 = ₹927.
When the Rates for Successive Years are Different
- If interest rates change each year, the formula adjusts to multiply factors for each year's rate.
- Formula:
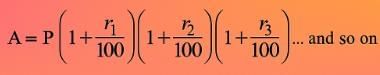
- where r1, r2, r3 are rates for successive years.
Steps:
- Identify the principal and the rates for each year.
- Multiply the principal by each year's factor (1 + r/100).
- Calculate the final amount and subtract the principal for compound interest.
- Given: P = ₹12,000, r1 = 8%, r2 = 10%, r3 = 15%.
- Formula: A = P(1 + r1/100)(1 + r2/100)(1 + r3/100).
- Substitute: A = ₹12,000 × (1 + 8/100)(1 + 10/100)(1 + 15/100).
- Calculate: A = ₹12,000 × (108/100) × (110/100) × (115/100) = ₹12,000 × 1.08 × 1.1 × 1.15 = ₹16,394.40.
- Compound Interest = ₹16,394.40 - ₹12,000 = ₹4,394.40.
Inverse Problems
- Inverse problems involve finding the principal, rate, or time given the amount or interest.
- Use the compound interest formula and rearrange it to solve for the unknown variable.
To Find the Principal
Use the formula A = P(1 + r/100)n and solve for P.
Steps:
- Rearrange: P = A / (1 + r/100)n.
- Substitute known values of A, r, and n.
- Simplify to find P.
- Given: A = ₹3,630, r = 10%, n = 2 years.
- Formula: P = A / (1 + r/100)n.
- Substitute: P = ₹3,630 / (1 + 10/100)2 = ₹3,630 / (11/10)2.
- Calculate: P = ₹3,630 × (10/11) × (10/11) = ₹3,630 × 100/121 = ₹3,000.
To Find the Rate Percent
Use A = P(1 + r/100)n and solve for r.
Steps:
- Rearrange: (1 + r/100)n = A/P.
- Take the n-th root: 1 + r/100 = (A/P)1/n.
- Solve for r: r = [(A/P)1/n - 1] × 100.
- Given: P = ₹2,000, A = ₹2,315.25, n = 3 years.
- Formula: A = P(1 + r/100)n.
- Rearrange: (1 + r/100)3 = 2,315.25 / 2,000 = 1.157625.
- Take cube root: 1 + r/100 = (1.157625)1/3 = 21/20.
- Solve: r/100 = 21/20 - 1 = 1/20, so r = 5%.
To Find the Number of Years (i.e., Time)
Use A = P(1 + r/100)n and solve for n.
Steps:
- Rearrange: (A/P) = (1 + r/100)n.
- Compare powers to find n, often by trial or simplification.
- Given: P = ₹2,000, A = ₹2,662, r = 10%.
- Formula: A = P(1 + r/100)n.
- Rearrange: 2,662/2,000 = (1 + 10/100)n = (11/10)n.
- Simplify: 1.331 = (11/10)n.
- Since (11/10)3 = 1.331, n = 3 years.
When the Interest is Compounded Half-Yearly (Two Times in a Year)
- When interest is compounded half-yearly, the rate is halved, and the number of periods is doubled.
- Formula: A = P(1 + r/(2 × 100))n × 2.
Steps:
- Divide the annual rate by 2.
- Multiply the number of years by 2 for the number of periods.
- Calculate the amount and subtract principal for compound interest.
- Given: P = ₹4,000, r = 10%, n = 1.5 years.
- Formula: A = P(1 + r/(2 × 100))n × 2.
- Substitute: A = ₹4,000 × (1 + 10/(2 × 100))1.5 × 2 = ₹4,000 × (1 + 0.05)3.
- Calculate: A = ₹4,000 × (1.05)3 = ₹4,630.50.
- Compound Interest = ₹4,630.50 - ₹4,000 = ₹630.50.
When the Time is Not an Exact Number of Years and the Interest is Compounded Yearly
- For non-integer years (e.g., 2.5 years), calculate for whole years, then treat the remaining fraction as a half-year period.
- Formula for 2.5 years: A = P(1 + r/100)2(1 + r/(2 × 100))1.
Steps:
- Calculate amount for whole years using A = P(1 + r/100)n.
- Use the result as principal for the remaining half-year with half-yearly formula.
- Combine to find the total amount.
- Given: P = ₹10,000, r = 10%, n = 2.5 years.
- Step 1: For 2 years, A = ₹10,000 × (1 + 10/100)2 = ₹10,000 × (1.1)2 = ₹12,100.
- Step 2: For remaining 0.5 years, use P = ₹12,100, A = ₹12,100 × (1 + 10/(2 × 100))1 = ₹12,100 × 1.05 = ₹12,705.
- Total Amount = ₹12,705.
Other Applications of the Formula
- The compound interest formula can be applied to growth and depreciation scenarios.
- It is used for problems involving population growth, industrial growth, or asset depreciation.
Growth
The formula A = P(1 + r/100)n is used for growth in industries, population, or inflation.
Steps:
- Identify initial value (P), growth rate (r), and time (n).
- Apply the formula to find the final value (A).
- Given: P = 1,600, r = 20%, n = 2 years.
- Formula: A = P(1 + r/100)n.
- Substitute: A = 1,600 × (1 + 20/100)2 = 1,600 × (1.2)2.
- Calculate: A = 1,600 × 1.44 = 2,304 industries.
Depreciation
- Depreciation reduces an asset's value annually at a fixed rate.
- Formula: Value after n years = P(1 - r/100)n.
Steps:
- Identify initial value (P), depreciation rate (r), and time (n).
- Apply the formula to find the final value.
- Given: Initial value = ₹2,50,000, final value = ₹1,28,000, r = 20%.
- Formula: A = P(1 - r/100)n.
- Substitute: 1,28,000 = 2,50,000 × (1 - 20/100)n = 2,50,000 × (0.8)n.
- Simplify: (0.8)n = 1,28,000 / 2,50,000 = 0.512.
- Since (0.8)3 = 0.512, n = 3 years.
Population Problems
Use A = P(1 + r/100)n for population growth, where P is the initial population.
Steps:
- Identify initial population (P), growth rate (r), and time (n).
- Calculate future or past population using the formula.
- Given: P = 2,16,000, r = 20%, n = 2 years.
- Formula: A = P(1 + r/100)n.
- Substitute: A = 2,16,000 × (1 + 20/100)2 = 2,16,000 × (1.2)2.
- Calculate: A = 2,16,000 × 1.44 = 3,11,040.
|
28 videos|171 docs|28 tests
|
FAQs on Compound Interest (Using Formula) Chapter Notes - Mathematics Class 9 ICSE
| 1. What is the formula for calculating compound interest? |  |
| 2. How do I calculate compound interest when it is compounded half-yearly? |  |
| 3. What should I do if the time period for investment is not a whole number of years and interest is compounded yearly? |  |
| 4. Can you explain what inverse problems are in the context of compound interest? |  |
| 5. What are some other applications of the compound interest formula beyond finance? |  |
















