Indices (Exponents) Chapter Notes | Mathematics Class 9 ICSE PDF Download
| Table of contents |

|
| Introduction |

|
| Laws of Indices |

|
| Handling Positive, Fractional, Negative, and Zero Indices |

|
| Simplification of Expressions |

|
| Using Laws of Exponents |

|
| Rule table |

|
Introduction
Imagine a world where numbers can grow or shrink with a single, powerful twist! That's the magic of indices, or exponents, in mathematics. This chapter takes you on an exciting journey through the concept of exponents, where you'll learn how to simplify complex calculations, handle positive, negative, and even fractional powers, and apply these rules to solve intriguing problems. Whether it's multiplying numbers raised to powers or simplifying tricky expressions, indices make math both fun and efficient. Get ready to unlock the secrets of exponents and see numbers in a whole new way!

- Indices, also called exponents, represent repeated multiplication of a number by itself.
- A term like a × a × a ... (m times) is written as am, where 'a' is the base and 'm' is the exponent or index.
- The expression am is read as "a raised to the power m" or "a to the power m."
- The base is the number being multiplied, and the exponent tells how many times it is multiplied by itself.
Laws of Indices
- Indices follow specific rules to simplify expressions involving powers.
- These laws help in performing operations like multiplication, division, and raising powers to another power.
First Law (Product Law)
- When multiplying two powers with the same base, add the exponents: am × an = am+n.
- Example: a7 × a4 = a7+4 = a11.
Second Law (Quotient Law)
- When dividing two powers with the same base, subtract the exponents: am ÷ an = am-n.
- Example: a7 ÷ a4 = a7-4 = a3.
Third Law (Power Law)
- When a power is raised to another power, multiply the exponents: (am)n = am×n.
- Example: (a3)4 = a3×4 = a12.
Handling Positive, Fractional, Negative, and Zero Indices
Exponents can be positive, negative, fractional, or zero, each with specific rules for simplification.
1. Power of a Product and Quotient
- For a product raised to a power: (a × b)m = am × bm.
- For a quotient raised to a power: (a ÷ b)m = am ÷ bm.
- Example: (2 × 3)5 = 25 × 35.
2. Fractional Indices
- A fractional exponent represents a root: a1/n = n√a (nth root of a), where a ≠ 0.
- For example, a1/2 is the square root, a1/3 is the cube root, and so on.
- Example: √a = a1/2, so √2 = 21/2.
3. General Fractional Indices
- An exponent like am/n means the nth root of a raised to the power m: am/n = n√(am).
- Conversely, n√(am) = am/n.
- Example: a4/5 = 5√(a4).
4. Negative Indices
- A negative exponent represents the reciprocal: a-n = 1 ÷ an and an = 1 ÷ a-n, where a ≠ 0.
- Example: a-3 = 1 ÷ a3.
5. Zero Index
- Any non-zero number raised to the power zero equals 1: a0 = 1, where a ≠ 0.
- Example: 50 = 1.
6. Negative Base with Even and Odd Exponents
- If the base is negative and the exponent is even, the result is positive: (-a)m = am.
- If the base is negative and the exponent is odd, the result is negative: (-a)m = -am.
- Example: (-2)4 = 24, but (-2)5 = -25.
Simplification of Expressions
- Using the laws of indices, complex expressions can be simplified step-by-step.
- Break down the expression, apply the appropriate laws, and combine terms.
- Step 1: Write 27 as 33, so (27)-1/3 = (33)-1/3.
- Step 2: Apply the power law: (33)-1/3 = 33×(-1/3) = 3-1.
- Step 3: Convert negative exponent: 3-1 = 1 ÷ 3 = 1/3.
- Answer: 1/3.
Using Laws of Exponents
- Exponents are used to solve equations and prove relationships by applying the laws of indices.
- Equations with exponents can be solved by equating bases or exponents, or by substituting variables.
- Proofs involve manipulating expressions to show equality using index laws.
- Step 1: Express 9 and 27 as powers of 3: 9 = 32, 27 = 33.
- Step 2: Rewrite the equation: 32 × 3x = (33)2x-5.
- Step 3: Simplify: 32+x = 33(2x-5) = 36x-15.
- Step 4: Equate exponents (since bases are same): 2 + x = 6x - 15.
- Step 5: Solve: x + 2 = 6x - 15 → 17 = 5x → x = 17/5 = 3 2/5.
- Answer: x = 3 2/5.
Rule table
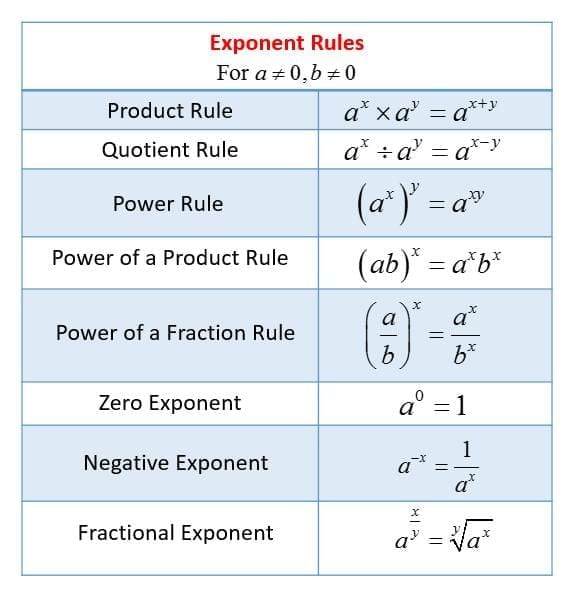
|
64 videos|136 docs|28 tests
|
FAQs on Indices (Exponents) Chapter Notes - Mathematics Class 9 ICSE
| 1. What are the basic laws of indices that I should know for Class 9? |  |
| 2. How do I handle fractional indices in mathematical expressions? |  |
| 3. What is the significance of zero indices in exponential expressions? |  |
| 4. Can you explain how to simplify expressions involving negative indices? |  |
| 5. How can I use the laws of exponents to solve complex expressions? |  |















