Logarithms Chapter Notes | Mathematics Class 9 ICSE PDF Download
Introduction
Imagine a world where complex calculations become as simple as adding or subtracting numbers! That's the magic of logarithms, a powerful mathematical tool that transforms multiplication into addition, division into subtraction, and powers into simpler forms. In this chapter, we'll dive into the fascinating world of logarithms, exploring how they help us express relationships between numbers in a new way, making calculations easier and more intuitive. Whether you're solving exponential equations or simplifying large numbers, logarithms are like a shortcut that unlocks the secrets of numbers. Let's embark on this journey to understand logarithms step by step!
Logarithms
- Logarithms simplify complex calculations involving exponents.
- They express the relationship between a base, an exponent, and a result in a different form.
- If ab = c, then logac = b, where a ≠ 1.
- This is read as "logarithm of c to the base a is b."
- The exponential form (ab = c) and logarithmic form (logac = b) are interchangeable.
Explanation:
- Here, 3 is the base, 4 is the exponent, and 81 is the result.
- In logarithmic form, log381 = 4 means the exponent 4 is needed to raise 3 to get 81.
Interchanging (Logarithmic form vis-à-vis exponential form)
- Exponential form is ab = c, where a is the base, b is the exponent, and c is the result.
- Logarithmic form is logac = b, showing the same relationship differently.
- Logarithm of 1 to any base is always 0 (since a0 = 1).
- Logarithm of a number to its own base is always 1 (since a1 = a).
Explanation:
- Exponential form: 2-3 = 1/23 = 1/8 = 0.125.
- Logarithmic form: log20.125 = -3 means raising 2 to the power -3 gives 0.125.
Laws of Logarithm with Use
Logarithm laws help simplify expressions involving products, quotients, and powers.
First Law (Product Law)
- The logarithm of a product is the sum of the logarithms of its factors with the same base.
- Formula: loga(m × n) = logam + logan.
- This applies to multiple factors: loga(m × n × p) = logam + logan + logap.
- Note: loga(m + n) ≠ logam + logan.
Explanation:
- If m = 2 and n = 3, then loga(2 × 3) = loga6.
- By the product law, loga6 = loga2 + loga3.
Second Law (Quotient Law)
- The logarithm of a fraction is the logarithm of the numerator minus the logarithm of the denominator, both with the same base.
- Formula: loga(m/n) = logam - logan.
- Note: logam / logan ≠ logam - logan, and loga(m - n) ≠ logam - logan.
Explanation:
- If m = 10 and n = 2, then loga(10/2) = loga5.
- By the quotient law, loga5 = loga10 - loga2.
Third Law (Power Law)
- The logarithm of a number raised to a power is the power times the logarithm of the number with the same base.
- Formula: loga(mn) = n logam.
- Corollary: For roots, loga(m1/n) = (1/n) logam.
Explanation:
- If m = 2 and n = 3, then loga(23) = loga8.
- By the power law, loga8 = 3 loga2.
Additional Notes
- Logarithms to base 10 are called common logarithms.
- If no base is specified, the base is assumed to be 10 (e.g., log 8 = log108).
- log101 = 0, log1010 = 1, log10100 = 2, log101000 = 3, etc.
Explanation:
- Since 100 = 102, log10100 = log10(102).
- By the power law, log10(102) = 2 log1010 = 2 × 1 = 2.
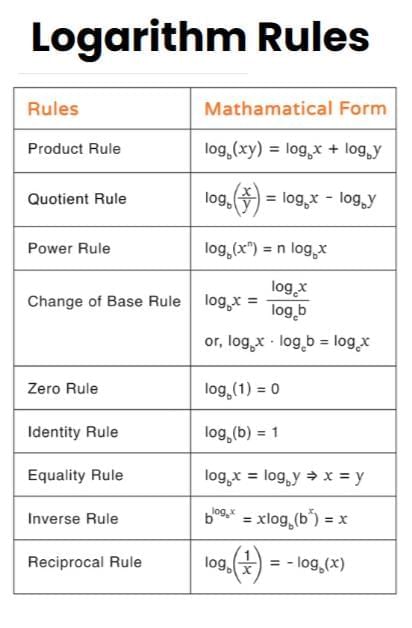
Expansion of Expressions with the Help of Laws of Logarithms
- Logarithm laws are used to expand or combine logarithmic expressions.
- Product law breaks products into sums, quotient law handles fractions, and power law handles exponents.
- Conversely, logarithmic sums or differences can be combined into a single logarithm.
Explanation:
- Write log y = log((a4 × b2) / c3).
- Apply quotient law: log((a4 × b2) / c3) = log(a4 × b2) - log c3.
- Apply product law: log(a4 × b2) = log a4 + log b2.
- Apply power law: log a4 = 4 log a, log b2 = 2 log b, log c3 = 3 log c.
- Combine: log y = 4 log a + 2 log b - 3 log c.
More About Logarithms
Logarithms have additional properties that relate bases and arguments.
Property 1: Reciprocal Relationship
- If logba = x, then logab = 1/x.
- This shows that the logarithm of a to base b is the reciprocal of the logarithm of b to base a.
Explanation:
- Since 23 = 8, log28 = 3.
- Since 81/3 = 2, log82 = 1/3.
- Thus, log28 = 1 / log82.
Property 2: Product of Reciprocal Logarithms
- logba × logab = 1.
- This follows from the reciprocal relationship.
Explanation:
- Since logba = 1 / logab, we have log53 = 1 / log35.
- Thus, log53 × log35 = (1 / log35) × log35 = 1.
Property 3: Logarithm of a Base to Itself
- logaa = 1, so loga(ax) = x.
- This is because raising a base to a power x gives ax, and the logarithm reverses this.
Explanation:
- Since 25 = 32, log232 = log2(25).
- By the power law, log2(25) = 5 log22 = 5 × 1 = 5.
Property 4: Change of Base
- logba = (logxa) / (logxb), where x is any positive number.
- This allows logarithms with different bases to be expressed in terms of a common base.
Explanation:
- log101000 = log10(103) = 3.
- log10100 = log10(102) = 2.
- By change of base, log1001000 = 3/2.
|
28 videos|171 docs|28 tests
|
FAQs on Logarithms Chapter Notes - Mathematics Class 9 ICSE
| 1. What is the difference between logarithmic form and exponential form? |  |
| 2. What are the main laws of logarithms? |  |
| 3. How can we expand expressions using the laws of logarithm? |  |
| 4. Why are logarithms important in mathematics and science? |  |
| 5. Can you give an example of using logarithms in solving equations? |  |
















