Triangles Chapter Notes | Mathematics Class 9 ICSE PDF Download
| Table of contents |

|
| Introduction |

|
| Relation Between Sides And Angles Of Triangles |

|
| Some Important Terms |

|
| Congruent Triangles |

|
| Conditions for Congruency of Triangles |

|
Introduction
Triangles are fascinating shapes that form the foundation of geometry, and understanding their properties opens up a world of mathematical wonders! In this chapter, we dive into the concept of congruency in triangles, exploring how two triangles can be identical in shape and size. We'll learn about the relationships between sides and angles, special lines like medians and altitudes, and the conditions that make triangles congruent. By the end, you'll see how these ideas help us prove fascinating geometric relationships with clarity and precision!

- A triangle is a shape formed by three straight lines, creating three sides and three vertices.
- Example: In triangle ABC, the vertices are A, B, and C, and the sides are AB, BC, and CA.
Relation Between Sides And Angles Of Triangles
Rule 1: Different Side Lengths, Different Angles
- If all sides of a triangle are of different lengths, the angles opposite these sides are also different.
- The larger the side, the larger the angle opposite to it.
Stepwise Explanation:
- Compare the lengths of the sides of a triangle.
- Identify the angles opposite each side.
- Note that the largest side faces the largest angle, the second largest side faces the second largest angle, and so on.
Example: In triangle ABC, if AC > BC > AB, then the angle opposite AC (angle B) is greater than the angle opposite BC (angle A), which is greater than the angle opposite AB (angle C). So, angle B > angle A > angle C.
Rule 2: Different Angles, Different Side Lengths
- If all angles of a triangle are different, the sides opposite these angles are also different.
- The larger the angle, the longer the side opposite to it.
Stepwise Explanation:
- Compare the measures of the angles in a triangle.
- Identify the sides opposite each angle.
- The largest angle is opposite the longest side, the second largest angle is opposite the second longest side, and so on.
Example: In triangle ABC, if angle C > angle A > angle B, then the side opposite angle C (AB) is longer than the side opposite angle A (BC), which is longer than the side opposite angle B (AC). So, AB > BC > AC.
Rule 3: Equal Sides, Equal Angles
- If two sides of a triangle are equal, the angles opposite these sides are also equal.
- Conversely, if two angles are equal, the sides opposite them are equal.
Stepwise Explanation:
- Check if any two sides of a triangle are equal in length.
- If they are, the angles opposite those sides are equal.
- Alternatively, check if any two angles are equal.
- If they are, the sides opposite those angles are equal.
Formulas:
- If AB = AC, then angle B = angle C.
- If angle B = angle C, then AB = AC.
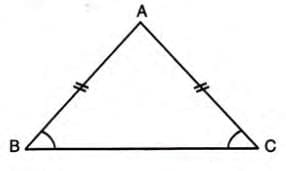
Example: In triangle ABC, if AB = AC, then angle B = angle C. Conversely, if angle B = angle C, then AB = AC.
Rule 4: All Sides Equal, All Angles Equal
- If all sides of a triangle are equal, all angles are equal (equilateral triangle).
- Conversely, if all angles are equal, all sides are equal.
Stepwise Explanation:
- Verify if all three sides of a triangle are equal.
- If yes, all three angles are equal (each 60° in an equilateral triangle).
- Alternatively, verify if all three angles are equal.
- If yes, all three sides are equal.
Formulas:
- If AB = BC = AC, then angle A = angle B = angle C.
- If angle A = angle B = angle C, then AB = BC = AC.
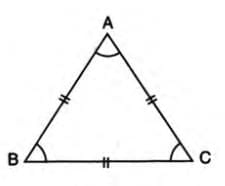
Example: In triangle ABC, if AB = BC = AC, then angle A = angle B = angle C. Conversely, if angle A = angle B = angle C, then AB = BC = AC.
Some Important Terms
Median
A median is a line from a vertex to the midpoint of the opposite side.
Stepwise Explanation:
- Identify a side of the triangle.
- Find the midpoint of that side.
- Draw a line from the opposite vertex to this midpoint.
- This line is the median for that side.
Example:
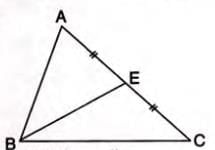
Properties of Medians
- A triangle has three medians, one for each side.
- All three medians intersect at a single point called the centroid.
- The centroid divides each median in the ratio 2:1 (longer segment towards the vertex).
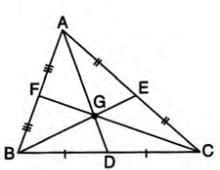
Stepwise Explanation:
- Draw all three medians of a triangle.
- Locate their intersection point, which is the centroid.
- Measure the segments of each median from the vertex to the centroid and from the centroid to the midpoint.
- The ratio of these segments is 2:1.
Formula:
- For median AD, AG:GD = 2:1, where G is the centroid.
- Similarly, BG:GE = 2:1 and CG:GF = 2:1.
Altitude
An altitude is a perpendicular line from a vertex to the line containing the opposite side.
Stepwise Explanation:
- Choose a vertex of the triangle.
- Draw a perpendicular line from this vertex to the opposite side (or its extension).
- This line is the altitude for that side.
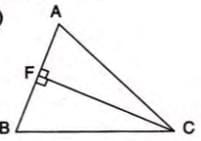
Example: In triangle ABC, CF is the altitude from vertex C to side AB, where CF is perpendicular to AB.
Congruent Triangles
Two triangles are congruent if they have the same shape and size, meaning all corresponding angles and sides are equal.
Stepwise Explanation:
- Check if all angles of one triangle equal the corresponding angles of another.
- Check if all sides of one triangle equal the corresponding sides of the other.
- If both conditions are met, the triangles are congruent and can be superimposed perfectly.
Key Points:
- Congruent triangles coincide exactly when placed over each other.
- Corresponding sides are opposite equal angles, and corresponding angles are opposite equal sides.
- Corresponding Parts of Congruent Triangles are Congruent (C.P.C.T.C.).
Notation:
- Use the symbol ≅ to denote congruence (e.g., triangle ABC ≅ triangle DEF).
Example: In triangles ABC and DEF, if angle A = angle D, angle B = angle E, angle C = angle F, and AB = DE, BC = EF, AC = DF, then triangle ABC ≅ triangle DEF.
Conditions for Congruency of Triangles
S.S.S. (Side-Side-Side)
If all three sides of one triangle equal the three sides of another triangle, the triangles are congruent.
Stepwise Explanation:
- Measure all three sides of both triangles.
- Compare each side of one triangle with the corresponding side of the other.
- If AB = DE, BC = EF, and AC = DF, the triangles are congruent by S.S.S.
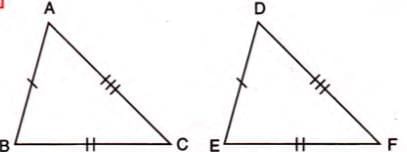
Example: In triangles ABC and DEF, if AB = DE, BC = EF, and AC = DF, then triangle ABC ≅ triangle DEF by S.S.S.
S.A.S. (Side-Angle-Side)
If two sides and the angle between them in one triangle equal two sides and the included angle in another, the triangles are congruent.
Stepwise Explanation:
- Identify two sides and the angle between them in both triangles.
- Ensure the angle/Support angle is between the two sides (included angle).
- If AB = DE, BC = EF, and angle B = angle E, the triangles are congruent by S.A.S.
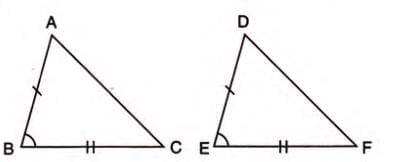
Example: In triangles ABC and DEF, if AB = DE, BC = EF, and angle B = angle E, then triangle ABC ≅ triangle DEF by S.A.S.
A.S.A. (Angle-Side-Angle)
If two angles and the side between them in one triangle equal two angles and the included side in another, the triangles are congruent.
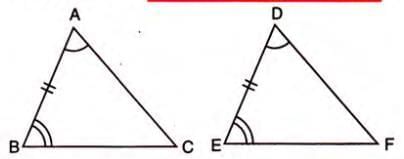
Stepwise Explanation:
- Identify two angles and the side between them in both triangles.
- Ensure the side is between the two angles (included side).
- If angle A = angle D, angle B = angle E, and AB = DE, the triangles are congruent by A.S.A.
Alternate Method (A.A.S.):
- If two angles and a non-included side of one triangle equal two angles and the corresponding non-included side of another, the triangles are congruent.
- This is equivalent to A.S.A. because the third angles are equal (sum of angles in a triangle is 180°).
Stepwise Explanation for A.A.S.:
- Check two angles and any side in both triangles.
- Since angle A = angle D and angle B = angle E, then angle C = angle F (by angle sum).
- If AC = DF, the triangles are congruent by A.S.A. (reordered).
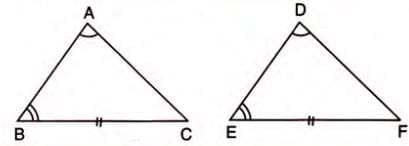
Example: In triangles ABC and DEF, if angle A = angle D, angle B = angle E, and AB = DE, then triangle ABC ≅ triangle DEF by A.S.A.
R.H.S. (Right Angle-Hypotenuse-Side)
If both triangles are right-angled, and their hypotenuses and one other side are equal, the triangles are congruent.
Stepwise Explanation:
- Identify the right angle in both triangles (e.g., angle B = angle E = 90°).
- Compare the hypotenuses (e.g., AC = DF).
- Compare one other side (e.g., AB = DE).
- If these match, the triangles are congruent by R.H.S.
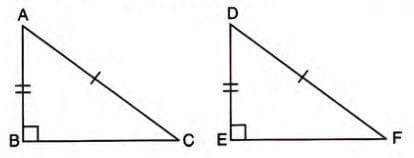
Example: In triangles ABC and DEF, if angle B = angle E = 90°, AC = DF (hypotenuses), and AB = DE, then triangle ABC ≅ triangle DEF by R.H.S.
Important Note on Congruence Notation
The order of vertices in the congruence statement must match corresponding vertices.
Stepwise Explanation:
- Identify corresponding angles (e.g., angle A = angle D, so A corresponds to D).
- Write the congruence statement ensuring corresponding vertices are in the same position (e.g., triangle ABC ≅ triangle DEF, not DFE).
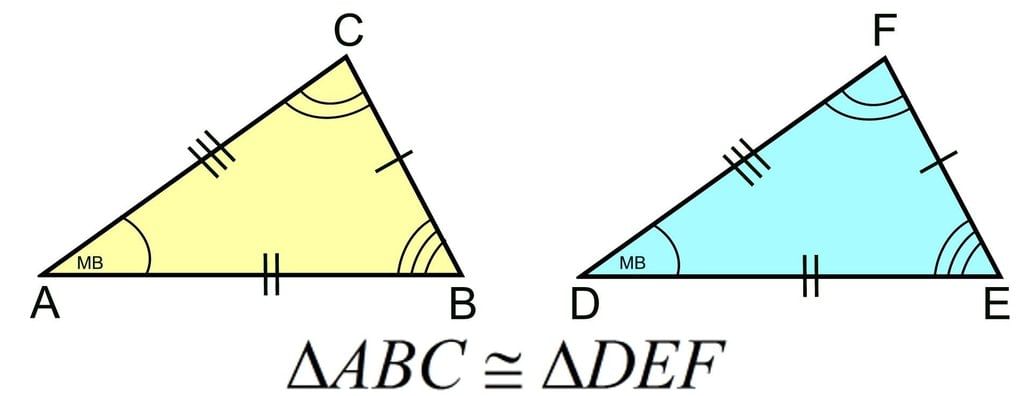
Example: If triangle ABC ≅ triangle DEF with angle A = angle D, angle B = angle E, angle C = angle F, then write triangle ABC ≅ triangle DEF, where A ↔ D, B ↔ E, C ↔ F.
|
64 videos|136 docs|28 tests
|
FAQs on Triangles Chapter Notes - Mathematics Class 9 ICSE
| 1. What is the relationship between the sides and angles of triangles? |  |
| 2. What are congruent triangles and how can they be identified? |  |
| 3. What are some important terms related to triangles? |  |
| 4. What are the conditions for the congruency of triangles? |  |
| 5. How can the knowledge of triangles be applied in real-life situations? |  |














