Class 9 Exam > Class 9 Notes > Mathematics Class 9 ICSE > Chapter Notes: Inequalities
Inequalities Chapter Notes | Mathematics Class 9 ICSE PDF Download
| Table of contents |
|
| Introduction |
|
| Theorem 3 |
|
| Theorem 4 (Converse of Theorem 3) |
|
| Theorem 5 |
|
| Corollary 1 |
|
| Corollary 2 |
|
Introduction
Inequalities are like the spice of geometry, adding a twist to how we compare lengths and angles in shapes, especially triangles and quadrilaterals. This chapter takes you on an exciting journey through the world of "greater than" and "less than," revealing secrets about sides and angles that make geometry feel like solving a puzzle. By understanding these concepts, you'll unlock the ability to compare distances and angles in a way that makes math both logical and fun!
- The symbol > means "is greater than." For example, if 'a' is larger than 'b', we write a > b.
- The symbol < means "is less than." For example, if 'a' is smaller than 'b', we write a < b.
Theorem 3
- Statement: If two sides of a triangle are unequal, the greater side has the greater angle opposite to it.
- Given: In triangle ABC, side AB is longer than side AC.
- To Prove: Angle ACB is greater than angle B.
- Construction: From side AB, cut off a segment AD equal to AC. Join points C and D.
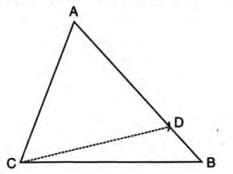
- Proof Steps:
- In triangle ACD, AC equals AD (by construction).
- Angles opposite equal sides are equal, so angle ACD equals angle ADC.
- In triangle BDC, the exterior angle ADC is greater than the interior opposite angle B.
- From the above, angle ACD is greater than angle B.
- Since angle ACD is part of angle ACB, angle ACB is greater than angle ACD, and thus angle ACB is greater than angle B.
Theorem 4 (Converse of Theorem 3)
- Statement: If two angles of a triangle are unequal, the greater angle has the greater side opposite to it.
- Given: In triangle ABC, angle CAB is greater than angle B.
- To Prove: Side BC is longer than side AC.
- Construction: Draw angle BAD equal to angle B.
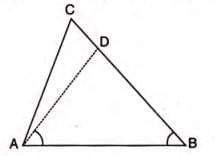
- Proof Steps:
- In triangle ABD, sides opposite equal angles (BAD and B) are equal, so AD equals BD.
- In triangle ADC, the sum of sides AD and DC is greater than side AC (triangle inequality).
- Since AD equals BD, BD plus DC (which is BC) is greater than AC.
- Thus, BC is greater than AC.
Theorem 5
- Statement: Of all lines drawn from a point outside a given straight line to that line, the perpendicular is the shortest.
- Given: Point O is outside line AB, and OP is perpendicular to AB.
- To Prove: OP is the shortest line from O to any point on AB.
- Construction: Join point O to any point Q on AB.
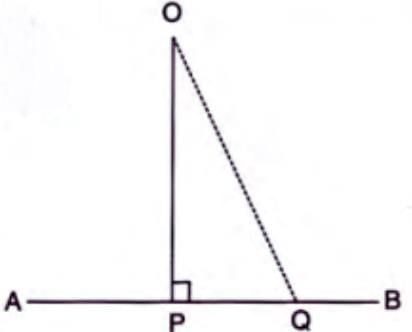
- Proof Steps:
- In right-angled triangle OPQ, angle OPQ (90°) is the greatest angle.
- The side opposite the greater angle (OQ) is greater than the side opposite the smaller angle (OP).
- Similarly, OP is shorter than any other line from O to AB.
- Thus, OP is the shortest line from O to AB.
Corollary 1
- Statement: The sum of any two sides of a triangle is always greater than the third side.
- Example:In triangle ABC:
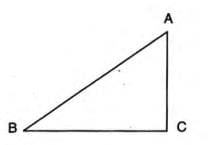
- AB + AC > BC
- AB + BC > AC
- BC + AC > AB
Corollary 2
- Statement: The difference between any two sides of a triangle is always less than the third side.
- Example:In triangle ABC, if AB is the largest side and AC is the smallest:
- AB - AC < BC
- AB - BC < AC
- BC - AC < AB
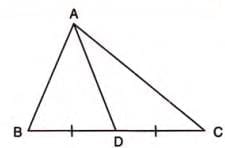
Example 1: In a figure, AD bisects angle A. Arrange AB, BD, and DC in descending order of their lengths.
Solution Steps: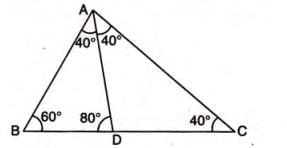
- Calculate angle BAC: 180° - (60° + 40°) = 80°.
- Since AD bisects angle A, angle BAD = angle CAD = 80°/2 = 40°.
- In triangle ABD, angle ADB = 180° - (60° + 40°) = 80°.
- In triangle ABD, side AB (opposite angle ADB, 80°) is greater than AD (opposite angle ABD, 60°), which is greater than BD (opposite angle BAD, 40°).
- In triangle ADC, sides AD and DC are equal (opposite equal angles CAD and ACD, both 40°).
- Thus, AB > DC = AD > BD.
- Answer: AB > DC > BD.
Example 2: In a figure, AC is perpendicular to line PQ, and BC = CD. Show that AE > AB.
Solution Steps:
- In triangles ABC and ADC: BC = CD (given), angle ACB = angle ACD (both 90°), AC is common.
- Triangles ABC and ADC are congruent by SAS (Side-Angle-Side).
- Thus, AB = AD and angle a (at A in ABC) = angle b (at A in ADC) by CPCTC (Corresponding Parts of Congruent Triangles are Congruent).
- In triangle ADC, exterior angle b = angle c + angle DAE.
- Thus, angle b > angle c.
- Since angle a = angle b, angle a > angle c.
- In triangle ABE, angle a > angle c, so side AE (opposite angle a) is greater than side AB (opposite angle c).
- Conclusion: AE > AB.
Example 3: Problem: In a figure, AB = AC. Prove that AF > AE.
Solution:
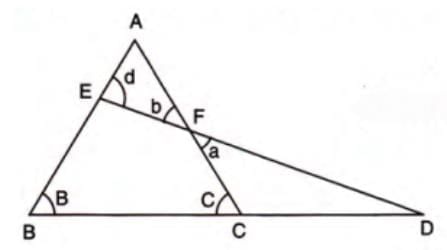
Steps:
- Since AB = AC, angles B and C are equal (angles opposite equal sides).
- In triangle FCD, exterior angle C = angle D + angle a.
- Thus, angle C > angle a.
- Since angle a = angle b (opposite equal sides FD and FE), angle C > angle b.
- In triangle EBD, exterior angle d = angle B + angle D.
- Thus, angle d > angle B, and since angle B = angle C, angle d > angle C.
- Combining, angle d > angle C > angle b, so angle d > angle b.
- In triangle AEF, angle d > angle b, so side AF (opposite angle d) is greater than side AE (opposite angle b).
- Conclusion: AF > AE.
Example 4: In a figure, AD bisects angle BAC. Prove that: (i) AB > BD, (ii) AC > CD, (iii) AB + AC > BC.
Solution:
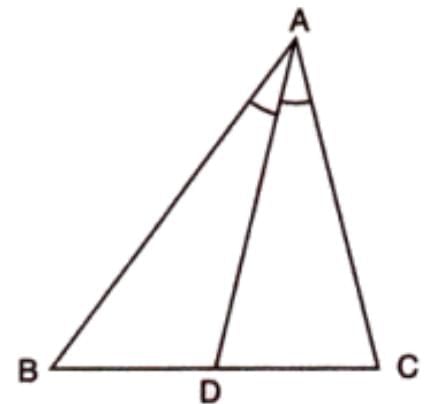
Steps:
Given: AD bisects angle BAC, so angle BAD = angle CAD.
(i) In triangle ADC, exterior angle ADB = angle CAD + angle C = angle BAD + angle C (since angle CAD = angle BAD).
- Thus, angle ADB > angle BAD.
- In triangle ABD, angle ADB > angle BAD, so side AB (opposite angle ADB) is greater than side BD (opposite angle BAD).
(ii) In triangle ABD, exterior angle ADC = angle BAD + angle B = angle CAD + angle B (since angle BAD = angle CAD).
- Thus, angle ADC > angle CAD.
- In triangle ADC, angle ADC > angle CAD, so side AC (opposite angle ADC) is greater than side CD (opposite angle CAD).
(iii) Since AB > BD and AC > CD, adding gives AB + AC > BD + CD.
- Since BD + CD = BC, AB + AC > BC.
Conclusion: (i) AB > BD, (ii) AC > CD, (iii) AB + AC > BC.
Example 5: In quadrilateral ABCD, AB is the shortest side and DC is the longest side. Prove that: (i) angle B > angle D, (ii) angle A > angle C.
Solution:
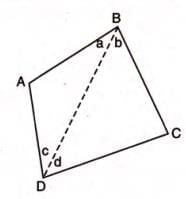
Steps:
- Join points B and D.
- In triangle ABD, side AD > AB (AB is shortest), so angle a (opposite AD) > angle c (opposite AB).
- In triangle BCD, side CD > BC (CD is longest), so angle b (opposite CD) > angle d (opposite BC).
- Adding: angle a + angle b > angle c + angle d.
- Since angle a + angle b = angle B and angle c + angle d = angle D, angle B > angle D.
- Similarly, join points A and C.
- By similar reasoning, angle A > angle C.
- Conclusion: (i) angle B > angle D, (ii) angle A > angle C.
Example 7: AD is a median of triangle ABC. Prove that AB + AC > 2 AD.
Solution:
- Given: AD is a median, so BD = CD.
- Extend AD to point E such that AD = DE, so AE = 2 AD.
- Join C and E.
- In triangle ACE, AC + CE > AE (sum of two sides greater than the third).
- Since AE = 2 AD, AC + CE > 2 AD.
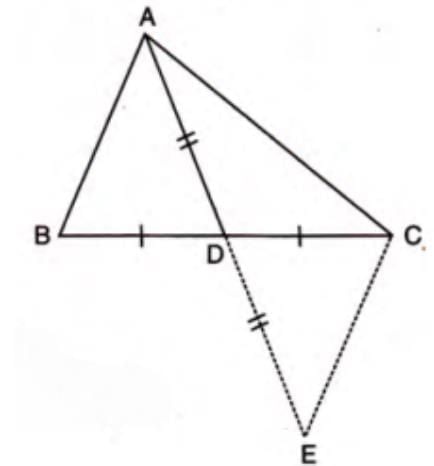
- In triangles ADB and CDE: BD = CD (given), AD = DE (by construction), angle ADB = angle CDE (vertically opposite).
- Triangles ADB and CDE are congruent by SAS.
- Thus, AB = CE by CPCTC.
- Substitute CE = AB in AC + CE > 2 AD to get AB + AC > 2 AD.
- Conclusion: AB + AC > 2 AD.
Example 6: In triangle ABC, BP is a median. Prove that PB + PA < BC + AC.
Solution:
Steps:
- Extend BP to meet AC at point M.
- In triangle BCM, BC + CM > BM (sum of two sides greater than the third).
- In triangle APM, AM + PM > AP.
- Add the inequalities: BC + CM + AM + PM > BM + AP.
- Since CM + AM = AC and BM - PM = BP, we get BC + AC > BP + AP.
- Thus, PB + PA < BC + AC.
- Conclusion: PB + PA < BC + AC.
The document Inequalities Chapter Notes | Mathematics Class 9 ICSE is a part of the Class 9 Course Mathematics Class 9 ICSE.
All you need of Class 9 at this link: Class 9
|
28 videos|171 docs|28 tests
|
FAQs on Inequalities Chapter Notes - Mathematics Class 9 ICSE
| 1. What are inequalities in mathematics and why are they important in Class 9? |  |
Ans. Inequalities are mathematical expressions that show the relationship between two values when they are not equal. They are important in Class 9 as they help students understand concepts of comparison, problem-solving, and are foundational for advanced topics such as algebra and calculus. Mastering inequalities allows students to solve real-world problems, such as determining ranges of values for given conditions.
| 2. What is Theorem 3 about in the context of inequalities? | |
Ans. Theorem 3 typically states a specific property or rule regarding inequalities, such as the transitive property, which asserts that if a > b and b > c, then a > c. This theorem is crucial in solving complex problems involving multiple inequalities and aids in the logical reasoning necessary for higher-level mathematics.
| 3. How does Theorem 4 serve as a converse to Theorem 3? | |
Ans. Theorem 4, being the converse of Theorem 3, addresses the reverse relationship of the inequalities presented in Theorem 3. For example, if Theorem 3 states a certain property holds under specific conditions, Theorem 4 would explore whether the reverse conditions also hold true, thus providing a deeper understanding of the relationships between the values.
| 4. What are the main takeaways from the corollaries related to inequalities? | |
Ans. Corollaries are derived from theorems and provide additional insights or simplified applications of those theorems. In the context of inequalities, Corollary 1 and Corollary 2 may present specific cases or applications of the main theorems, helping students to apply the concepts in various scenarios and solve problems efficiently. They emphasize the practical use of theorems in real-world contexts.
| 5. How can students effectively study inequalities to prepare for exams? | |
Ans. Students can prepare for inequalities by practicing a variety of problems, understanding the fundamental theorems and corollaries, and applying them to real-life situations. Group study sessions, utilizing visual aids like number lines, and solving past exam papers are also effective strategies. Additionally, seeking clarification on complex topics from teachers or tutors can enhance comprehension and retention.
About this Document
4.76/5
Rating
Sep 06, 2025
Last updated
Document Description: Chapter Notes: Inequalities for Class 9 2025 is part of Mathematics Class 9 ICSE preparation.
The notes and questions for Chapter Notes: Inequalities have been prepared according to the Class 9 exam syllabus. Information about Chapter Notes: Inequalities covers topics
like Introduction, Theorem 3, Theorem 4 (Converse of Theorem 3), Theorem 5, Corollary 1, Corollary 2 and Chapter Notes: Inequalities Example, for Class 9 2025 Exam. Find important definitions, questions, notes, meanings, examples, exercises and tests below for Chapter Notes: Inequalities.
Introduction of Chapter Notes: Inequalities in English is available as part of our Mathematics Class 9 ICSE
for Class 9 & Chapter Notes: Inequalities in Hindi for Mathematics Class 9 ICSE course.
Download more important topics related with notes, lectures and mock test series for Class 9
Exam by signing up for free. Class 9: Inequalities Chapter Notes | Mathematics Class 9 ICSE
Description
Full syllabus notes, lecture & questions for Inequalities Chapter Notes | Mathematics Class 9 ICSE - Class 9 | Plus excerises question with solution to help you revise complete syllabus for Mathematics Class 9 ICSE | Best notes, free PDF download
Information about Chapter Notes: Inequalities
In this doc you can find the meaning of Chapter Notes: Inequalities defined & explained in the simplest way possible. Besides explaining types of
Chapter Notes: Inequalities theory, EduRev gives you an ample number of questions to practice Chapter Notes: Inequalities tests, examples and also practice Class 9
tests
Related Searches
Extra Questions
,Previous Year Questions with Solutions
,ppt
,MCQs
,study material
,mock tests for examination
,Sample Paper
,shortcuts and tricks
,video lectures
,Objective type Questions
,Viva Questions
,Exam
,Important questions
,Free
,past year papers
,Inequalities Chapter Notes | Mathematics Class 9 ICSE
,practice quizzes
,Inequalities Chapter Notes | Mathematics Class 9 ICSE
,Semester Notes
,Inequalities Chapter Notes | Mathematics Class 9 ICSE
,Summary
;
Additional Information about Chapter Notes: Inequalities for Class 9 Preparation
Chapter Notes: Inequalities Free PDF Download
The Chapter Notes: Inequalities is an invaluable resource that delves deep into the core of the Class 9 exam.
These study notes are curated by experts and cover all the essential topics and concepts, making your preparation more efficient and effective.
With the help of these notes, you can grasp complex subjects quickly, revise important points easily,
and reinforce your understanding of key concepts. The study notes are presented in a concise and easy-to-understand manner,
allowing you to optimize your learning process. Whether you're looking for best-recommended books, sample papers, study material,
or toppers' notes, this PDF has got you covered. Download the Chapter Notes: Inequalities now and kickstart your journey towards success in the Class 9 exam.
Importance of Chapter Notes: Inequalities
The importance of Chapter Notes: Inequalities cannot be overstated, especially for Class 9 aspirants.
This document holds the key to success in the Class 9 exam.
It offers a detailed understanding of the concept, providing invaluable insights into the topic.
By knowing the concepts well in advance, students can plan their preparation effectively.
Utilize this indispensable guide for a well-rounded preparation and achieve your desired results.
Chapter Notes: Inequalities
Chapter Notes: Inequalities Notes offer in-depth insights into the specific topic to help you master it with ease.
This comprehensive document covers all aspects related to Chapter Notes: Inequalities.
It includes detailed information about the exam syllabus, recommended books, and study materials for a well-rounded preparation.
Practice papers and question papers enable you to assess your progress effectively.
Additionally, the paper analysis provides valuable tips for tackling the exam strategically.
Access to Toppers' notes gives you an edge in understanding complex concepts.
Whether you're a beginner or aiming for advanced proficiency, Chapter Notes: Inequalities Notes on EduRev are your ultimate resource for success.
Chapter Notes: Inequalities Class 9 Questions
The "Chapter Notes: Inequalities Class 9 Questions" guide is a valuable resource for all aspiring students preparing for the
Class 9 exam. It focuses on providing a wide range of practice questions to help students gauge
their understanding of the exam topics. These questions cover the entire syllabus, ensuring comprehensive preparation.
The guide includes previous years' question papers for students to familiarize themselves with the exam's format and difficulty level.
Additionally, it offers subject-specific question banks, allowing students to focus on weak areas and improve their performance.
Study Chapter Notes: Inequalities on the App
Students of Class 9 can study Chapter Notes: Inequalities alongwith tests & analysis from the EduRev app,
which will help them while preparing for their exam. Apart from the Chapter Notes: Inequalities,
students can also utilize the EduRev App for other study materials such as previous year question papers, syllabus, important questions, etc.
The EduRev App will make your learning easier as you can access it from anywhere you want.
The content of Chapter Notes: Inequalities is prepared as per the latest Class 9 syllabus.
|
© EduRev
|
Education Revolution
|
|
Signup on EduRev and stay on top of your study goals
10M+ students crushing their study goals daily