Class 2 Exam > Class 2 Notes > Mathematics for Class 2 (Joyful-Mathematics) > Mind Map: Playing with Lines (Orientation of a Line)
Mind Map: Playing with Lines (Orientation of a Line) | Mathematics for Class 2 (Joyful-Mathematics) PDF Download
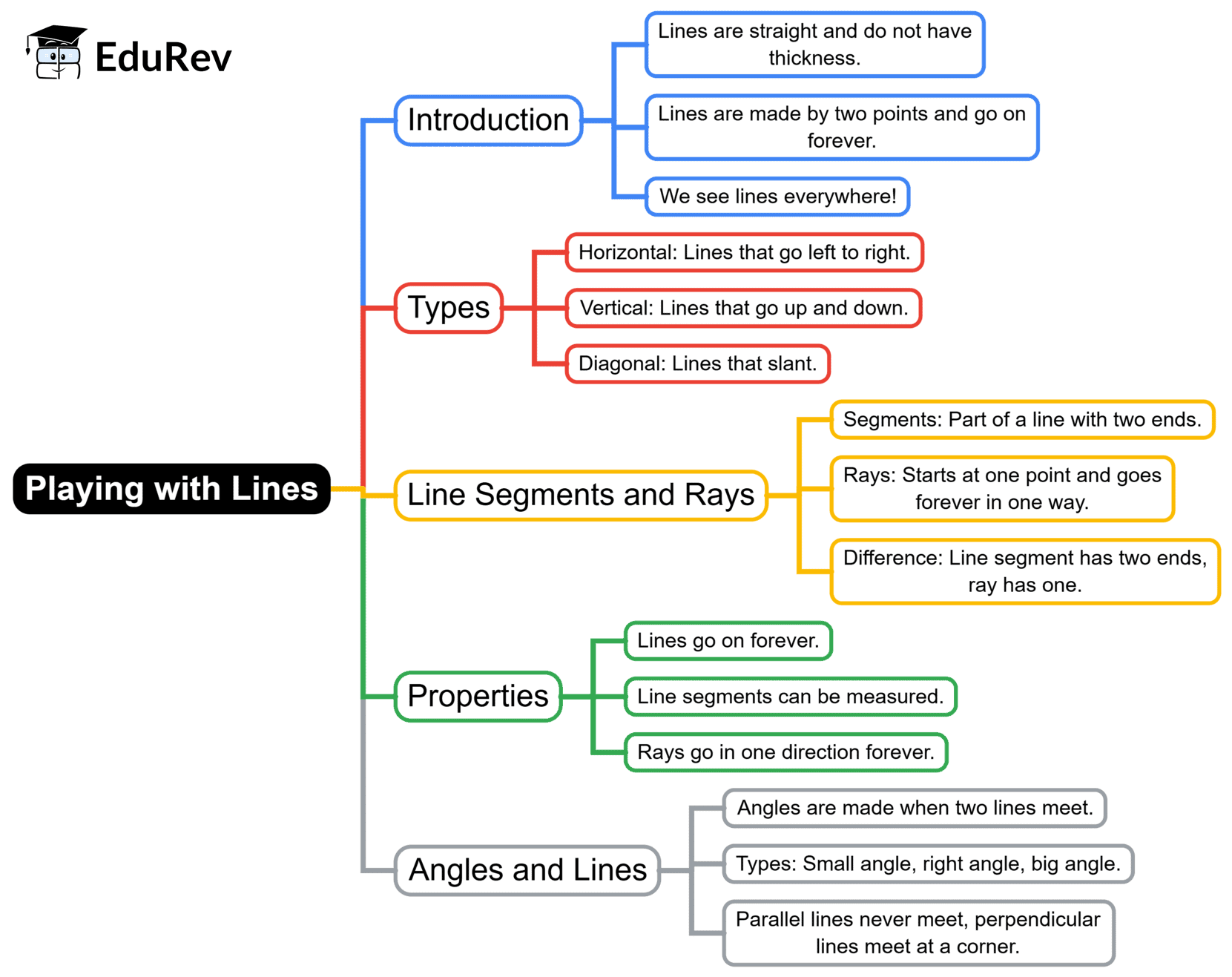
The document Mind Map: Playing with Lines (Orientation of a Line) | Mathematics for Class 2 (Joyful-Mathematics) is a part of the Class 2 Course Mathematics for Class 2 (Joyful-Mathematics).
All you need of Class 2 at this link: Class 2
|
28 videos|262 docs|22 tests
|
FAQs on Mind Map: Playing with Lines (Orientation of a Line) - Mathematics for Class 2 (Joyful-Mathematics)
| 1. What is the importance of understanding the orientation of a line in geometry? |  |
Ans.Understanding the orientation of a line is crucial in geometry as it helps in identifying the position and direction of the line in a coordinate system. It forms the basis for more complex concepts such as slopes, angles, and the relationships between different lines, which are essential for solving various geometric problems.
| 2. How can the orientation of a line be determined using its slope? | |
Ans.The orientation of a line can be determined by calculating its slope, which is the ratio of the change in the vertical direction (rise) to the change in the horizontal direction (run). A positive slope indicates the line rises from left to right, while a negative slope indicates it falls. A slope of zero represents a horizontal line, and an undefined slope indicates a vertical line.
| 3. What are the different types of lines based on their orientation? | |
Ans.Lines can be categorized based on their orientation into three main types: horizontal lines, vertical lines, and oblique (or inclined) lines. Horizontal lines run parallel to the x-axis, vertical lines run parallel to the y-axis, and oblique lines have a slope that is neither zero nor undefined, creating an angle with the axes.
| 4. How does the orientation of a line affect its equation in a coordinate plane? | |
Ans.The orientation of a line directly influences its equation in a coordinate plane. For example, the equation of a horizontal line is typically expressed as y = k, where k is a constant, while the equation of a vertical line is x = h, where h is a constant. Oblique lines have equations in the form y = mx + b, where m represents the slope and b is the y-intercept.
| 5. Can the orientation of a line change when graphed on different coordinate systems? | |
Ans.Yes, the orientation of a line can appear different when graphed on various coordinate systems, such as Cartesian, polar, or even in three-dimensional space. The fundamental relationships remain the same, but the representation may vary depending on the axes and the scale used in the specific coordinate system.
About this Document
4.92/5
Rating
Oct 04, 2025
Last updated
Related Exams
Document Description: Mind Map: Playing with Lines (Orientation of a Line) for Class 2 2025 is part of Mathematics for Class 2 (Joyful-Mathematics) preparation.
The notes and questions for Mind Map: Playing with Lines (Orientation of a Line) have been prepared according to the Class 2 exam syllabus. Information about Mind Map: Playing with Lines (Orientation of a Line) covers topics
like and Mind Map: Playing with Lines (Orientation of a Line) Example, for Class 2 2025 Exam. Find important definitions, questions, notes, meanings, examples, exercises and tests below for Mind Map: Playing with Lines (Orientation of a Line).
Introduction of Mind Map: Playing with Lines (Orientation of a Line) in English is available as part of our Mathematics for Class 2 (Joyful-Mathematics)
for Class 2 & Mind Map: Playing with Lines (Orientation of a Line) in Hindi for Mathematics for Class 2 (Joyful-Mathematics) course.
Download more important topics related with notes, lectures and mock test series for Class 2
Exam by signing up for free. Class 2: Mind Map: Playing with Lines (Orientation of a Line) | Mathematics for Class 2 (Joyful-Mathematics)
Description
Full syllabus notes, lecture & questions for Mind Map: Playing with Lines (Orientation of a Line) | Mathematics for Class 2 (Joyful-Mathematics) - Class 2 | Plus excerises question with solution to help you revise complete syllabus for Mathematics for Class 2 (Joyful-Mathematics) | Best notes, free PDF download
Information about Mind Map: Playing with Lines (Orientation of a Line)
In this doc you can find the meaning of Mind Map: Playing with Lines (Orientation of a Line) defined & explained in the simplest way possible. Besides explaining types of
Mind Map: Playing with Lines (Orientation of a Line) theory, EduRev gives you an ample number of questions to practice Mind Map: Playing with Lines (Orientation of a Line) tests, examples and also practice Class 2
tests
Related Searches
Exam
,Mind Map: Playing with Lines (Orientation of a Line) | Mathematics for Class 2 (Joyful-Mathematics)
,study material
,past year papers
,Free
,ppt
,Summary
,mock tests for examination
,Previous Year Questions with Solutions
,Mind Map: Playing with Lines (Orientation of a Line) | Mathematics for Class 2 (Joyful-Mathematics)
,Mind Map: Playing with Lines (Orientation of a Line) | Mathematics for Class 2 (Joyful-Mathematics)
,MCQs
,Extra Questions
,Objective type Questions
,video lectures
,Semester Notes
,Sample Paper
,practice quizzes
,Viva Questions
,Important questions
,shortcuts and tricks
;
Additional Information about Mind Map: Playing with Lines (Orientation of a Line) for Class 2 Preparation
Mind Map: Playing with Lines (Orientation of a Line) Free PDF Download
The Mind Map: Playing with Lines (Orientation of a Line) is an invaluable resource that delves deep into the core of the Class 2 exam.
These study notes are curated by experts and cover all the essential topics and concepts, making your preparation more efficient and effective.
With the help of these notes, you can grasp complex subjects quickly, revise important points easily,
and reinforce your understanding of key concepts. The study notes are presented in a concise and easy-to-understand manner,
allowing you to optimize your learning process. Whether you're looking for best-recommended books, sample papers, study material,
or toppers' notes, this PDF has got you covered. Download the Mind Map: Playing with Lines (Orientation of a Line) now and kickstart your journey towards success in the Class 2 exam.
Importance of Mind Map: Playing with Lines (Orientation of a Line)
The importance of Mind Map: Playing with Lines (Orientation of a Line) cannot be overstated, especially for Class 2 aspirants.
This document holds the key to success in the Class 2 exam.
It offers a detailed understanding of the concept, providing invaluable insights into the topic.
By knowing the concepts well in advance, students can plan their preparation effectively.
Utilize this indispensable guide for a well-rounded preparation and achieve your desired results.
Mind Map: Playing with Lines (Orientation of a Line) Notes
Mind Map: Playing with Lines (Orientation of a Line) Notes offer in-depth insights into the specific topic to help you master it with ease.
This comprehensive document covers all aspects related to Mind Map: Playing with Lines (Orientation of a Line).
It includes detailed information about the exam syllabus, recommended books, and study materials for a well-rounded preparation.
Practice papers and question papers enable you to assess your progress effectively.
Additionally, the paper analysis provides valuable tips for tackling the exam strategically.
Access to Toppers' notes gives you an edge in understanding complex concepts.
Whether you're a beginner or aiming for advanced proficiency, Mind Map: Playing with Lines (Orientation of a Line) Notes on EduRev are your ultimate resource for success.
Mind Map: Playing with Lines (Orientation of a Line) Class 2 Questions
The "Mind Map: Playing with Lines (Orientation of a Line) Class 2 Questions" guide is a valuable resource for all aspiring students preparing for the
Class 2 exam. It focuses on providing a wide range of practice questions to help students gauge
their understanding of the exam topics. These questions cover the entire syllabus, ensuring comprehensive preparation.
The guide includes previous years' question papers for students to familiarize themselves with the exam's format and difficulty level.
Additionally, it offers subject-specific question banks, allowing students to focus on weak areas and improve their performance.
Study Mind Map: Playing with Lines (Orientation of a Line) on the App
Students of Class 2 can study Mind Map: Playing with Lines (Orientation of a Line) alongwith tests & analysis from the EduRev app,
which will help them while preparing for their exam. Apart from the Mind Map: Playing with Lines (Orientation of a Line),
students can also utilize the EduRev App for other study materials such as previous year question papers, syllabus, important questions, etc.
The EduRev App will make your learning easier as you can access it from anywhere you want.
The content of Mind Map: Playing with Lines (Orientation of a Line) is prepared as per the latest Class 2 syllabus.
|
© EduRev
|
Education Revolution
|
|
Signup to see your scores
go up
within 7 days!
within 7 days!
Takes less than 10 seconds to signup