Pythagoras Theorem Chapter Notes | Mathematics Class 9 ICSE PDF Download
Introduction
Imagine a world where ancient mathematicians unlocked secrets of shapes that still guide architects, engineers, and scientists today! The Pythagoras Theorem, a gem from the treasure trove of mathematics, connects the sides of a right-angled triangle in a simple yet profound way. Named after the Greek mathematician Pythagoras, but with roots tracing back to the Indian mathematician Baudhayan, this theorem is a cornerstone of geometry. It helps us understand the relationship between the sides of a right-angled triangle and has practical applications in fields like construction, navigation, and even astronomy. Let’s dive into this fascinating chapter to explore its proofs, applications, and converse, making geometry both fun and meaningful!

- Baudhayan, an Indian mathematician (600 B.C.), discovered a relationship between the sides of a right-angled triangle.
- The theorem is named after Pythagoras, a Greek mathematician who gave it its modern form.
- It describes how the square of the hypotenuse (the longest side) relates to the squares of the other two sides in a right-angled triangle.
Pythagoras Theorem
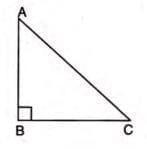
- Statement: In a right-angled triangle, the square of the hypotenuse equals the sum of the squares of the other two sides.
- Formula: For a right-angled triangle ABC with right angle at B, AC2 = AB2 + BC2.
Area-Based Proof Steps:
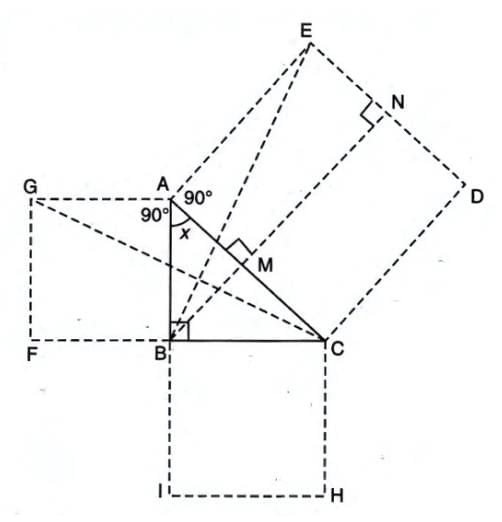
- Consider triangle ABC with ∠ABC = 90°.
- Construct squares on sides AC (ACDE), AB (ABFG), and BC (BCHI).
- Draw line BMN perpendicular to AC at M and DE at N, and join GC and BE.
- Prove ∠FBC = 180° (since ∠FBA = 90° and ∠ABC = 90°), making FBC a straight line.
- Show GA is parallel to FC (opposite sides of square ABFG).
- Show AE is parallel to BMN (both perpendicular to AC).
- Prove quadrilateral AMNE is a rectangle (all angles 90°).
- Let ∠BAC = x, then ∠GAC = ∠BAE (both 90° + x).
- Since AG = AB and AC = AE (sides of same square), triangle GAC is congruent to triangle BAE by SAS (Side-Angle-Side).
- Congruent triangles GAC and BAE have equal areas.
- Triangle GAC and square ABFG share base AG and are between parallels AG and CF, so area of triangle GAC = ½ × area of square ABFG.
- Similarly, triangle BAE and rectangle AMNE share base AE and are between parallels AE and BMN, so area of triangle BAE = ½ × area of rectangle AMNE.
- From above, area of square ABFG = area of rectangle AMNE.
- Similarly, prove area of square BCHI = area of rectangle CMND.
- Add areas: area of square ABFG + area of square BCHI = area of rectangle AMNE + area of rectangle CMND = area of square ACDE.
- Thus, AB2 + BC2 = AC2.
Converse of Pythagoras' Theorem: If the square of the largest side of a triangle equals the sum of the squares of the other two sides, the triangle is right-angled, with the right angle opposite the largest side.
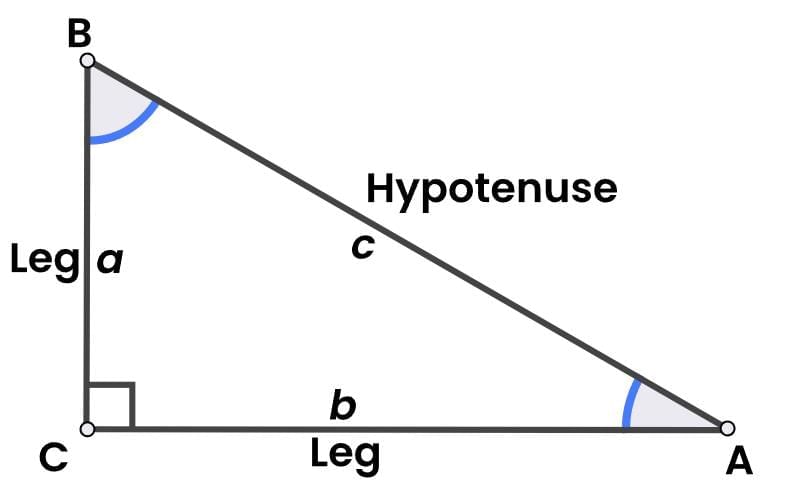
- Converse Formula: If AB is the largest side in triangle ABC and AB2 = AC2+ CB2, then ∠C = 90°.
Alternative Proof (Similarity-Based):
- Consider triangle ABC with ∠ABC = 90°.
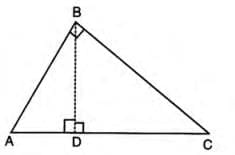
- Draw BD perpendicular to AC.
- In triangles ABC and BDC: ∠ABC = ∠BDC = 90°, ∠BCA = ∠BCD (common).
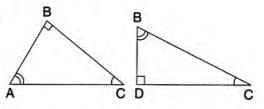
- By AA similarity, triangle ABC is similar to triangle BDC.
- Thus, BC/DC = AC/BC, so BC2 = AC × DC.
- In triangles ABC and ADB: ∠ABC = ∠ADB = 90°, ∠BAC = ∠BAD (common).
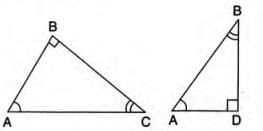
- By AA similarity, triangle ABC is similar to triangle ADB.
- Thus, AB/AD = AC/AB, so AB2 = AC × AD.
- Add equations: AB2 + BC2 = AC × AD + AC × DC = AC(AD + DC) = AC × AC = AC2.
Types of Triangles Based on Sides:
- If AB is the largest side and AB2 = AC2 + BC2, then ∠ACB = 90° (right-angled).
- If AB2 > AC2 + BC2, then ∠ACB > 90° (obtuse-angled).
- If AB2 < AC2 + BC2, then ∠ACB < 90° (acute-angled).
Notes:
- The hypotenuse is always the largest side in a right-angled triangle.
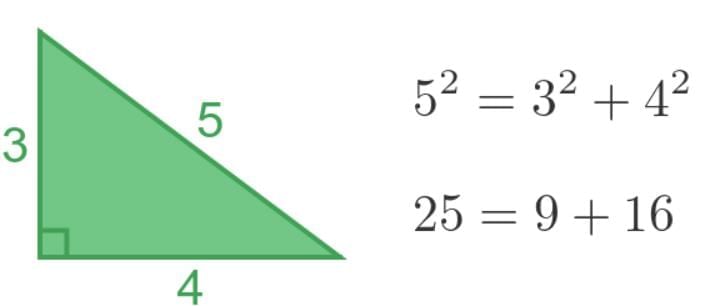
Pythagorean Triplets:
- Three positive numbers a, b, c (with c the largest) satisfying a2 + b2 = c2 are called Pythagorean triplets.
- Example: 3, 4, 5 (since 32 + 42 = 9 + 16 = 25 = 52).
Additional Proofs and Applications
Proof 1: Extended Pythagoras Theorem
Statement: In triangle ABC with AD perpendicular to BC produced, if AB = c, BC = a, AC = b, and BD = a + x, then c2 = a2 + b2 + 2ax.
Proof Steps:

- In right triangle ABD, apply Pythagoras Theorem: c2 = (a + x)2 + h2 (where h is AD).
- Expand: c2 = a2 + 2ax + x2 + h2.
- In right triangle ADC, x2 + h2 = b2.
- Substitute: c2 = a2 + (x2 + h2) + 2ax = a2 + b2 + 2ax.
Example: In triangle ABC, AD is perpendicular to BC produced. Prove c2 = a2 + b2 + 2ax.
Solution: In triangle ABD, c2 = (a + x)2 + h2 = a2 + 2ax + x2 + h2. In triangle ADC, x2 + h2 = b2. Thus, c2 = a2 + b2 + 2ax.
Proof 2: Right-Angled Triangle with Points on Sides
Statement: In triangle PQR, right-angled at Q, with M and N on QR and PQ, PM2 + RN2 = PR2 + MN2.
Proof Steps:
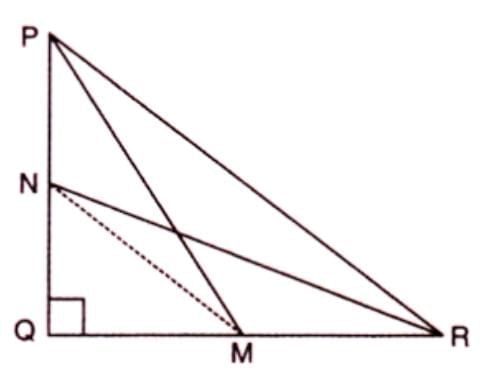
- In right triangle PQM, PM2 = PQ2 + QM2.
- In right triangle NQR, RN2 = NQ2 + QR2.
- Add: PM2 + RN2 = (PQ2 + QM2) + (NQ2 + QR2).
- Rearrange: (PQ2 + QR2) + (QM2 + NQ2).
- In triangle PQR, PR2 = PQ2 + QR2.
- In triangle MQN, MN2 = QM2 + NQ2.
- Thus, PM2 + RN2 = PR2 + MN2.
Example: In triangle PQR, right-angled at Q, M and N are points on QR and PQ. Prove PM2 + RN2 = PR2 + MN2.
Solution: Using Pythagoras Theorem in triangles PQM and NQR, sum their equations and substitute PR2 = PQ2 + QR2 and MN2 = QM2 + NQ2 to prove the result.
Proof 3: Perpendicular from Right Angle
Statement: In triangle ABC, ∠ACB = 90°, AB = c, BC = a, AC = b, CD perpendicular to AB, CD = p, then 1/p2 = 1/a2 + 1/b2.
Proof Steps:
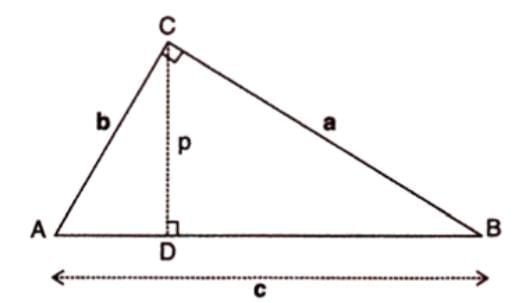
- In triangle ABC, c2 = b2 + a2.
- Area of triangle ABC = ½ × AB × CD = ½ × BC × AC.
- Thus, ½ × c × p = ½ × a × b, so c = ab/p.
- Substitute c in c2 = b2 + a2: (ab/p)2 = b2 + a2.
- Simplify: a2b2/p2 = b2 + a2.
- Divide by a2b2: 1/p2 = (b2 + a2)/(a2b2) = 1/a2 + 1/b2.
Example: In triangle ABC, ∠ACB = 90°, AB = c, BC = a, AC = b, CD perpendicular to AB, CD = p. Prove 1/p2 = 1/a2 + 1/b2.
Solution: Using area equality and Pythagoras Theorem, derive c = ab/p and substitute to prove 1/p2 = 1/a2 + 1/b2.
Proof 4: Equilateral Triangle with Point on Base
Statement: In equilateral triangle ABC, P is on BC with BP:PC = 2:1, then 9AP2 = 7AB2.
Proof Steps:
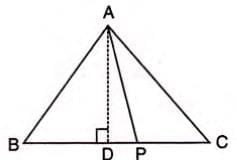
- Draw AD perpendicular to BC, so BD = CD = ½BC = ½AB.
- Given BP:PC = 2:1, so BP = (2/3)AB, PC = (1/3)AB.
- Calculate DP = BP - BD = (2/3)AB - (1/2)AB = AB/6.
- In right triangle ABD, AD2 = AB2 - BD2 = AB2 - (AB/2)2 = (3/4)AB2.
- In right triangle ADP, AP2 = AD2 + DP2 = (3/4)AB2 + (AB/6)2.
- Simplify: AP2 = (3/4)AB2 + (1/36)AB2 = (28/36)AB2 = (7/9)AB2.
- Thus, 9AP2 = 7AB2.
Example: In equilateral triangle ABC, P is on BC with BP:PC = 2:1. Prove 9AP2 = 7AB2.
Solution: Using perpendicular AD and given ratio, calculate DP and AD, then apply Pythagoras Theorem in triangle ADP to derive 9AP2 = 7AB2.
Proof 5: Isosceles Triangle with Perpendicular
Statement: In triangle ABC with AB > AC, E midpoint of BC, AD perpendicular to BC, then AB2 - AC2 = 2BC × ED.
Proof Steps:
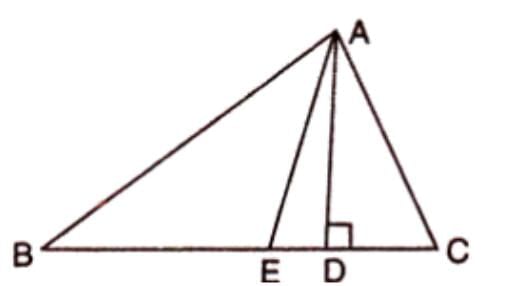
- In right triangle ABD, AB2 = AD2 + BD2.
- In right triangle ACD, AC2 = AD2 + CD2.
- Subtract: AB2 - AC2 = (AD2 + BD2) - (AD2 + CD2) = BD2 - CD2.
- Factorize: BD2 - CD2 = (BD + CD)(BD - CD) = BC(BD - CD).
- Since E is midpoint, BE = CE, so BD = BE + ED, CD = CE - ED.
- Thus, BD - CD = (BE + ED) - (CE - ED) = BE + ED - CE + ED = 2ED.
- Therefore, AB2 - AC2 = BC × 2ED = 2BC × ED.
Example: In triangle ABC, AB > AC, E is midpoint of BC, AD perpendicular to BC. Prove AB2 - AC2 = 2BC × ED.
Solution: Using Pythagoras Theorem in triangles ABD and ACD, derive BD2 - CD2 = 2BC × ED with E as midpoint.
Proof 6: Isosceles Triangle with Rectangle Inside
Statement: In isosceles triangle ABC with AB = AC = 20 cm, BC = 24 cm, and rectangle PQRS inside with PQ = SR = y cm, PS = QR = 2x cm, then y = 16 - (4x/3).
Proof Steps:
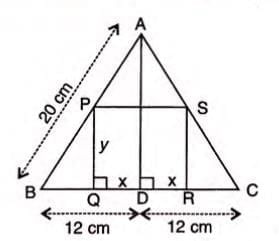
- In isosceles triangle, AD perpendicular to BC bisects BC, so BD = CD = 12 cm.
- By ASA congruence, triangles PBQ and SCR are congruent, so BQ = CR.
- Thus, DQ = DR = x cm, and BQ = CR = (12 - x) cm.
- In right triangle ABD, AD2 = 202 - 122 = 256, so AD = 16 cm.
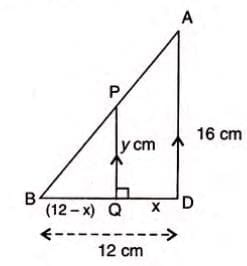
- Since PQ and AD are perpendicular to BD, PQ is parallel to AD.
- In triangle ABD, by similar triangles, PQ/AD = BQ/BD.
- Substitute: y/16 = (12 - x)/12, so y = 16 - (4x/3).
Proof 7: Parallelogram Diagonals
Statement: In parallelogram ABCD, AC2 + BD2 = AB2 + BC2 + CD2 + DA2.
Proof Steps:
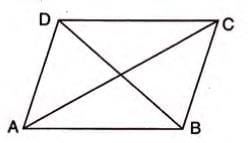
- Draw AN perpendicular to CD produced and DM perpendicular to AB.
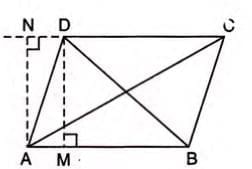
- In right triangle ANC, AC2 = AN2 + (CD + DN)2 = AN2 + CD2 + DN2 + 2CD × DN.
- Rearrange: AC2 = (AN2 + DN2) + CD2 + 2CD × DN = AD2 + CD2 + 2CD × DN.
- In right triangle DMB, BD2 = DM2 + (AB - AM)2 = DM2 + AB2 + AM2 - 2AB × AM.
- Since AB = CD and AM = DN (rectangle AMDN), BD2 = AD2 + AB2 - 2CD × DN.
- Add: AC2 + BD2 = (AD2 + CD2 + 2CD × DN) + (AD2 + AB2 - 2CD × DN).
- Simplify: = AB2 + BC2 + CD2 + DA2 (since AD = BC).
Special Cases:
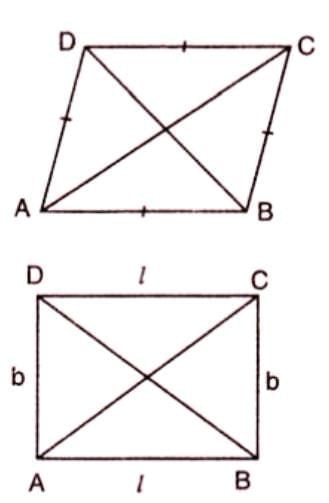
- In a rhombus: 4 × (side)2 = AC2 + BD2.
- In a rectangle: l2 + b2 = d2 (where l = length, b = breadth, d = diagonal).
|
64 videos|196 docs|28 tests
|
FAQs on Pythagoras Theorem Chapter Notes - Mathematics Class 9 ICSE
| 1. What is the Pythagorean Theorem and how is it expressed mathematically? |  |
| 2. How can the Pythagorean Theorem be applied in real-life situations? |  |
| 3. Are there any proofs of the Pythagorean Theorem besides the traditional one? |  |
| 4. In what ways can the Pythagorean Theorem be useful in mathematical problem-solving? |  |
| 5. What historical significance does the Pythagorean Theorem hold? |  |





















