Area Theorems Chapter Notes | Mathematics Class 9 ICSE PDF Download
Introduction
Ever wondered how to compare the areas of different shapes like triangles, parallelograms, and rectangles? The "Area Theorems (Proof and Use)" chapter from Class 9 ICSE Mathematics is your guide to unlocking these mysteries! This chapter dives into the fascinating world of geometry, where we explore how shapes with shared properties, like bases or heights, relate to each other in terms of area. By understanding these theorems, you'll know how to prove why certain shapes have equal areas under specific conditions
- The area of a shape is the space enclosed within its boundaries.
- Students are familiar with basic area formulas for common shapes.
- Area of a triangle = 1/2 × base × height
- Area of a rectangle = length × breadth
- Area of a parallelogram = base × height
- This chapter focuses on comparing areas of shapes like parallelograms, rectangles, and triangles under specific conditions.
- Equal figures refer to shapes with the same area.
- Congruent figures always have equal areas, but shapes with equal areas are not always congruent.
- Example: If a triangle has a base of 6 cm and a height of 4 cm, its area is calculated as:
Area = 1/2 × 6 × 4 = 12 cm2.
Figures Between the Same Parallels

- Shapes like parallelograms, rectangles, and triangles are said to be between the same parallels if their bases lie on one straight line (e.g., CD) and their opposite vertices lie on another parallel line (e.g., AB).
- Such shapes have equal heights (altitudes).
- If the bases of these shapes are equal in length, they are described as being on equal bases and between the same parallels.
- Example: In a figure, parallelogram PQRS, rectangle EFGH, and triangle LMN have their bases QR, FG, and MN on line CD, with vertices P, S, E, H, L, and M on line AB parallel to CD. If QR = FG = MN, these shapes are on equal bases and between the same parallels, sharing the same height.
Theorem 19: Parallelograms on the Same Base and Between the Same Parallels
Parallelograms sharing the same base and lying between the same parallel lines have equal areas.
Proof:
Given: Parallelograms ABCD and ABEF share base AB and lie between parallels AB and DE.
To Prove: Area of parallelogram ABCD = Area of parallelogram ABEF.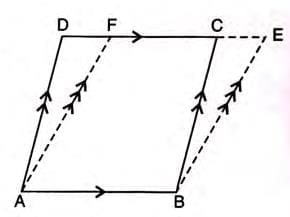 Proof Steps:
Proof Steps:
- In triangles ADF and BCE:
- AD = BC (opposite sides of parallelogram ABCD).
- ∠ADF = ∠BCE (corresponding angles).
- ∠AFD = ∠BEC (corresponding angles).
- ∠DAF = ∠CBE (since two angles are equal, the third angles are equal).
- Triangle ADF ≅ Triangle BCE (by ASA congruence).
- Area of triangle ADF = Area of triangle BCE (congruent triangles have equal areas).
- Add area of quadrilateral ABCF to both sides:
- Area of triangle ADF + Area of ABCF = Area of triangle BCE + Area of ABCF.
- Thus, Area of parallelogram ABCD = Area of parallelogram ABEF.
- Hence Proved.
- Corollary: A parallelogram and a rectangle on the same base and between the same parallels have equal areas.
- Example: Parallelograms ABCD and ABEF are on base AB and between parallels AB and DE. Since they share the same base and height, their areas are equal.
Theorem 20: Area of a Triangle and Parallelogram
The area of a triangle is half the area of a parallelogram on the same base and between the same parallels.
Proof:
Given: Triangle ABC and parallelogram ABDE share base AB and lie between parallels AB and ED.
To Prove: Area of triangle ABC = 1/2 × Area of parallelogram ABDE.
Construction: Complete parallelogram ABFC.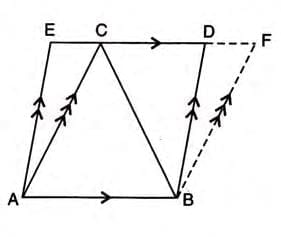 Proof Steps:
Proof Steps:
- BC is the diagonal of parallelogram ABFC.
- Area of triangle ABC = 1/2 × Area of parallelogram ABFC (diagonal divides a parallelogram into two equal triangles).
- Parallelograms ABFC and ABDE are on the same base AB and between the same parallels, so their areas are equal.
- Thus, Area of triangle ABC = 1/2 × Area of parallelogram ABDE.
- Hence Proved.
- Example: Triangle ABC and parallelogram ABDE are on base AB and between parallels AB and ED. If the parallelogram’s area is 100 cm2, the triangle’s area is 1/2 × 100 = 50 cm2.
Theorem 21: Triangles on the Same Base and Between the Same Parallels
Triangles sharing the same base and lying between the same parallel lines have equal areas.
Proof:
Given: Triangles ABC and ABD share base AB and lie between parallels AB and CD.
To Prove: Area of triangle ABC = Area of triangle ABD.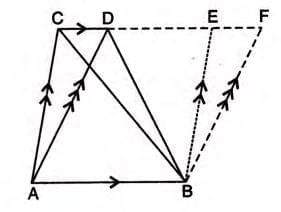 Construction: Complete parallelograms ABEC and ABFD.
Construction: Complete parallelograms ABEC and ABFD.
Proof Steps:
- BC is the diagonal of parallelogram ABEC, so Area of triangle ABC = 1/2 × Area of parallelogram ABEC.
- BD is the diagonal of parallelogram ABFD, so Area of triangle ABD = 1/2 × Area of parallelogram ABFD.
- Parallelograms ABEC and ABFD are on the same base AB and between the same parallels, so their areas are equal.
- Thus, Area of triangle ABC = Area of triangle ABD.
- Hence Proved.
Example: Triangles ABC and ABD are on base AB and between parallels AB and CD. Since they share the same base and height, their areas are equal.
Equal Areas and Corresponding Altitudes
- If two triangles have equal areas and share the same base (or equal bases), their corresponding altitudes are equal.
- Example: Triangles ABC and DBC are on the same base BC and have equal areas. Their altitudes AP (from A to BC) and DQ (from D to BC) are equal. Similarly, if triangles ABC and PQR have equal bases BC and QR and equal areas, their altitudes AD and PT are equal.
Proofs Involving Parallelograms and Triangles
Proof 1: Area of Parallelograms DEFH and ABCD
Given: AB || DC || EF, AD || BE, and DE || AF.
To Prove: Area of parallelogram DEFH = Area of parallelogram ABCD.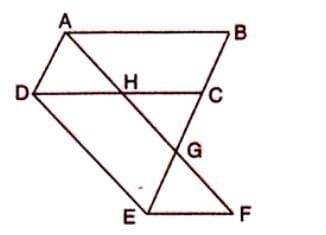 Proof Steps:
Proof Steps:
- Parallelograms DEFH and DEGA share base DE and lie between parallels DE and AF, so their areas are equal (Area of DEFH = Area of DEGA).
- Parallelograms ABCD and DEGA share base AD and lie between parallels AD and BE, so their areas are equal (Area of ABCD = Area of DEGA).
- From the above, Area of DEFH = Area of ABCD.
- Hence Proved.
Example: In a figure where AB || DC || EF, AD || BE, and DE || AF, parallelograms DEFH and ABCD are equal in area because they can be linked through intermediate parallelograms with equal areas.
Proof 2: Triangles Inside a Parallelogram
Given: P is a point inside parallelogram ABCD.
To Prove: Area of triangle APB + Area of triangle CPD = Area of triangle APD + Area of triangle BPC.
Construction: Draw RS through P parallel to AB, meeting AD at R and BC at S. Draw MN through P parallel to AD, meeting AB at N and CD at M.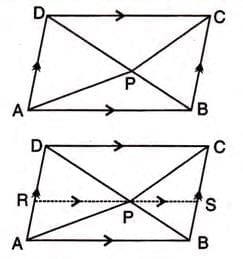 Proof Steps:
Proof Steps:
- Triangle APB and parallelogram ARSB share base AB and lie between parallels AB and RS, so Area of triangle APB = 1/2 × Area of parallelogram ARSB.
- Triangle CPD and parallelogram DRSC share base DC and lie between parallels DC and RS, so Area of triangle CPD = 1/2 × Area of parallelogram DRSC.
- Add the areas: Area of triangle APB + Area of triangle CPD = 1/2 × (Area of ARSB + Area of DRSC) = 1/2 × Area of parallelogram ABCD.
- Triangle APD and parallelogram ANMD share base AD and lie between parallels AD and MN, so Area of triangle APD = 1/2 × Area of parallelogram ANMD.
- Triangle BPC and parallelogram BNMC share base BC and lie between parallels BC and MN, so Area of triangle BPC = 1/2 × Area of parallelogram BNMC.
- Add the areas: Area of triangle APD + Area of triangle BPC = 1/2 × Area of parallelogram ABCD.
- Thus, Area of triangle APB + Area of triangle CPD = Area of triangle APD + Area of triangle BPC.
- Hence Proved.
Example: In parallelogram ABCD, point P is inside. Drawing lines through P parallel to AB and AD divides the parallelogram into smaller shapes, showing that the sum of areas of triangles APB and CPD equals the sum of areas of triangles APD and BPC.
Triangles with the Same Vertex and Bases Along the Same Line
- Triangles sharing the same vertex and having their bases along the same straight line have the same height.
- The areas of such triangles are in the ratio of their bases.
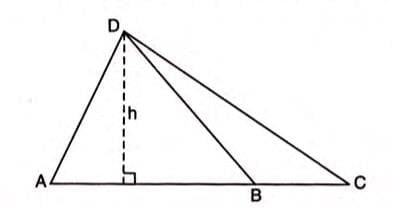
- Area of triangle ABD / Area of triangle BCD = AB / BC
- Area of triangle ABD / Area of triangle ACD = AB / AC
- Area of triangle BCD / Area of triangle ACD = BC / AC
- Example: In triangle ABC, D is a point on BC such that 2BD = 3DC. Thus, BD/DC = 3/2, and BD/BC = 3/5. Since triangles ABD and ABC share vertex A and have bases BD and BC along line BC, their areas are in the ratio BD/BC. Therefore, Area of triangle ABD = 3/5 × Area of triangle ABC.
Proofs Involving Triangles and Parallelograms
Proof 1: Median Divides a Triangle
To Prove: Area of triangle ABD = Area of triangle ADC = 1/2 × Area of triangle ABC.
Construction: Draw AP perpendicular to BC.
Proof Steps:
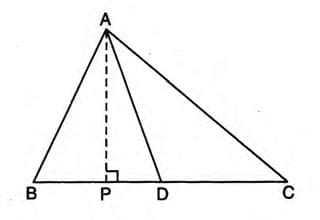
- Area of triangle ABD = 1/2 × BD × AP.
- Area of triangle ADC = 1/2 × DC × AP.
- Since D is the midpoint, BD = DC.
- Thus, Area of triangle ABD = Area of triangle ADC.
- Area of triangle ABC = Area of triangle ABD + Area of triangle ADC = 2 × Area of triangle ABD.
- Therefore, Area of triangle ABD = Area of triangle ADC = 1/2 × Area of triangle ABC.
- Hence Proved.
- Example: In triangle ABC, AD is a median. Drawing AP perpendicular to BC, the areas of triangles ABD and ADC are equal because BD = DC, and each is half the area of triangle ABC.
Proof 2: Ratio of Areas with a Point Dividing the Base
Given: In triangle ABC, D divides BC in the ratio m:n, so BD/DC = m/n.
To Prove: Area of triangle ABD / Area of triangle ADC = m/n.
Construction: Draw AP perpendicular to BC.
Proof Steps: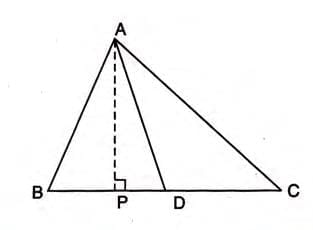
- Area of triangle ABD = 1/2 × BD × AP.
- Area of triangle ADC = 1/2 × DC × AP.
- Area of triangle ABD / Area of triangle ADC = (1/2 × BD × AP) / (1/2 × DC × AP) = BD/DC.
- Since BD/DC = m/n, Area of triangle ABD / Area of triangle ADC = m/n.
- Hence Proved.
Example: In triangle ABC, D divides BC such that BD/DC = 3/2. Drawing AP perpendicular to BC, the areas of triangles ABD and ADC are in the ratio BD/DC = 3/2.
Proof 3: Triangles with Points Trisecting a Side
Given: In parallelogram ABCD, points P and Q trisect side BC (BP = PQ = QC).
To Prove: Area of triangle APQ = Area of triangle DPQ = 1/6 × Area of parallelogram ABCD.
Proof Steps: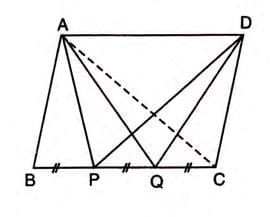
- Since BP = PQ = QC, BP/BC = 1/3 (bases of triangles ABP and ABC are in ratio 1:3).
- Triangles ABP and ABC share vertex A and have bases along BC, so Area of triangle ABP / Area of triangle ABC = BP/BC = 1/3.
- Thus, Area of triangle ABP = 1/3 × Area of triangle ABC.
- Diagonal AC bisects parallelogram ABCD, so Area of triangle ABC = 1/2 × Area of parallelogram ABCD.
- Therefore, Area of triangle ABP = 1/3 × 1/2 × Area of parallelogram ABCD = 1/6 × Area of parallelogram ABCD.
- Triangles ABP, APQ, and DPQ share equal bases (BP, PQ, QC) and lie between the same parallels, so their areas are equal.
- Thus, Area of triangle APQ = Area of triangle DPQ = 1/6 × Area of parallelogram ABCD.
- Hence Proved.
Example: In parallelogram ABCD, points P and Q trisect BC. The areas of triangles APQ and DPQ are each 1/6 of the parallelogram’s area because they share equal bases and the same height.
Proof 4: Triangles with Diagonals in a Quadrilateral
Given: Quadrilateral ABCD with diagonals AC and BD intersecting at O.
To Prove: Area of triangle AOD × Area of triangle BOC = Area of triangle AOB × Area of triangle COD.
Proof Steps: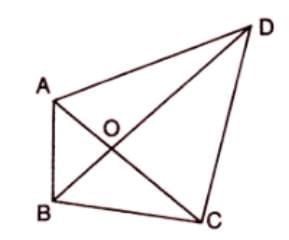
- Triangles AOB and AOD share vertex O and have bases AB and AD along line AD.
- Area of triangle AOB / Area of triangle AOD = BO/DO.
- Triangles BOC and COD share vertex O and have bases BC and CD along line BC.
- Area of triangle BOC / Area of triangle COD = BO/DO.
- Thus, Area of triangle AOB / Area of triangle AOD = Area of triangle BOC / Area of triangle COD.
- Therefore, Area of triangle AOD × Area of triangle BOC = Area of triangle AOB × Area of triangle COD.
- Hence Proved.
Example: In quadrilateral ABCD, diagonals AC and BD intersect at O. The product of the areas of triangles AOD and BOC equals the product of the areas of triangles AOB and COD because the ratios of their areas are equal based on their bases.
|
28 videos|171 docs|28 tests
|
FAQs on Area Theorems Chapter Notes - Mathematics Class 9 ICSE
| 1. What are the properties of figures between the same parallels? |  |
| 2. How do you calculate the area of triangles with the same vertex and bases along the same line? |  |
| 3. Can you explain the relationship between the area of two triangles with the same height? |  |
| 4. What is the significance of the area theorems in geometry? |  |
| 5. How do area theorems apply to real-world situations? |  |
















