Class 9 Exam > Class 9 Notes > Mathematics Class 9 ICSE > Chapter Notes: Solids
Solids Chapter Notes | Mathematics Class 9 ICSE PDF Download
| Table of contents |
|
| Introduction |
|
| Cuboid |
|
| Cube |
|
| Cost of an Article |
|
| Cross-Section |
|
| Flow of Water (Or Any Other Liquid) |
|
| Solved Examples |
|
Introduction
Imagine building a model castle or designing a storage box—how much space does it take up, and how much material do you need to cover it? Welcome to the fascinating world of 3-D solids! In this chapter, we dive into the concepts of volume and surface area for shapes like cuboids and cubes. We'll explore how to calculate the space they occupy and the area of their surfaces, which is super useful in real-life scenarios like construction, packaging, or even planning a water tank. Get ready to unravel the math behind three-dimensional objects in a simple and engaging way!
Solid: A solid is any object that takes up space and has a definite shape.
Volume refers to the amount of space a solid occupies.
- The capacity of a container is its internal volume.
- For hollow objects, the volume of material is found by subtracting the internal volume from the external volume.
Surface area is the total area of all the surfaces of a solid.
- Solids are three-dimensional (3-D) because they have length, breadth, and height.
- In contrast, an area (like a rectangle) is two-dimensional (2-D) with only length and breadth.
- A perimeter is one-dimensional (1-D) as it only involves length.
Cuboid
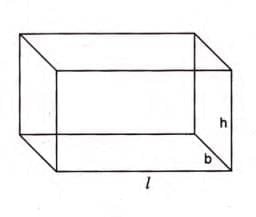
- A cuboid is a rectangular solid with six faces, each being a rectangle.
- Formulas for a cuboid(length = l, breadth = b, height = h):
- Volume = l × b × h
- Total surface area = 2(l × b + b × h + h × l)
- Lateral surface area = 2(l + b) × h
- Length of diagonal = √(l2 + b2 + h2)
- The diagonal of a cuboid is the longest rod that can fit inside it.
- Every cuboid has four equal diagonals (e.g., AG, BH, CE, DF in a cuboid).
Example:
A closed wooden box has outer dimensions of 22 cm, 15 cm, and 10 cm, with a wood thickness of 1 cm. The volume of wood is calculated as the difference between external and internal volumes.
- External volume = 22 × 15 × 10 = 3300 cm3.
- Internal dimensions = (22 - 2 × 1), (15 - 2 × 1), (10 - 2 × 1) = 20 cm, 13 cm, 8 cm.
- Internal volume = 20 × 13 × 8 = 2080 cm3.
- Volume of wood = 3300 - 2080 = 1220 cm3.
Example:
A small indoor greenhouse (a cuboid) has dimensions 40 cm × 30 cm × 25 cm, made entirely of glass panes.
- Area of glass (total surface area) = 2(40 × 30 + 30 × 25 + 25 × 40) = 2(1200 + 750 + 1000) = 5900 cm2.
- Tape length = Perimeter of top + Perimeter of bottom + Four vertical edges = 4(40 + 30) + 4 × 25 = 380 cm.
Cube
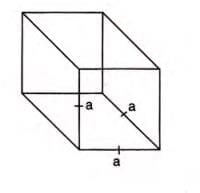
- A cube is a special cuboid where all six faces are squares of equal size.
- If the edge of a cube is 'a', then length = breadth = height = a.
- Formulas for a cube:
- Volume = a × a × a = a3
- Total surface area = 6a2
- Lateral surface area = 4a2
- Length of diagonal = √(a2 + a2 + a2) = a√3
Example:
A cube of metal with a 5 cm edge is melted and recast into a cuboid with a base of 2.5 cm × 0.5 cm.
- Volume of cube = 5 × 5 × 5 = 125 cm3.
- Volume of cuboid = 2.5 × 0.5 × h = 125.
- Height (h) = 125 / (2.5 × 0.5) = 100 cm.
- Surface area of cube = 6 × 52 = 150 cm2.
- Surface area of cuboid = 2(2.5 × 0.5 + 0.5 × 100 + 100 × 2.5) = 602.5 cm2.
Cost of an Article
- The cost of an article is calculated by multiplying its quantity by its rate.
- Formula: Cost = Rate × Quantity
- Examples of cost calculation:
- Petrol is bought by volume: Cost = Volume of petrol × Rate per unit volume.
- Land is bought by area: Cost = Area of land × Rate per unit area.
- Cloth is bought by length: Cost = Length of cloth × Rate per unit length.
Example:
A solid cubical block of wood costs ₹250 per m3, and a block is bought for ₹182.25.
- Volume = Cost / Rate = 182.25 / 250 = 0.729 m3.
- Edge of cube = (0.729)1/3 = (729/1000)1/3 = 0.9 m (using factors: 729 = 33 × 33, 1000 = 103).
Cross-Section
A cross-section is a cut made through a solid perpendicular to its length or height.
A solid has a uniform cross-sectionif the shape and size of the cross-section are the same at every point along its length or height.
- Example: A cuboid or right-circular cylinder has a uniform cross-section.
- A right-circular cone does not have a uniform cross-section because the size of the cross-section changes.
Formulas for solids with uniform cross-section:
- Volume = Area of cross-section × Length
- Surface area (excluding cross-section) = Perimeter of cross-section × Length
Example:
A solid with a trapezium cross-section has parallel sides 23 cm and 17 cm, height 10 cm, and length 1 m.
- Area of cross-section = (1/2) × (23 + 17) × 10 = 200 cm2.
- Volume = 200 × 100 = 20,000 cm3 (length = 1 m = 100 cm).
Flow of Water (Or Any Other Liquid)
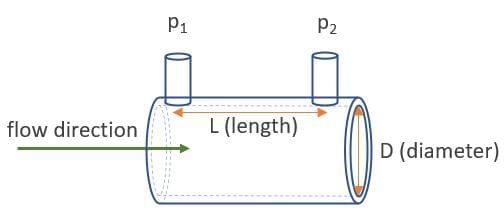
Water Flow Rate
- For a pipe or canal with a uniform cross-section, the volume of liquid flowing per unit time is calculated.
- Formula: Volume per unit time = Area of cross-section × Speed of flow
Example:
A pipe with a cross-sectional area of 5 cm2 has water flowing at 30 cm/s. Find the volume of water flowing in 1 minute.
- Volume per second = 5 × 30 = 150 cm3.
- Volume per minute = 150 × 60 = 9000 cm3 = 9 liters (since 1 liter = 1000 cm3).
Solved Examples
Example 1: Volume and Cost of Wood in a Box
A closed wooden box has outer dimensions 22 cm × 15 cm × 10 cm, with wood thickness 1 cm. Find the cost of wood at ₹7.50 per cm3.
- External volume = 22 × 15 × 10 = 3300 cm3.
- Internal dimensions = (22 - 2 × 1), (15 - 2 × 1), (10 - 2 × 1) = 20 cm, 13 cm, 8 cm.
- Internal volume = 20 × 13 × 8 = 2080 cm3.
- Volume of wood = 3300 - 2080 = 1220 cm3.
- Cost = 1220 × 7.50 = ₹9150.
Example 2: Cuboid from Melted Cube
A cube with a 5 cm edge is melted and recast into a cuboid with base 2.5 cm × 0.5 cm. Find the height and surface areas.
- Volume of cube = 53 = 125 cm3.
- Volume of cuboid = 2.5 × 0.5 × h = 125.
- Height (h) = 125 / (2.5 × 0.5) = 100 cm.
- Surface area of cube = 6 × 52 = 150 cm2.
- Surface area of cuboid = 2(2.5 × 0.5 + 0.5 × 100 + 100 × 2.5) = 602.5 cm2.
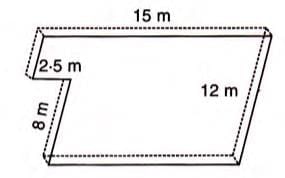
Example 3: Rise in Field Level
A field is 15 m × 12 m. A well of 8 m × 2.5 m × 2 m is dug, and the soil is spread over the remaining field. Find the rise in level.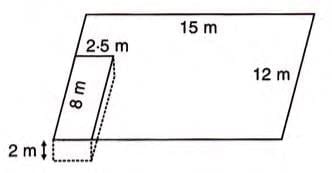
- Volume of soil = 8 × 2.5 × 2 = 40 m3.
- Area of remaining field = (15 × 12 - 8 × 2.5) = 160 m2.
- Rise in level (h) = Volume / Area = 40 / 160 = 0.25 m = 25 cm.
Example 4: Surface Area Using Diagonal
A cuboid has l + b + h = 19 cm and diagonal = 11 cm. Find its surface area.
- Given: l + b + h = 19, and √(l2 + b2 + h2) = 11, so l2 + b2 + h2 = 121.
- (l + b + h)2 = l2 + b2 + h2 + 2(lb + bh + hl).
- 192 = 121 + 2(lb + bh + hl) → 361 = 121 + 2(lb + bh + hl).
- 2(lb + bh + hl) = 361 - 121 = 240 cm2.
- Surface area = 240 cm2.
The document Solids Chapter Notes | Mathematics Class 9 ICSE is a part of the Class 9 Course Mathematics Class 9 ICSE.
All you need of Class 9 at this link: Class 9
|
28 videos|171 docs|28 tests
|
FAQs on Solids Chapter Notes - Mathematics Class 9 ICSE
| 1. What is a cuboid and how is it different from a cube? |  |
Ans. A cuboid is a three-dimensional geometric shape with six rectangular faces, while a cube is a special type of cuboid where all six faces are squares. In a cuboid, the length, width, and height can be different, whereas in a cube, all sides are equal in length.
| 2. How do you calculate the volume of a cube and a cuboid? | |
Ans. The volume of a cube is calculated by raising the length of one side to the power of three (Volume = side x side x side). For a cuboid, the volume is calculated by multiplying its length, width, and height (Volume = length x width x height).
| 3. What is the significance of the cross-section in solids? | |
Ans. The cross-section of a solid is the shape that is obtained when the solid is cut through a plane. It helps in visualizing and understanding the internal structure of the solid, which is important in various fields such as architecture, engineering, and biology.
| 4. How does the flow of water in a cuboidal tank differ from that in a cylindrical tank? | |
Ans. The flow of water in a cuboidal tank can be influenced by the shape and dimensions of the tank, affecting the surface area and volume. In a cylindrical tank, the water flow can be more uniform due to the circular cross-section. The differences in shapes can lead to variations in water pressure and flow rates.
| 5. How can the cost of an article be determined using its dimensions? | |
Ans. The cost of an article can be determined by calculating its volume or surface area, which can then be multiplied by the cost per unit volume or area. For example, if the article is made from a specific material priced per cubic unit, knowing its dimensions allows for accurate cost estimation based on the material's volume.
About this Document
Sep 07, 2025
Last updated
Related Exams
Document Description: Chapter Notes: Solids for Class 9 2025 is part of Mathematics Class 9 ICSE preparation.
The notes and questions for Chapter Notes: Solids have been prepared according to the Class 9 exam syllabus. Information about Chapter Notes: Solids covers topics
like Introduction, Cuboid, Cube, Cost of an Article, Cross-Section, Flow of Water (Or Any Other Liquid), Solved Examples and Chapter Notes: Solids Example, for Class 9 2025 Exam. Find important definitions, questions, notes, meanings, examples, exercises and tests below for Chapter Notes: Solids.
Introduction of Chapter Notes: Solids in English is available as part of our Mathematics Class 9 ICSE
for Class 9 & Chapter Notes: Solids in Hindi for Mathematics Class 9 ICSE course.
Download more important topics related with notes, lectures and mock test series for Class 9
Exam by signing up for free. Class 9: Solids Chapter Notes | Mathematics Class 9 ICSE
Description
Full syllabus notes, lecture & questions for Solids Chapter Notes | Mathematics Class 9 ICSE - Class 9 | Plus excerises question with solution to help you revise complete syllabus for Mathematics Class 9 ICSE | Best notes, free PDF download
Information about Chapter Notes: Solids
In this doc you can find the meaning of Chapter Notes: Solids defined & explained in the simplest way possible. Besides explaining types of
Chapter Notes: Solids theory, EduRev gives you an ample number of questions to practice Chapter Notes: Solids tests, examples and also practice Class 9
tests
Related Searches
Previous Year Questions with Solutions
,practice quizzes
,ppt
,MCQs
,Solids Chapter Notes | Mathematics Class 9 ICSE
,Sample Paper
,study material
,mock tests for examination
,past year papers
,Exam
,Free
,Solids Chapter Notes | Mathematics Class 9 ICSE
,Viva Questions
,Objective type Questions
,Important questions
,Summary
,Extra Questions
,Solids Chapter Notes | Mathematics Class 9 ICSE
,video lectures
,Semester Notes
,shortcuts and tricks
;
Additional Information about Chapter Notes: Solids for Class 9 Preparation
Chapter Notes: Solids Free PDF Download
The Chapter Notes: Solids is an invaluable resource that delves deep into the core of the Class 9 exam.
These study notes are curated by experts and cover all the essential topics and concepts, making your preparation more efficient and effective.
With the help of these notes, you can grasp complex subjects quickly, revise important points easily,
and reinforce your understanding of key concepts. The study notes are presented in a concise and easy-to-understand manner,
allowing you to optimize your learning process. Whether you're looking for best-recommended books, sample papers, study material,
or toppers' notes, this PDF has got you covered. Download the Chapter Notes: Solids now and kickstart your journey towards success in the Class 9 exam.
Importance of Chapter Notes: Solids
The importance of Chapter Notes: Solids cannot be overstated, especially for Class 9 aspirants.
This document holds the key to success in the Class 9 exam.
It offers a detailed understanding of the concept, providing invaluable insights into the topic.
By knowing the concepts well in advance, students can plan their preparation effectively.
Utilize this indispensable guide for a well-rounded preparation and achieve your desired results.
Chapter Notes: Solids
Chapter Notes: Solids Notes offer in-depth insights into the specific topic to help you master it with ease.
This comprehensive document covers all aspects related to Chapter Notes: Solids.
It includes detailed information about the exam syllabus, recommended books, and study materials for a well-rounded preparation.
Practice papers and question papers enable you to assess your progress effectively.
Additionally, the paper analysis provides valuable tips for tackling the exam strategically.
Access to Toppers' notes gives you an edge in understanding complex concepts.
Whether you're a beginner or aiming for advanced proficiency, Chapter Notes: Solids Notes on EduRev are your ultimate resource for success.
Chapter Notes: Solids Class 9 Questions
The "Chapter Notes: Solids Class 9 Questions" guide is a valuable resource for all aspiring students preparing for the
Class 9 exam. It focuses on providing a wide range of practice questions to help students gauge
their understanding of the exam topics. These questions cover the entire syllabus, ensuring comprehensive preparation.
The guide includes previous years' question papers for students to familiarize themselves with the exam's format and difficulty level.
Additionally, it offers subject-specific question banks, allowing students to focus on weak areas and improve their performance.
Study Chapter Notes: Solids on the App
Students of Class 9 can study Chapter Notes: Solids alongwith tests & analysis from the EduRev app,
which will help them while preparing for their exam. Apart from the Chapter Notes: Solids,
students can also utilize the EduRev App for other study materials such as previous year question papers, syllabus, important questions, etc.
The EduRev App will make your learning easier as you can access it from anywhere you want.
The content of Chapter Notes: Solids is prepared as per the latest Class 9 syllabus.
|
© EduRev
|
Education Revolution
|
|
Signup to see your scores
go up within 7 days!
Access 1000+ FREE Docs, Videos and Tests
Takes less than 10 seconds to signup