Class 9 Exam > Class 9 Notes > Mathematics Class 9 ICSE > Chapter Notes: Solution of Right Triangles
Solution of Right Triangles Chapter Notes | Mathematics Class 9 ICSE PDF Download
| Table of contents |
|
| Introduction |
|
| Solving When One Side and One Acute Angle Are Given |
|
| Solving When Two Sides Are Given |
|
| Applications in Geometric Figures |
|
| Real-World Applications |
|
| Solved Examples |
|
Introduction
Welcome to the fascinating world of right-angled triangles! In this chapter, we dive into solving problems related to right-angled triangles, a cornerstone of geometry that connects angles and sides in exciting ways. Whether you're finding missing sides or angles, this chapter equips you with the tools to tackle 2D problems with confidence. Using trigonometric ratios like sine, cosine, and tangent, you'll learn to unravel the mysteries of triangles with ease. Get ready to explore practical applications, from calculating heights to measuring distances, all through the lens of right-angled triangles!
Solving a right-angled triangle means finding the unknown sides and angles.
This is done when:
- One side and one acute angle are given.
- Two sides of the triangle are given.
Trigonometric ratios (sine, cosine, tangent) are used to relate angles and sides.
Key formulas:
- sin θ = Perpendicular / Hypotenuse
- cos θ = Base / Hypotenuse
- tan θ = Perpendicular / Base
- cot θ = Base / Perpendicular
Steps to solve:
- Identify the given side(s) and angle(s).
- Choose the appropriate trigonometric ratio based on the known and unknown sides.
- Set up the equation and solve for the unknown.
- Use trigonometric tables or known values for calculations (e.g., sin 30° = 1/2, tan 45° = 1).
Solving When One Side and One Acute Angle Are Given
- Use trigonometric ratios to find unknown sides or angles.
- Identify the known side and angle, then select the ratio involving the unknown.
- Steps:
- Write the trigonometric ratio (e.g., sin, cos, tan).
- Substitute known values.
- Solve for the unknown side or angle.
- Use trigonometric values (e.g., sin 30° = 1/2, tan 45° = 1).
Example 1: In triangle ABC, right-angled at B, side BC = 20 cm and ∠A = 30°. Find the length of AB.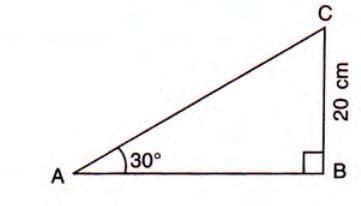
- Given: BC (base) = 20 cm, ∠A = 30°, right angle at B.
- Use cotangent: cot 30° = AB / BC.
- Since cot 30° = √3, we have AB / 20 = √3.
- Solve: AB = 20 × √3 = 20 × 1.732 = 34.64 cm.
- Answer: AB = 34.64 cm.
Example 2: In a right-angled triangle with hypotenuse 10 cm and perpendicular 5 cm, find angles x° and y°.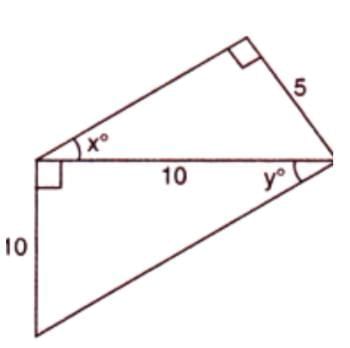
- Given: Perpendicular = 5 cm, Hypotenuse = 10 cm, Base = 10 cm.
- For angle x: sin x° = Perpendicular / Hypotenuse = 5 / 10 = 1/2.
- Since sin 30° = 1/2, x = 30°.
- For angle y: tan y° = Perpendicular / Base = 10 / 10 = 1.
- Since tan 45° = 1, y = 45°.
- Answer: x = 30°, y = 45°.
Solving When Two Sides Are Given
Use trigonometric ratios to find unknown angles.
Steps:
- Identify the two given sides (e.g., perpendicular, base, or hypotenuse).
- Choose the trigonometric ratio that relates the given sides to the unknown angle.
- Solve for the angle using known trigonometric values.
Example 3: In triangle ADC, AD = 10 cm, AC = 20 cm, find angle θ and length DC.
- Given: AD = 10 cm, AC = 20 cm, right angle at D.
- For angle θ: sin θ = AD / AC = 10 / 20 = 1/2.
- Since sin 30° = 1/2, θ = 30°.
- For DC: tan 30° = AD / DC = 10 / DC.
- Since tan 30° = 1 / √3, 1 / √3 = 10 / DC.
- Solve: DC = 10 × √3 = 10 × 1.732 = 17.32 cm.
- Answer: θ = 30°, DC = 17.32 cm.
Applications in Geometric Figures
- Right-angled triangles appear in figures like rhombuses, trapeziums, and real-world problems.
- Use properties of the figure to set up right triangles.
- Apply trigonometric ratios to find unknown sides or angles.
Example 4 (Rhombus)
In rhombus ABCD, each side is 10 cm, ∠A = 60°. Find lengths of diagonals AC and BD.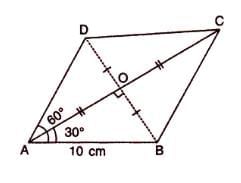
- Diagonals bisect each other at right angles, and ∠AOB = 90°, ∠OAB = 60° / 2 = 30°.
- In triangle AOB, AB = 10 cm.
- Find OB: sin 30° = OB / AB = OB / 10.
- Since sin 30° = 1/2, OB = 10 × 1/2 = 5 cm.
- Find OA: cos 30° = OA / AB = OA / 10.
- Since cos 30° = √3 / 2, OA = 10 × √3 / 2 = 5√3 = 5 × 1.732 = 8.66 cm.
- Diagonal AC = 2 × OA = 2 × 8.66 = 17.32 cm.
- Diagonal BD = 2 × OB = 2 × 5 = 10 cm.
- Answer: AC = 17.32 cm, BD = 10 cm.
Example 5 (Trapezium)
In trapezium ABCD, ∠C = 120°, DC = 28 cm, BC = 40 cm. Find AB, AD, and area.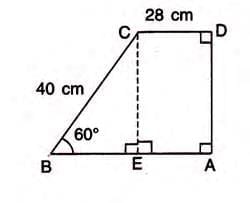
- Since CD || BA, ∠B = 180° - 120° = 60°.
- Draw CE ⊥ BA, forming right triangle CBE.
- Find CE: sin 60° = CE / 40.
- Since sin 60° = √3 / 2, CE = 40 × √3 / 2 = 20√3 cm.
- Find BE: cos 60° = BE / 40.
- Since cos 60° = 1/2, BE = 40 × 1/2 = 20 cm.
- AB = BE + EA = 20 + 28 = 48 cm (since EA = DC = 28 cm).
- AD = CE = 20√3 cm.
- Area = 1/2 × (AB + CD) × AD = 1/2 × (48 + 28) × 20√3 = 760√3 cm².
- Answer: AB = 48 cm, AD = 20√3 cm, Area = 760√3 cm².
Real-World Applications
- Right-angled triangles are used to calculate heights and distances in real-world scenarios.
- Examples include finding the height of a rocket or the length of a ladder.
- Steps:
- Draw a diagram to represent the problem as a right triangle.
- Identify given sides and angles.
- Use trigonometric ratios to find unknowns.
Example 6: A rocket rises 40 km vertically (PA), then 40 km at 60° to the vertical (AB). Find the height of the rocket at B and horizontal distance PC.
- Draw AD ⊥ BC, where ∠BAD = 90° - 60° = 30°.
- In triangle ABD, AB = 40 km.
- Find BD: sin 30° = BD / AB = BD / 40.
- Since sin 30° = 1/2, BD = 40 × 1/2 = 20 km.
- Height at B: BC = BD + DC = 20 + 40 = 60 km.
- Find AD: cos 30° = AD / AB = AD / 40.
- Since cos 60° = √3 / 2, AD = 40 × √3 / 2 = 20√3 km.
- Horizontal distance PC = AD = 20√3 = 20 × 1.732 = 34.64 km.
- Answer: Height = 60 km, PC = 34.64 km.
Solved Examples
Example 7: In triangle ABC, AB ⊥ BC, DC ⊥ BC, BD ⊥ AC, ∠D = 30°, DC = 60√3 m. Find AB.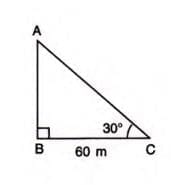
- In triangle BCD, ∠BCD = 90°, ∠D = 30°.
- Find BC: tan 30° = BC / DC = BC / 60√3.
- Since tan 30° = 1 / √3, BC / 60√3 = 1 / √3.
- Solve: BC = 60√3 / √3 = 60 m.
- In triangle BCD, ∠DBC = 180° - 90° - 30° = 60°.
- In triangle ABC, tan 30° = AB / BC = AB / 60.
- Since tan 30° = 1 / √3, AB / 60 = 1 / √3.
- Solve: AB = 60 / √3 = 20√3 m.
- Answer: AB = 20√3 m.
Example 8: In triangle ADC, AD = 10 cm, ∠ADC = 45°. Find AC.
- Given: AD = 10 cm, ∠ADC = 45°, right angle at D.
- Use tan 45°: tan 45° = AD / DC = 10 / DC.
- Since tan 45° = 1, 10 / DC = 1.
- Solve: DC = 10 cm.
- Use Pythagoras: AC² = AD² + DC² = 10² + 10² = 100 + 100 = 200.
- AC = √200 = 10√2 ≈ 14.14 cm.
- Answer: AC ≈ 14.14 cm.
The document Solution of Right Triangles Chapter Notes | Mathematics Class 9 ICSE is a part of the Class 9 Course Mathematics Class 9 ICSE.
All you need of Class 9 at this link: Class 9
|
28 videos|171 docs|28 tests
|
FAQs on Solution of Right Triangles Chapter Notes - Mathematics Class 9 ICSE
| 1. What is the significance of solving right triangles in geometry? |  |
Ans. Solving right triangles is essential in geometry because it allows us to find unknown side lengths and angles using the relationships defined by the Pythagorean theorem and trigonometric functions. This knowledge is useful in various fields, including architecture, engineering, and physics, where precise measurements are crucial.
| 2. How can one solve a right triangle when one side and one acute angle are given? | |
Ans. When one side and one acute angle of a right triangle are known, you can use trigonometric ratios. For example, if you have the length of the adjacent side and the angle, you can find the length of the opposite side using the tangent function. Similarly, you can find the hypotenuse using sine or cosine functions, depending on the given information.
| 3. What methods are used to solve a right triangle when two sides are known? | |
Ans. When two sides of a right triangle are known, you can use the Pythagorean theorem to find the third side. Additionally, you can use trigonometric functions like sine, cosine, and tangent to find the angles of the triangle. This approach helps in fully determining the triangle's dimensions.
| 4. What are some real-world applications of solving right triangles? | |
Ans. Real-world applications of solving right triangles include navigation, construction, and physics. For instance, engineers use right triangle principles to calculate loads and forces in structures, while pilots may use them to determine flight paths and distances over the Earth’s surface.
| 5. Can you provide an example of a geometric figure where solving right triangles is applied? | |
Ans. A common geometric figure where right triangles are applied is in the design of ramps. By using right triangle properties, designers can calculate the appropriate angle and length of the ramp to ensure it meets accessibility standards while also determining the required height and base measurements.
About this Document
Sep 07, 2025
Last updated
Related Exams
Document Description: Chapter Notes: Solution of Right Triangles for Class 9 2025 is part of Mathematics Class 9 ICSE preparation.
The notes and questions for Chapter Notes: Solution of Right Triangles have been prepared according to the Class 9 exam syllabus. Information about Chapter Notes: Solution of Right Triangles covers topics
like Introduction, Solving When One Side and One Acute Angle Are Given, Solving When Two Sides Are Given, Applications in Geometric Figures, Real-World Applications, Solved Examples and Chapter Notes: Solution of Right Triangles Example, for Class 9 2025 Exam. Find important definitions, questions, notes, meanings, examples, exercises and tests below for Chapter Notes: Solution of Right Triangles.
Introduction of Chapter Notes: Solution of Right Triangles in English is available as part of our Mathematics Class 9 ICSE
for Class 9 & Chapter Notes: Solution of Right Triangles in Hindi for Mathematics Class 9 ICSE course.
Download more important topics related with notes, lectures and mock test series for Class 9
Exam by signing up for free. Class 9: Solution of Right Triangles Chapter Notes | Mathematics Class 9 ICSE
Description
Full syllabus notes, lecture & questions for Solution of Right Triangles Chapter Notes | Mathematics Class 9 ICSE - Class 9 | Plus excerises question with solution to help you revise complete syllabus for Mathematics Class 9 ICSE | Best notes, free PDF download
Information about Chapter Notes: Solution of Right Triangles
In this doc you can find the meaning of Chapter Notes: Solution of Right Triangles defined & explained in the simplest way possible. Besides explaining types of
Chapter Notes: Solution of Right Triangles theory, EduRev gives you an ample number of questions to practice Chapter Notes: Solution of Right Triangles tests, examples and also practice Class 9
tests
Related Searches
Solution of Right Triangles Chapter Notes | Mathematics Class 9 ICSE
,shortcuts and tricks
,study material
,Important questions
,Solution of Right Triangles Chapter Notes | Mathematics Class 9 ICSE
,MCQs
,mock tests for examination
,video lectures
,Previous Year Questions with Solutions
,Solution of Right Triangles Chapter Notes | Mathematics Class 9 ICSE
,ppt
,practice quizzes
,Sample Paper
,Extra Questions
,Exam
,Viva Questions
,past year papers
,Semester Notes
,Summary
,Objective type Questions
,Free
;
Additional Information about Chapter Notes: Solution of Right Triangles for Class 9 Preparation
Chapter Notes: Solution of Right Triangles Free PDF Download
The Chapter Notes: Solution of Right Triangles is an invaluable resource that delves deep into the core of the Class 9 exam.
These study notes are curated by experts and cover all the essential topics and concepts, making your preparation more efficient and effective.
With the help of these notes, you can grasp complex subjects quickly, revise important points easily,
and reinforce your understanding of key concepts. The study notes are presented in a concise and easy-to-understand manner,
allowing you to optimize your learning process. Whether you're looking for best-recommended books, sample papers, study material,
or toppers' notes, this PDF has got you covered. Download the Chapter Notes: Solution of Right Triangles now and kickstart your journey towards success in the Class 9 exam.
Importance of Chapter Notes: Solution of Right Triangles
The importance of Chapter Notes: Solution of Right Triangles cannot be overstated, especially for Class 9 aspirants.
This document holds the key to success in the Class 9 exam.
It offers a detailed understanding of the concept, providing invaluable insights into the topic.
By knowing the concepts well in advance, students can plan their preparation effectively.
Utilize this indispensable guide for a well-rounded preparation and achieve your desired results.
Chapter Notes: Solution of Right Triangles
Chapter Notes: Solution of Right Triangles Notes offer in-depth insights into the specific topic to help you master it with ease.
This comprehensive document covers all aspects related to Chapter Notes: Solution of Right Triangles.
It includes detailed information about the exam syllabus, recommended books, and study materials for a well-rounded preparation.
Practice papers and question papers enable you to assess your progress effectively.
Additionally, the paper analysis provides valuable tips for tackling the exam strategically.
Access to Toppers' notes gives you an edge in understanding complex concepts.
Whether you're a beginner or aiming for advanced proficiency, Chapter Notes: Solution of Right Triangles Notes on EduRev are your ultimate resource for success.
Chapter Notes: Solution of Right Triangles Class 9 Questions
The "Chapter Notes: Solution of Right Triangles Class 9 Questions" guide is a valuable resource for all aspiring students preparing for the
Class 9 exam. It focuses on providing a wide range of practice questions to help students gauge
their understanding of the exam topics. These questions cover the entire syllabus, ensuring comprehensive preparation.
The guide includes previous years' question papers for students to familiarize themselves with the exam's format and difficulty level.
Additionally, it offers subject-specific question banks, allowing students to focus on weak areas and improve their performance.
Study Chapter Notes: Solution of Right Triangles on the App
Students of Class 9 can study Chapter Notes: Solution of Right Triangles alongwith tests & analysis from the EduRev app,
which will help them while preparing for their exam. Apart from the Chapter Notes: Solution of Right Triangles,
students can also utilize the EduRev App for other study materials such as previous year question papers, syllabus, important questions, etc.
The EduRev App will make your learning easier as you can access it from anywhere you want.
The content of Chapter Notes: Solution of Right Triangles is prepared as per the latest Class 9 syllabus.
|
© EduRev
|
Education Revolution
|
|
Signup to see your scores
go up within 7 days!
Access 1000+ FREE Docs, Videos and Tests
Takes less than 10 seconds to signup