Class 9 Exam > Class 9 Notes > Mathematics Class 9 ICSE > Chapter Notes: Complementary Angles
Complementary Angles Chapter Notes | Mathematics Class 9 ICSE PDF Download
Introduction
Imagine you're slicing a pizza, and you cut two pieces that perfectly fit together to form a right angle. That’s the essence of complementary angles! In this exciting chapter, we dive into the world of angles that team up to make 90°, exploring their trigonometric ratios and how they simplify complex problems. From sine to tangent, we’ll uncover how these angles relate to each other in a right-angled triangle, making math both fun and intuitive. Get ready to discover the magic of complementary angles and their applications!
- Trigonometric ratios for standard angles (0°, 30°, 45°, 60°, 90°) have been studied earlier.
- Focus of this chapter: Understanding trigonometric ratios of complementary angles.
- Learn how to apply these ratios in various mathematical problems.
Concept of Trigonometric Ratios of Complementary Angles
Definition: Two acute angles are complementary if their sum equals 90°.
Steps to Identify Complementary Angles:
- Add the two angles.
- Check if the sum is 90°.
Finding the Complement:
- Subtract the given angle from 90° to find its complement.
Example 1: For 30° and 60°, 30° + 60° = 90°, so they are complementary. For 48°, its complement is 90° - 48° = 42°.
Complementary Angles for Sine (sin) and Cosine (cos)
In a right-angled triangle ABC (right angle at B), if ∠ACB = θ, then ∠CAB = 90° - θ.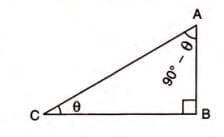
Steps to Derive Relationships:
- sin θ = perpendicular/hypotenuse = AB/AC.
- cos (90° - θ) = base/hypotenuse = AB/AC.
- Thus, sin θ = cos (90° - θ).
- cos θ = base/hypotenuse = BC/AC.
- sin (90° - θ) = perpendicular/hypotenuse = BC/AC.
- Thus, sin (90° - θ) = cos θ.
Formulas:
- cos (90° - θ) = sin θ
- sin (90° - θ) = cos θ
Example 1: In triangle ABC (∠B = 90°), if ∠ACB = 30°, then ∠CAB = 60°. Here, sin 30° = cos 60° = 1/2.
Example 2: Evaluate (cos 47° / sin 43°)2 + (sin 72° / cos 18°)2 - 2 cos245°.
- cos 47° = cos (90° - 43°) = sin 43°.
- sin 72° = sin (90° - 18°) = cos 18°.
- Expression becomes: (sin 43° / sin 43°)2 + (cos 18° / cos 18°)2 - 2 (1/√2)2.
- = 12 + 12 - 2 × 1/2 = 1 + 1 - 1 = 1.
- Answer: 1
Complementary Angles for Tangent (tan) and Cotangent (cot)
In triangle ABC (∠B = 90°), if ∠ACB = θ, then ∠CAB = 90° - θ.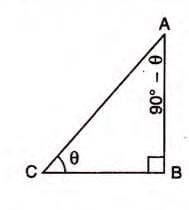
Steps to Derive Relationships:
- tan θ = perpendicular/base = AB/BC.
- cot (90° - θ) = base/perpendicular = AB/BC.
- Thus, tan θ = cot (90° - θ).
- cot θ = base/perpendicular = BC/AB.
- tan (90° - θ) = perpendicular/base = BC/AB.
- Thus, cot θ = tan (90° - θ).
Formulas:
- cot (90° - θ) = tan θ
- tan (90° - θ) = cot θ
Example 1: In triangle ABC, if ∠ACB = 45°, then ∠CAB = 45°. Here, tan 45° = cot 45° = 1.
Example 2: Prove that (tan 72° / cot 18°) - (cot 72° / tan 18°) = 0.
- tan 72° = tan (90° - 18°) = cot 18°.
- cot 72° = cot (90° - 18°) = tan 18°.
- Expression becomes: (cot 18° / cot 18°) - (tan 18° / tan 18°).
- = 1 - 1 = 0.
- Hence Proved.
Complementary Angles for Secant (sec) and Cosecant (cosec)
Formulas:
- sec (90° - θ) = cosec θ
- cosec (90° - θ) = sec θ
Example 1: sec (90° - 35°) = cosec 35°.
Example 2: Evaluate cosec 82° - sec 8°.
- cosec 82° = cosec (90° - 8°) = sec 8°.
- Expression becomes: sec 8° - sec 8° = 0.
- Answer: 0
General Relationships for Complementary Angles A and B
If A + B = 90°, then A and B are complementary.
Formulas:
- sin A = cos B
- cos A = sin B
- tan A = cot B
- cot A = tan B
- sec A = cosec B
- cosec A = sec B
Example 1: If A = 30° and B = 60°, then sin 30° = cos 60° = 1/2.
Additional Proofs and Evaluations
Proof in Triangle ABC:
- For triangle ABC, A + B + C = 180°.
- Thus, A + B = 180° - C.
- (A + B)/2 = 90° - C/2.
- sec ((A + B)/2) = sec (90° - C/2) = cosec (C/2).
Example 1: In triangle ABC, prove sec ((A + B)/2) = cosec (C/2).
Example 2: Evaluate (2 tan 53° / cot 37°) - (cot 80° / tan 10°).
- tan 53° = tan (90° - 37°) = cot 37°.
- cot 80° = cot (90° - 10°) = tan 10°.
- Expression becomes: (2 cot 37° / cot 37°) - (tan 10° / tan 10°).
- = 2 - 1 = 1.
- Answer: 1
- cot 37° = cot (90° - 53°) = tan 53°.
- tan 10° = tan (90° - 80°) = cot 80°.
- Expression: (2 tan 53° / tan 53°) - (cot 80° / cot 80°).
- = 2 - 1 = 1.
Example 2: Given cos 38° sec (90° - 2A) = 1, find A.
- sec (90° - 2A) = cosec 2A.
- Expression: cos 38° × cosec 2A = 1.
- cosec 2A = 1 / cos 38°.
- sin 2A = cos 38° = cos (90° - 52°) = sin 52°.
- sin 2A = sin 52° implies 2A = 52°.
- A = 26°.
- Answer: A = 26°
The document Complementary Angles Chapter Notes | Mathematics Class 9 ICSE is a part of the Class 9 Course Mathematics Class 9 ICSE.
All you need of Class 9 at this link: Class 9
|
28 videos|171 docs|28 tests
|
FAQs on Complementary Angles Chapter Notes - Mathematics Class 9 ICSE
| 1. What are complementary angles in trigonometry? |  |
Ans.Complementary angles are two angles whose measures add up to 90 degrees. In trigonometry, the concept of complementary angles is crucial as it helps establish relationships between the trigonometric ratios of these angles.
| 2. How do the sine and cosine functions relate to complementary angles? | |
Ans.The sine of an angle is equal to the cosine of its complementary angle. This can be expressed as sin(A) = cos(90° - A), where A is the angle in question. This relationship is a fundamental part of trigonometric identities.
| 3. What is the relationship between tangent and cotangent for complementary angles? | |
Ans.The tangent of an angle is equal to the cotangent of its complementary angle. This means that tan(A) = cot(90° - A). This relationship is useful in simplifying trigonometric expressions and solving equations.
| 4. Can you explain the relationships for secant and cosecant in terms of complementary angles? | |
Ans.The secant of an angle is equal to the cosecant of its complementary angle. This can be stated as sec(A) = cosec(90° - A). This identity helps in understanding how these functions interact with each other in trigonometric calculations.
| 5. What are some general relationships for complementary angles A and B in trigonometry? | |
Ans.Some general relationships for complementary angles A and B include:
- sin(A) = cos(B)
- cos(A) = sin(B)
- tan(A) = cot(B)
- cot(A) = tan(B)
- sec(A) = cosec(B)
- cosec(A) = sec(B).
These relationships are essential in solving various trigonometric problems and proofs.
About this Document
Sep 07, 2025
Last updated
Related Exams
Document Description: Chapter Notes: Complementary Angles for Class 9 2025 is part of Mathematics Class 9 ICSE preparation.
The notes and questions for Chapter Notes: Complementary Angles have been prepared according to the Class 9 exam syllabus. Information about Chapter Notes: Complementary Angles covers topics
like Introduction, Concept of Trigonometric Ratios of Complementary Angles, Complementary Angles for Sine (sin) and Cosine (cos), Complementary Angles for Tangent (tan) and Cotangent (cot), Complementary Angles for Secant (sec) and Cosecant (cosec), General Relationships for Complementary Angles A and B, Additional Proofs and Evaluations and Chapter Notes: Complementary Angles Example, for Class 9 2025 Exam. Find important definitions, questions, notes, meanings, examples, exercises and tests below for Chapter Notes: Complementary Angles.
Introduction of Chapter Notes: Complementary Angles in English is available as part of our Mathematics Class 9 ICSE
for Class 9 & Chapter Notes: Complementary Angles in Hindi for Mathematics Class 9 ICSE course.
Download more important topics related with notes, lectures and mock test series for Class 9
Exam by signing up for free. Class 9: Complementary Angles Chapter Notes | Mathematics Class 9 ICSE
Description
Full syllabus notes, lecture & questions for Complementary Angles Chapter Notes | Mathematics Class 9 ICSE - Class 9 | Plus excerises question with solution to help you revise complete syllabus for Mathematics Class 9 ICSE | Best notes, free PDF download
Information about Chapter Notes: Complementary Angles
In this doc you can find the meaning of Chapter Notes: Complementary Angles defined & explained in the simplest way possible. Besides explaining types of
Chapter Notes: Complementary Angles theory, EduRev gives you an ample number of questions to practice Chapter Notes: Complementary Angles tests, examples and also practice Class 9
tests
Related Searches
practice quizzes
,Objective type Questions
,Extra Questions
,Complementary Angles Chapter Notes | Mathematics Class 9 ICSE
,shortcuts and tricks
,ppt
,Exam
,Important questions
,Previous Year Questions with Solutions
,Complementary Angles Chapter Notes | Mathematics Class 9 ICSE
,mock tests for examination
,Summary
,Semester Notes
,MCQs
,Viva Questions
,Free
,Complementary Angles Chapter Notes | Mathematics Class 9 ICSE
,Sample Paper
,video lectures
,past year papers
,study material
;
Additional Information about Chapter Notes: Complementary Angles for Class 9 Preparation
Chapter Notes: Complementary Angles Free PDF Download
The Chapter Notes: Complementary Angles is an invaluable resource that delves deep into the core of the Class 9 exam.
These study notes are curated by experts and cover all the essential topics and concepts, making your preparation more efficient and effective.
With the help of these notes, you can grasp complex subjects quickly, revise important points easily,
and reinforce your understanding of key concepts. The study notes are presented in a concise and easy-to-understand manner,
allowing you to optimize your learning process. Whether you're looking for best-recommended books, sample papers, study material,
or toppers' notes, this PDF has got you covered. Download the Chapter Notes: Complementary Angles now and kickstart your journey towards success in the Class 9 exam.
Importance of Chapter Notes: Complementary Angles
The importance of Chapter Notes: Complementary Angles cannot be overstated, especially for Class 9 aspirants.
This document holds the key to success in the Class 9 exam.
It offers a detailed understanding of the concept, providing invaluable insights into the topic.
By knowing the concepts well in advance, students can plan their preparation effectively.
Utilize this indispensable guide for a well-rounded preparation and achieve your desired results.
Chapter Notes: Complementary Angles
Chapter Notes: Complementary Angles Notes offer in-depth insights into the specific topic to help you master it with ease.
This comprehensive document covers all aspects related to Chapter Notes: Complementary Angles.
It includes detailed information about the exam syllabus, recommended books, and study materials for a well-rounded preparation.
Practice papers and question papers enable you to assess your progress effectively.
Additionally, the paper analysis provides valuable tips for tackling the exam strategically.
Access to Toppers' notes gives you an edge in understanding complex concepts.
Whether you're a beginner or aiming for advanced proficiency, Chapter Notes: Complementary Angles Notes on EduRev are your ultimate resource for success.
Chapter Notes: Complementary Angles Class 9 Questions
The "Chapter Notes: Complementary Angles Class 9 Questions" guide is a valuable resource for all aspiring students preparing for the
Class 9 exam. It focuses on providing a wide range of practice questions to help students gauge
their understanding of the exam topics. These questions cover the entire syllabus, ensuring comprehensive preparation.
The guide includes previous years' question papers for students to familiarize themselves with the exam's format and difficulty level.
Additionally, it offers subject-specific question banks, allowing students to focus on weak areas and improve their performance.
Study Chapter Notes: Complementary Angles on the App
Students of Class 9 can study Chapter Notes: Complementary Angles alongwith tests & analysis from the EduRev app,
which will help them while preparing for their exam. Apart from the Chapter Notes: Complementary Angles,
students can also utilize the EduRev App for other study materials such as previous year question papers, syllabus, important questions, etc.
The EduRev App will make your learning easier as you can access it from anywhere you want.
The content of Chapter Notes: Complementary Angles is prepared as per the latest Class 9 syllabus.
|
© EduRev
|
Education Revolution
|
|
Signup on EduRev and stay on top of your study goals
10M+ students crushing their study goals daily