Matrices Chapter Notes | Mathematics Class 10 ICSE PDF Download
Introduction
Welcome to the fascinating world of matrices, where numbers come together in a structured dance of rows and columns! Matrices are like organized grids that help us solve problems in mathematics, science, and even computer graphics. Imagine them as a powerful tool to manage data, perform calculations, and systematically unlock patterns. In this chapter, we'll explore what matrices are, their types, and how to perform operations like addition, subtraction, and multiplication. Get ready to dive into this structured yet exciting mathematical adventure!
Matrix

- A matrix is a rectangular grid of numbers arranged in rows and columns.
- Each number in the matrix is called an element.
- Rows are horizontal lines, and columns are vertical lines.
- The plural of matrix is matrices.
Example: The following are examples of matrices:
- [5 1] (a Row matrix)
- [5 3; 1 2] (a 2x2 matrix)
Order of a Matrix

- The order of a matrix is defined as the number of rows multiplied by the number of columns (rows × columns).
- If a matrix has m rows and n columns, its order is written as m × n, read as "m by n".
- The number of rows is always stated first, followed by the number of columns.
- Example: For the matrix
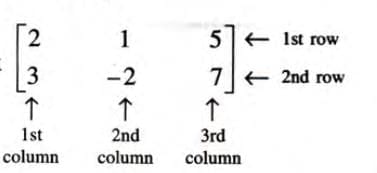
- It has 2 rows and 3 columns, so its order is 2 × 3 (read as 2 by 3).
Elements of a Matrix
- Each number or value in a matrix is called an element.
- The total number of elements in a matrix is calculated as the product of the number of rows and columns.
- Formula: Total elements = Number of rows × Number of columns
- Example: For the matrix A = [2 4 -3; 0 1 2], it has 2 rows and 3 columns, so the number of elements = 2 × 3 = 6.
- A matrix with 6 elements can have orders like 1 × 6, 2 × 3, 3 × 2, or 6 × 1.
Types of Matrices
Row Matrix:
- A matrix with only one row is called a row matrix or row vector.
- Example: A is a row matrix with order 1 × 3.
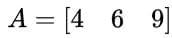
Column Matrix:
- A matrix with only one column is called a column matrix or column vector.
- Example: A is a column matrix with order 3 × 1.
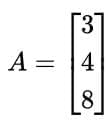
Square Matrix:
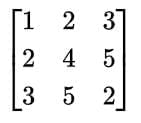
- A matrix with an equal number of rows and columns is called a square matrix.
- Example: Following is a square matrix with order 3 × 3.
Rectangular Matrix:
- A matrix where the number of rows is not equal to the number of columns is called a rectangular matrix.
- Example: Following is a rectangular matrix with order 2 × 4.

Zero or Null Matrix:
- A matrix where all elements are zero is called a zero or null matrix.
- Example: Following is a zero matrix.
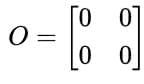
Diagonal Matrix:
- A square matrix where all elements are zero except those on the main diagonal (top-left to bottom-right) is called a diagonal matrix.
- Example: Following is a diagonal matrix.

Unit or Identity Matrix:
- A diagonal matrix where all elements on the main diagonal are 1 and all other elements are 0 is called a unit or identity matrix, denoted by I.
- Example: Following is a 3 × 3 identity matrix.
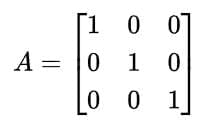
Transpose of a Matrix
- The transpose of a matrix is obtained by interchanging its rows and columns.
- If A is a matrix, its transpose is denoted by At.
- Example: If A is a matrix, then At is the transpose of A.
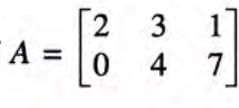
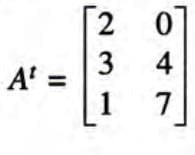
Equality of Matrices
- Two matrices are equal if:
- They have the same order.
- Their corresponding elements are equal.
- Example: If A =
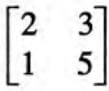 and B =
and B = 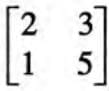 , then A = B because they have the same order (2 × 2) and identical elements.
, then A = B because they have the same order (2 × 2) and identical elements. - Solved Example: Find x, y, a, and b if
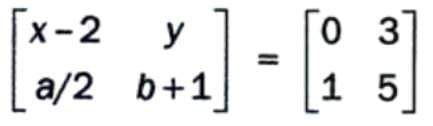
- Since the matrices are equal, equate corresponding elements:
- x - 2 = 0 → x = 2
- y = 3
- a/2 = 1 → a = 2
- b + 1 = 5 → b = 4
- Answer: x = 2, y = 3, a = 2, b = 4
Addition of Matrices
- Two matrices can be added only if they have the same order.
- Addition involves adding corresponding elements of both matrices.
- Formula: If A = [aij] and B = [bij], then A + B = [aij + bij]
- Example: If
 then A + B =
then A + B = 
- Properties of Matrix Addition:
- Commutative: A + B = B + A
- Associative: (A + B) + C = A + (B + C)
- Solved Example: Given A = [5 4] and B = [-3 0], find A + B and B + A.
- A + B = [5 4] + [-3 0] = [5-3 4+0] = [2 4]
- B + A = [-3 0] + [5 4] = [-3+5 0+4] = [2 4]
- Conclusion: A + B = B + A, so matrix addition is commutative.
Subtraction of Matrices
- Two matrices can be subtracted only if they have the same order.
- Subtraction involves subtracting corresponding elements of the second matrix from the first.
- Formula: If A = [aij] and B = [bij], then A - B = [aij - bij]
- Example: If
then A - B = 
Additive Identity
- The zero (null) matrix acts as the additive identity in matrices.
- Adding a zero matrix of the same order to any matrix leaves the matrix unchanged.
- Formula: A + O = O + A = A, where O is the zero matrix of the same order as A.
- Example:
Additive Inverse
- The additive inverse of a matrix A is -A, such that A + (-A) = (-A) + A = zero matrix.
- The negative of a matrix is obtained by multiplying each element by -1.
- Formula: A + (-A) = O, where O is the zero matrix.
- Example: If
 ,
, - and
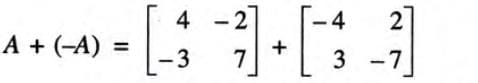
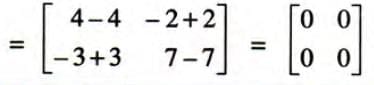
Solving Matrix Equations
- To solve A + X = B, where A, B, and X are matrices of the same order, subtract A from both sides: X = B - A.
- Example: If
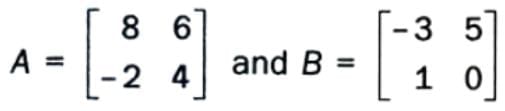 , solve for X such that A + X = B.
, solve for X such that A + X = B. - X = B - A
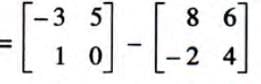
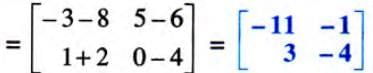 .
.
Multiplication of a Matrix by a Scalar
- Multiplying a matrix by a scalar involves multiplying each element of the matrix by that scalar.
- Formula: If k is a scalar and A = [aij], then kA = [k × aij].
- Example: 3[4 1] = [3×4 3×1] = [12 3].
Multiplication of Matrices
- Two matrices A and B can be multiplied if the number of columns in A equals the number of rows in B.
- Formula: If A is m × n and B is n × p, then AB is m × p.
Steps for multiplication:
- Multiply each element of a row of A by the corresponding element of a column of B and sum the products.
- Repeat for each row of A and each column of B.
Example:
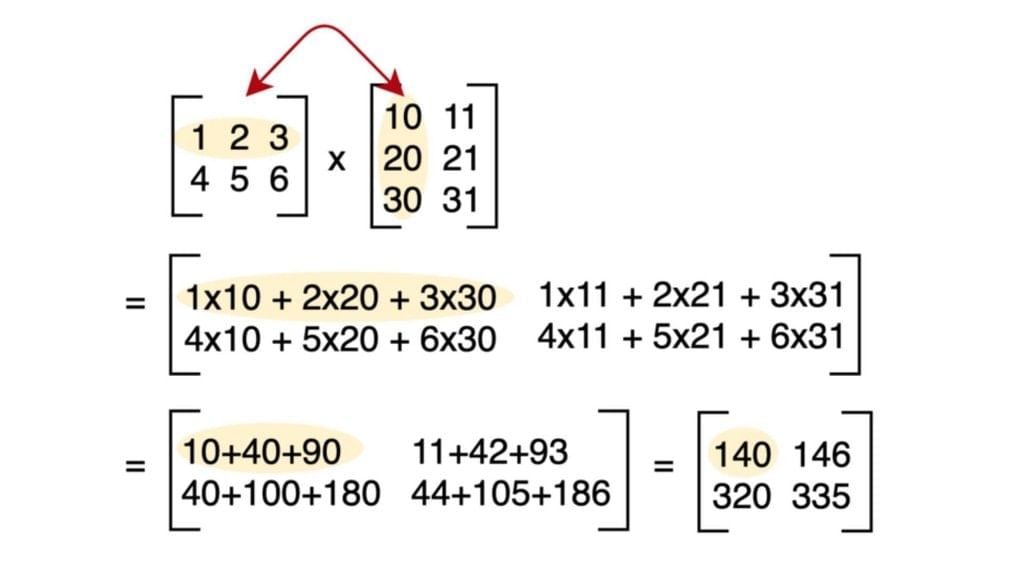
Properties of Matrix Multiplication:
- Not commutative: AB ≠ BA in general.
- Associative: (AB)C = A(BC).
- Distributive: A(B + C) = AB + AC, (A + B)C = AC + BC.
- Zero product: If AB = 0, it does not imply A = 0 or B = 0.
- Cancellation law does not apply: If AB = AC, B ≠ C unless A is invertible.
Example 2: Given A = [-3 3; 2 -2] and B = [4 6; 4 6], find AB.
- AB = [-3 3; 2 -2][4 6; 4 6] = [-12+12 -18+18; 8-8 12-12] = [0 0; 0 0]
- Conclusion: The product of two non-zero matrices can be a zero matrix.
Identity Matrix for Multiplication
The identity matrix I acts as the multiplicative identity, such that A × I = I × A = A for any matrix A of the same order.
- Example 1: If A =
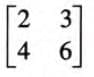 and I =
and I = 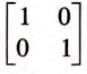 ,
,
then A × I =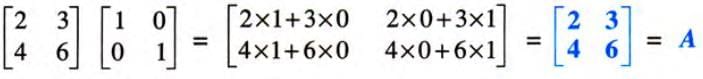
- Example 2: If A =
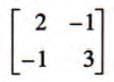 , evaluate A2- 3A + 2I, where I is the 2 × 2 identity matrix.
, evaluate A2- 3A + 2I, where I is the 2 × 2 identity matrix. - A2 = A × A =
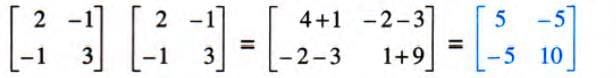
- A2 - 3A + 2I =

- =

- =

|
74 videos|213 docs|30 tests
|
FAQs on Matrices Chapter Notes - Mathematics Class 10 ICSE
| 1. What is a matrix and how is it represented? |  |
| 2. How do you determine the order of a matrix? |  |
| 3. What is the transpose of a matrix and how is it calculated? |  |
| 4. How do you check if two matrices are equal? |  |
| 5. What are the additive identity and its role in matrix addition? |  |





















