Class 10 Exam > Class 10 Notes > Mathematics Class 10 ICSE > Chapter Notes: Section and Mid-Point Formula
Section and Mid-Point Formula Chapter Notes | Mathematics Class 10 ICSE PDF Download
| Table of contents |

|
| Introduction |

|
| The Section Formula |

|
| Points of Trisection |

|
| Mid-Point Formula |

|
| Centroid of a Triangle |

|
Introduction
Imagine you’re a treasure hunter on a giant graph paper, where every dot marks a clue to a hidden prize! The "Section and Mid-Point Formula" chapter is your map, guiding you to measure distances, split paths, or find the exact middle of a line. It’s like having a superpower to navigate the world of coordinate geometry with ease. Whether you’re dividing a line into parts or finding a triangle’s center, this chapter makes it simple and fun. Let’s jump into this math adventure and uncover the secrets of points and lines!
Coordinate geometry helps you explore points on a graph (called a Cartesian plane).
It lets you solve problems about lines connecting two points by:
- Finding how far apart two points are.
- Locating a point that splits a line into a specific ratio.
- Finding the middle point of a line.
- Writing the equation of a line passing through two points.
- Figuring out the equation of a line that cuts another line in half at a right angle (perpendicular bisector).
The Section Formula
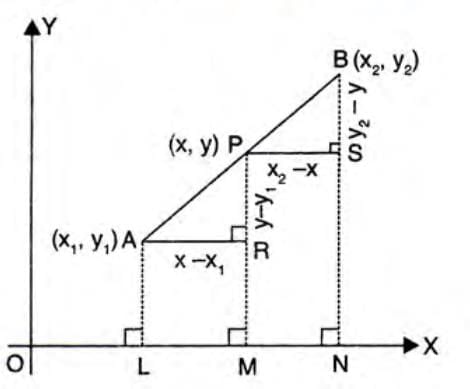
- This formula finds the coordinates of a point that splits a line segment into a given ratio, like cutting a rope into two pieces of specific lengths.
- If point P divides the line from A(x1, y1) to B(x2, y2) in the ratio m1:m2, it means the length AP:PB = m1:m2.
- Formula: Coordinates of P =
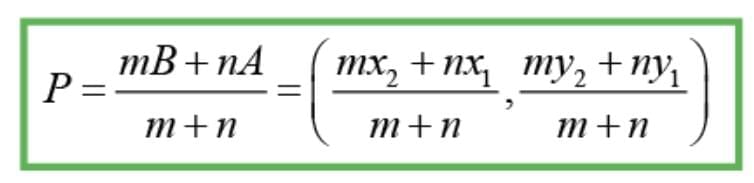
- Steps to find the point:
- Write the coordinates of points A and B.
- Check the ratio m1:m2 (how the line is divided).
- Put the values into the formula for x and y coordinates.
- Simplify to get the coordinates of point P.
- To find the ratio when you know the dividing point:
- Use the same formula, but set the point’s coordinates equal to x and y.
- Solve for m1 and m2 to find the ratio.
- Alternative Method (k:1 ratio): Assume the ratio is k:1. Then,
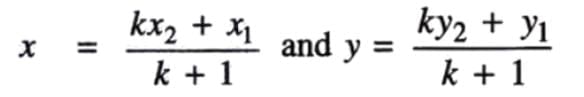 Solve for k to get the ratio k:1.
Solve for k to get the ratio k:1.
Example 1: Find the coordinates of point P dividing the line from A(4, -5) to B(6, 3) in the ratio 2:5.
- Step 1: A(4, -5), B(6, 3), ratio m1:m2 = 2:5.
- Step 2: x-coordinate = (2 × 6 + 5 × 4)/(2 + 5) = (12 + 20)/7 = 32/7.
- Step 3: y-coordinate = (2 × 3 + 5 × -5)/(2 + 5) = (6 - 25)/7 = -19/7.
- Step 4: P = (32/7, -19/7).
Example 2: Find the ratio in which point (5, 4) divides the line from (2, 1) to (7, 6).
- Step 1: Points (2, 1), (7, 6), P(5, 4).
- Step 2: Use x-coordinate: 5 = (m1 × 7 + m2 × 2)/(m1 + m2).
- Step 3: Multiply: 5(m1 + m2) = 7m1 + 2m2.
- Step 4: Simplify: 5m1 + 5m2 = 7m1 + 2m2 → 3m2 = 2m1 → m1:m2 = 3:2.
- Alternative: 5 = (k × 7 + 2)/(k + 1) → 5k + 5 = 7k + 2 → 3 = 2k → k = 3/2. Ratio = 3:2.
Solved Example: Find the ratio in which the line joining (4, 2) and (3, -5) is divided by the x-axis. Also, find the point of intersection.
- Step 1: Point on x-axis has y = 0. Let ratio be k:1, point = (x, 0).
- Step 2: Use y-coordinate: 0 = (k × -5 + 2)/(k + 1).
- Step 3: Solve: -5k + 2 = 0 → k = 2/5. Ratio = 2:5.
- Step 4: x-coordinate = (2 × 3 + 5 × 4)/(2 + 5) = (6 + 20)/7 = 26/7.
- Step 5: Point of intersection = (26/7, 0).
Points of Trisection
- Trisection means splitting a line into three equal parts, like cutting a stick into three equal pieces.
- Points P and Q divide line AB so that AP = PQ = QB.
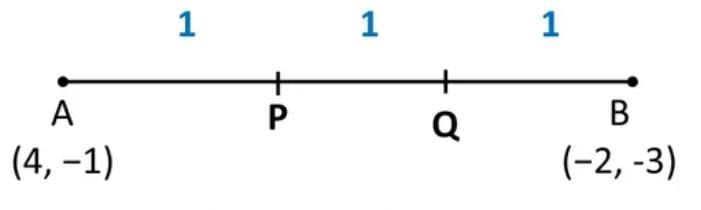
- P divides AB in ratio 1:2 (AP:PB).
- Q divides AB in ratio 2:1 (AQ:QB).
- Use the section formula with these ratios to find coordinates of P and Q.
- To check if a point trisects a line, verify if it divides in 1:2 or 2:1.
Example 1: Find the points of trisection of the line joining A(6, -2) and B(-8, 10).

- Step 1: For P (ratio 1:2): x = (1 × -8 + 2 × 6)/(1 + 2) = (-8 + 12)/3 = 4/3.
- Step 2: y = (1 × 10 + 2 × -2)/(1 + 2) = (10 - 4)/3 = 2. P = (4/3, 2).
- Step 3: For Q (ratio 2:1): x = (2 × -8 + 1 × 6)/(2 + 1) = (-16 + 6)/3 = -10/3.
- Step 4: y = (2 × 10 + 1 × -2)/(2 + 1) = (20 - 2)/3 = 6. Q = (-10/3, 6).
Example 2: Show that P(3, m-5) is a point of trisection of the line joining A(4, -2) and B(1, 4). Find m.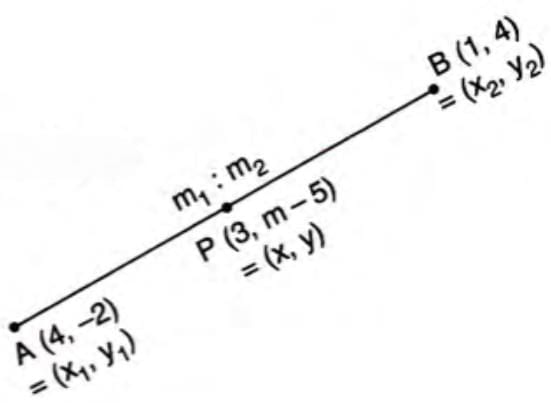

- Step 1: P divides AB in 1:2 or 2:1. Try 1:2.
- Step 2: x-coordinate: 3 = (1 × 1 + 2 × 4)/(1 + 2) = (1 + 8)/3 = 3 (correct).
- Step 3: y-coordinate: m - 5 = (1 × 4 + 2 × -2)/(1 + 2) = (4 - 4)/3 = 0.
- Step 4: Solve: m - 5 = 0 → m = 5.
- Step 5: P(3, 0) divides in 1:2, so it’s a trisection point.
Mid-Point Formula
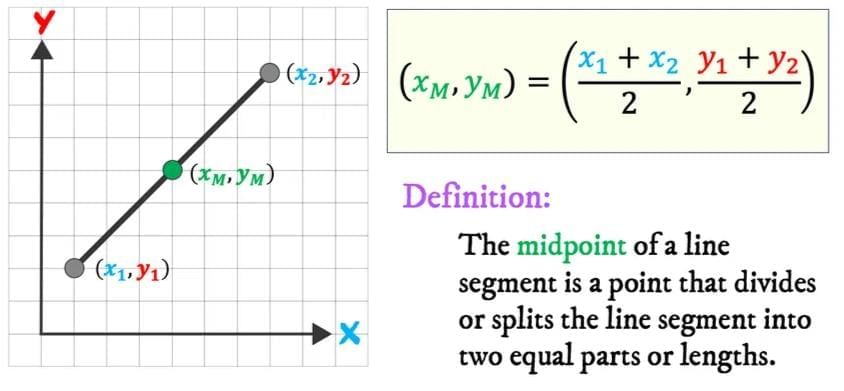
- This formula finds the middle point of a line segment, like finding the center of a bridge.
- For points A(x1, y1) and B(x2, y2), the midpoint P splits AB in ratio 1:1.
- Formula: Midpoint = ((x1 + x2)/2, (y1 + y2)/2)
- Steps:
- Add the x-coordinates of A and B, then divide by 2.
- Add the y-coordinates of A and B, then divide by 2.
- The result gives the midpoint’s coordinates.
Example 1: Find the midpoint of the line joining P(4, -6) and Q(-2, 4).
- Step 1: x-coordinate = (4 + (-2))/2 = 2/2 = 1.
- Step 2: y-coordinate = (-6 + 4)/2 = -2/2 = -1.
- Step 3: Midpoint = (1, -1).
Example 2: The midpoint of line segment AB is (-3, 5). A lies on the x-axis, B on the y-axis. Find A and B.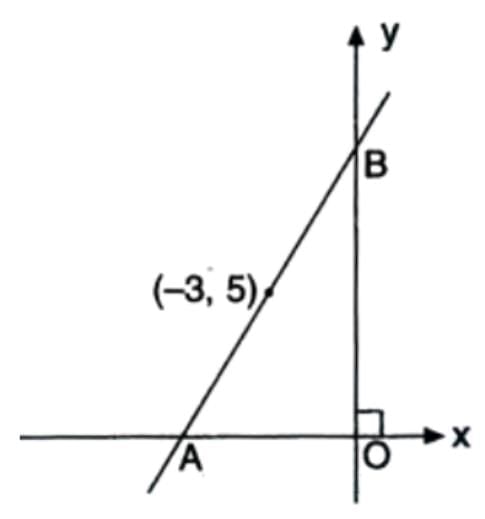

- Step 1: Let A = (x, 0), B = (0, y).
- Step 2: Midpoint = ((x + 0)/2, (0 + y)/2) = (-3, 5).
- Step 3: x/2 = -3 → x = -6; y/2 = 5 → y = 10.
- Step 4: A = (-6, 0), B = (0, 10).
Centroid of a Triangle
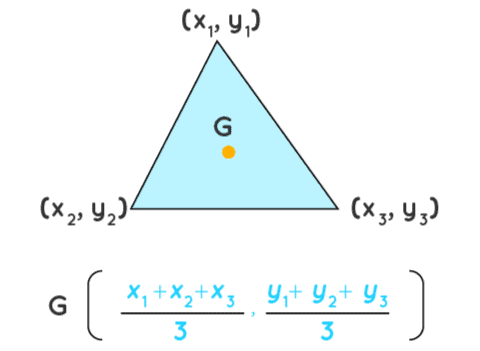
- The centroid is the point where all three medians (lines from a vertex to the midpoint of the opposite side) of a triangle meet.
- It divides each median in the ratio 2:1 (closer to the vertex).
- Formula: Centroid = ((x1 + x2 + x3)/3, (y1 + y2 + y3)/3) for vertices A(x1, y1), B(x2, y2), C(x3, y3).
- Steps:
- List the coordinates of vertices A, B, and C.
- Add all x-coordinates and divide by 3.
- Add all y-coordinates and divide by 3.
- The result is the centroid’s coordinates.
- Alternative method:
- Find the midpoint of one side (e.g., BC).
- Use the section formula to find the point dividing the median (from A to midpoint of BC) in ratio 2:1.
Example 1: Find the centroid of triangle ABC with vertices A(-2, 3), B(6, 7), C(4, 1).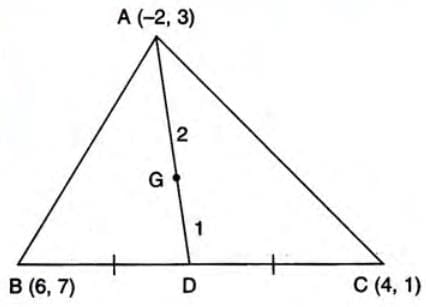

- Step 1: x = (-2 + 6 + 4)/3 = 8/3.
- Step 2: y = (3 + 7 + 1)/3 = 11/3.
- Step 3: Centroid = (8/3, 11/3).
- Alternative: Midpoint D of BC = ((6 + 4)/2, (7 + 1)/2) = (5, 4).
- Step 4: Centroid G divides AD in 2:1: x = (2 × 5 + 1 × -2)/(2 + 1) = 8/3.
- Step 5: y = (2 × 4 + 1 × 3)/(2 + 1) = 11/3.
- Centroid = (8/3, 11/3).
Example 2: In triangle OBC, O(0, 0), B(-6, 9), C(12, -3). P divides OB in 1:2, Q divides OC in 1:2. Show PQ = 1/3 BC.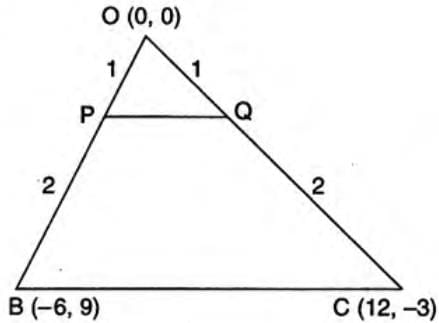

- Step 1: For P: x = (1 × -6 + 2 × 0)/(1 + 2) = -6/3 = -2; y = (1 × 9 + 2 × 0)/(1 + 2) = 9/3 = 3. P = (-2, 3).
- Step 2: For Q: x = (1 × 12 + 2 × 0)/(1 + 2) = 12/3 = 4; y = (1 × -3 + 2 × 0)/(1 + 2) = -3/3 = -1. Q = (4, -1).
- Step 3: PQ = √((4 - (-2))2 + (-1 - 3)2) = √(62 + (-4)2) = √(36 + 16) = 2√13.
- Step 4: BC = √((12 - (-6))2 + (-3 - 9)2) = √(182 + (-12)2) = √(324 + 144) = 6√13.
- Step 5: PQ = 2√13, BC = 6√13 → PQ = 1/3 BC.
The document Section and Mid-Point Formula Chapter Notes | Mathematics Class 10 ICSE is a part of the Class 10 Course Mathematics Class 10 ICSE.
All you need of Class 10 at this link: Class 10
|
74 videos|213 docs|30 tests
|
FAQs on Section and Mid-Point Formula Chapter Notes - Mathematics Class 10 ICSE
| 1. What is the Section Formula and how is it derived ? |  |
Ans. The Section Formula is used to find the coordinates of a point that divides a line segment into a specific ratio. If point P divides the line segment joining points A(x1, y1) and B(x2, y2) in the ratio m:n, the coordinates of point P can be determined using the formula: P(x, y) = ((mx2 + nx1) / (m + n), (my2 + ny1) / (m + n)). This formula is derived from the concept of weighted averages based on the ratio in which the segment is divided.
| 2. How do you find the points of trisection of a line segment ? |  |
Ans. To find the points of trisection of a line segment, you divide the segment into three equal parts. If you have two endpoints A(x1, y1) and B(x2, y2), the coordinates of the points of trisection, say T1 and T2, can be found using the Section Formula. For T1, which divides the segment in the ratio 1:2, use T1 = ((2x1 + x2) / 3, (2y1 + y2) / 3). For T2, which divides it in the ratio 2:1, use T2 = ((x1 + 2x2) / 3, (y1 + 2y2) / 3).
| 3. What is the Mid-Point Formula and how is it used ? |  |
Ans. The Mid-Point Formula is used to find the midpoint of a line segment whose endpoints are given. If the endpoints are A(x1, y1) and B(x2, y2), the midpoint M can be calculated as M = ((x1 + x2) / 2, (y1 + y2) / 2). This formula is useful in various applications, such as geometry, computer graphics, and coordinate geometry, to determine the center point of a segment.
| 4. How do you calculate the centroid of a triangle using coordinates ? |  |
Ans. The centroid of a triangle, which is the point where the three medians intersect, can be calculated using the coordinates of its vertices. If the vertices of the triangle are A(x1, y1), B(x2, y2), and C(x3, y3), the centroid G can be found using the formula G = ((x1 + x2 + x3) / 3, (y1 + y2 + y3) / 3). This point represents the average of the x-coordinates and the average of the y-coordinates of the triangle's vertices.
| 5. Why are the Section and Mid-Point formulas important in coordinate geometry ? |  |
Ans. The Section and Mid-Point formulas are fundamental in coordinate geometry as they provide essential tools for analyzing and solving problems related to points and lines. These formulas help in determining specific points along a line segment, such as midpoints and points of division, which are crucial for constructing geometric shapes, understanding properties of triangles, and performing transformations. They form the basis for more advanced concepts in geometry and are widely applicable in various fields, including physics, engineering, and computer science.
Related Searches















