Class 10 Exam > Class 10 Notes > Mathematics Class 10 ICSE > Chapter Notes: Equation of A Line
Equation of A Line Chapter Notes | Mathematics Class 10 ICSE PDF Download
Introduction
Dive into the exciting world of coordinate geometry with the "Equation of a Line"! Imagine straight lines as pathways on a graph, each telling a unique story through numbers and equations. This chapter unravels the mysteries of linear equations, slopes, and intercepts, guiding you to master the art of plotting lines, checking points, and understanding their relationships. From the gentle incline of a slope to the thrill of finding a line’s equation, you’ll explore parallel and perpendicular lines, intercepts, and more. Buckle up for a mathematical adventure that transforms the coordinate plane into your playground!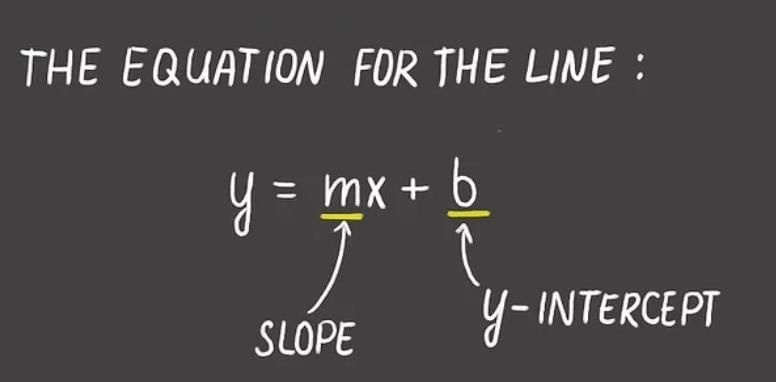
A Basic Concept
- Linear equations involve variables x and y, or just one, and are of the first degree.
- Each linear equation corresponds to a straight line on a graph.
- Every straight line can be described by a linear equation.
- Key points to note:
- A point is on a line if its coordinates fit the line’s equation.
- If a line goes through a point, that point’s coordinates satisfy the equation.
- Example: Check if point (4, -2) lies on the line 3x + 5y = 2.
- Step 1: Insert x = 4 and y = -2 into the equation 3x + 5y = 2.
- Step 2: Calculate: 3 × 4 + 5 × (-2) = 12 - 10 = 2.
- Step 3: Check: 2 = 2, so the equation is true.
- Conclusion: Point (4, -2) lies on the line 3x + 5y = 2.
Inclination of a Line
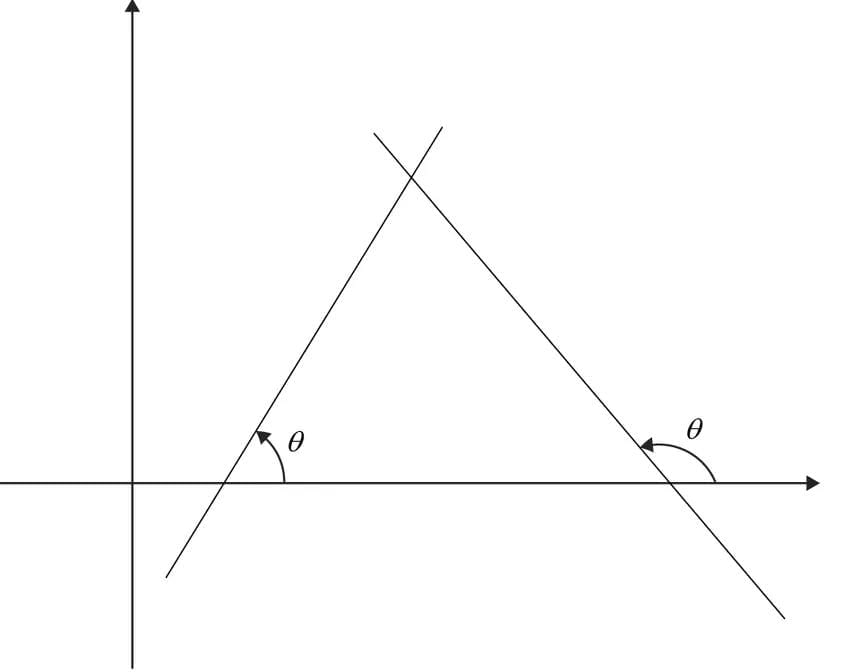
The inclination is the angle a line makes with the positive x-axis.
Steps to grasp inclination:- Counterclockwise measurement makes the angle (θ) positive.
- Clockwise measurement makes the angle (θ) negative.
- The x-axis and lines parallel to it have an inclination of 0°.
- The y-axis and lines parallel to it have an inclination of 90°.
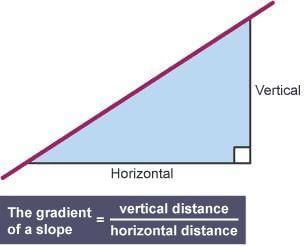
Concept of Slope (or, Gradient)
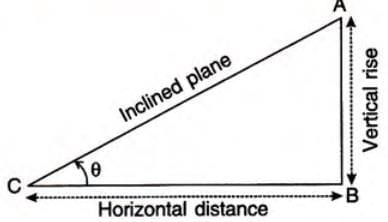
The slope indicates how steep a line is.
Steps to understand slope:
- Think of a line as an inclined plane.
- Slope is the ratio of vertical rise to horizontal distance.
- For a line, slope = vertical rise / horizontal distance.
Formula: Slope of line AC = AB / BC = tan θ, where θ is the angle with the horizontal.
Slope (or, Gradient) of a Straight Line
- The slope, denoted m, is the tangent of a line’s inclination.
- Formula: Slope m = tan θ, where θ is the inclination.
- Slope of the x-axis is 0 (θ = 0°, tan 0° = 0).
- Slope of the y-axis is undefined (θ = 90°, tan 90° is not defined).
- A positive slope means the line makes an acute angle (less than 90°) counterclockwise with the x-axis.
- A negative slope means the line makes an obtuse angle (greater than 90°) counterclockwise or an acute angle clockwise with the x-axis.
- Step 1: Apply the formula: m = tan θ.
- Step 2: Insert θ = 45°.
- Step 3: Calculate: m = tan 45° = 1.
- Conclusion: The slope of the line is 1.
The Slope of a Straight Line Passing Through Two Given Fixed Points
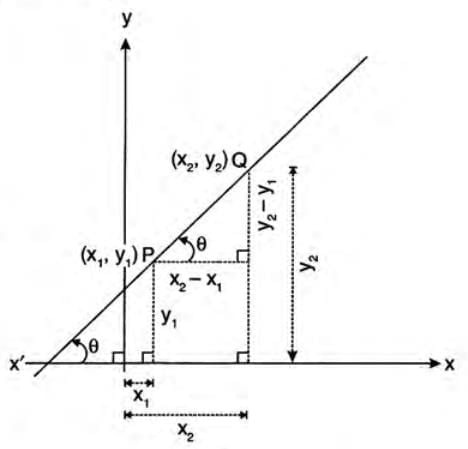
- Find the difference in y-coordinates (ordinates).
- Find the difference in x-coordinates (abscissae).
- Divide the y-difference by the x-difference.
Formula: Slope m = (y2 - y1) / (x2 - x1) or m = (y1 - y2) / (x1 - x2).
Example: Find the slope of the line through A(-2, 3) and B(2, 7).
- Step 1: Label points: A(-2, 3) = (x1, y1) and B(2, 7) = (x2, y2).
- Step 2: Use the formula: m = (y2 - y1) / (x2 - x1).
- Step 3: Substitute: m = (7 - 3) / (2 - (-2)) = 4 / 4 = 1.
- Conclusion: The slope of line AB is 1.
Parallel Lines
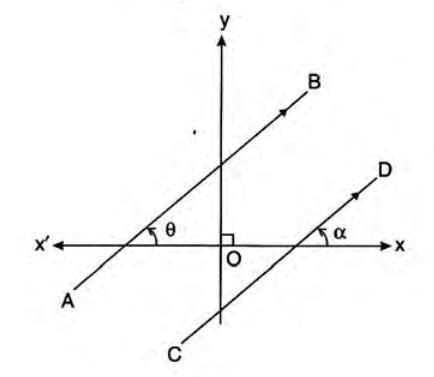
Two lines are parallel if they share the same inclination.
Steps to identify parallel lines:
- Consider lines AB and CD with inclinations θ and α.
- If parallel, then θ = α.
- Thus, tan θ = tan α.
- So, the slope of AB equals the slope of CD.
Property: Parallel lines have equal slopes.
Conversely, if slopes are equal, the lines are parallel.
Perpendicular Lines
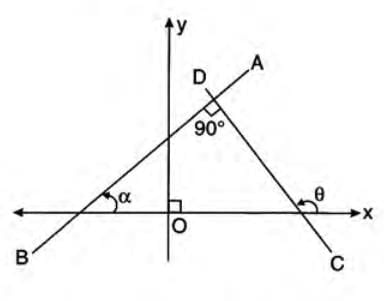
- Two lines are perpendicular if they meet at right angles.
- Steps to understand perpendicularity:
- Let lines AB and CD have inclinations α and θ.
- If perpendicular, then θ = 90° + α.
- Calculate: tan θ = tan (90° + α) = -cot α.
- Since cot α = 1 / tan α, then tan θ = -1 / tan α.
- Thus, tan θ × tan α = -1.
- Formula: If m1 and m2 are slopes of perpendicular lines, then m1 × m2 = -1.
- Conversely, if the product of slopes is -1, the lines are perpendicular.
Condition for Collinearity of Three Points
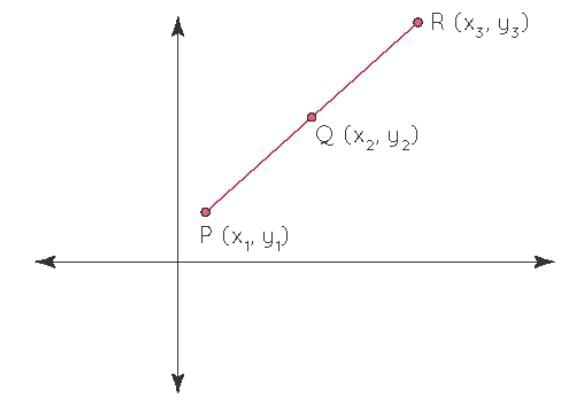Three points A, B, and C are collinear if they lie on one straight line. Condition for collinearity:- Compute the slope of line AB.
- Compute the slope of line BC.
- If the slope of AB equals the slope of BC, points A, B, and C are collinear.
- Step 1: Apply condition: Slope of AB = Slope of BC.
- Step 2: Slope of AB = (0 - 3) / (-5 - 2) = -3 / -7 = 3/7.
- Step 3: Slope of BC = (a - 0) / (-2 - (-5)) = a / 3.
- Step 4: Equate slopes: 3/7 = a / 3.
- Step 5: Solve: a = 9/7 = 1 2/7.
- Conclusion: The value of a is 9/7 or 1 2/7.
X-Intercept
X-Intercept Point
- The x-intercept is the distance from the origin to where a line crosses the x-axis.
- Steps to find the x-intercept:
- Locate point A where the line meets the x-axis.
- The x-intercept is the x-coordinate of point A, i.e., OA.
- If x-intercept is 5, the point on the x-axis is (5, 0).
- If x-intercept is -8, the point on the x-axis is (-8, 0).
Y-Intercept
Y-Intercept Location
- The y-intercept is the distance from the origin to where a line crosses the y-axis.
- Steps to find the y-intercept:
- Locate point where the line meets the y-axis.
- The y-intercept is the y-coordinate of point.
- If y-intercept is 5, the point on the y-axis is (0, 5).
- If y-intercept is -6, the point on the y-axis is (0, -6).
Equation of a Line
A line can be expressed using various equation forms.
Type 1: Slope-Intercept Form
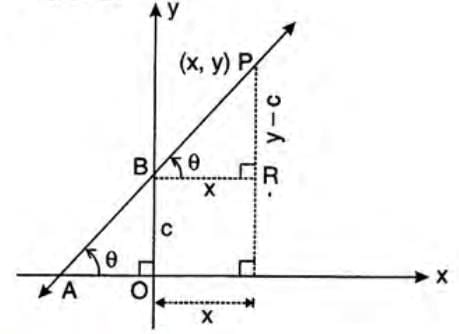Used when slope and y-intercept are known.Steps to derive the equation:
- Consider line AB making angle θ with the x-axis.
- Let y-intercept be c (point B is (0, c)).
- Slope m = tan θ.
- For any point P(x, y) on the line, tan θ = (y - c) / x.
- Rearrange: m x = y - c.
- Final form: y = m x + c.
Formula: y = m x + c, where m is slope and c is y-intercept.
Meaning of c:
- It’s the y-coordinate where the line crosses the y-axis.
- It’s the value of y when x = 0.
- Step 1: Given θ = 45°, so slope m = tan 45° = 1.
- Step 2: Given y-intercept c = 5.
- Step 3: Use slope-intercept form: y = m x + c.
- Step 4: Substitute: y = 1 x + 5.
- Conclusion: The equation is y = x + 5.
Type 2: Point-Slope Form
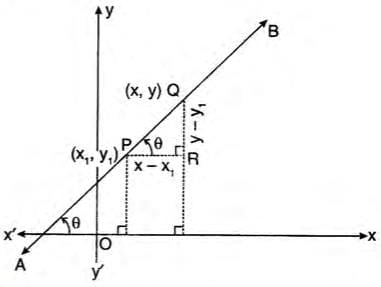Used when slope and a point on the line are known.Steps to derive the equation:- Let line AB have inclination θ and pass through P(x1, y1).
- Slope m = tan θ.
- Consider point Q(x, y) on the line.
- In triangle PQR, (y - y1) / (x - x1) = m.
- Rearrange to form the equation.
Formula: y - y1 = m (x - x1).
Example: Find the equation of a line with inclination 60° and passing through (-2, 5).- Step 1: Given θ = 60°, so slope m = tan 60° = √3.
- Step 2: Given point (x1, y1) = (-2, 5).
- Step 3: Use point-slope form: y - y1 = m (x - x1).
- Step 4: Substitute: y - 5 = √3 (x - (-2)).
- Step 5: Simplify: y - 5 = √3 (x + 2) → y = √3 x + 2√3 + 5.
- Conclusion: The equation is y = √3 x + 2√3 + 5.
Type 3: Two-Points Form
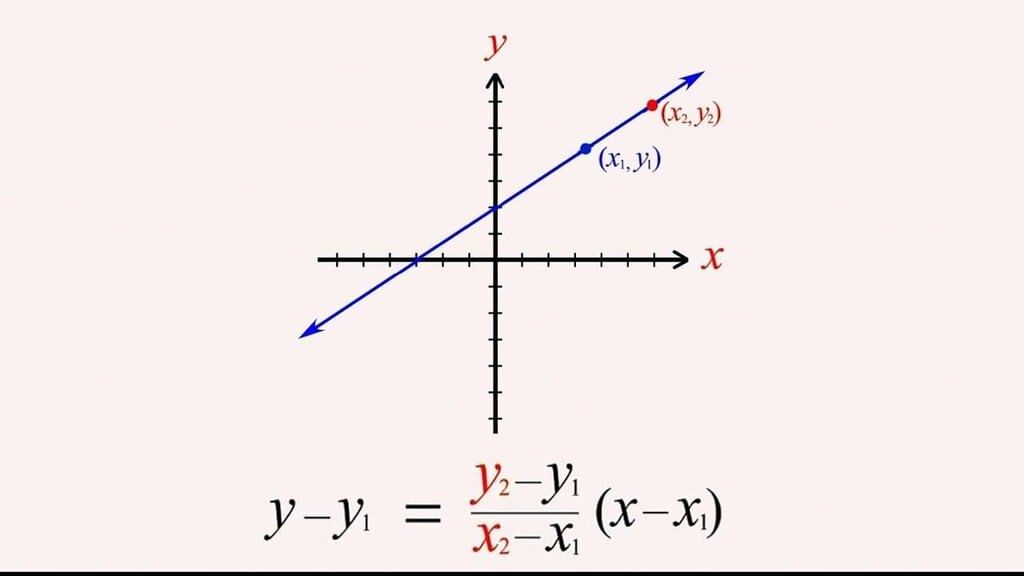
Two-Point Equation
Used when two points on the line are known.
Steps to derive the equation:
- Let the line pass through (x1, y1) and (x2, y2).
- Compute slope: m = (y2 - y1) / (x2 - x1).
- Apply point-slope form with one point.
Formula: y - y1 = m (x - x1), where m = (y2 - y1) / (x2 - x1).
Example: Find the equation of the line through (-3, 1) and (1, 5).- Step 1: Label points: (x1, y1) = (-3, 1), (x2, y2) = (1, 5).
- Step 2: Calculate slope: m = (5 - 1) / (1 - (-3)) = 4 / 4 = 1.
- Step 3: Use point-slope form: y - y1 = m (x - x1).
- Step 4: Substitute: y - 1 = 1 (x - (-3)).
- Step 5: Simplify: y - 1 = x + 3 → y = x + 4.
- Conclusion: The equation is y = x + 4.
Equally Inclined Lines
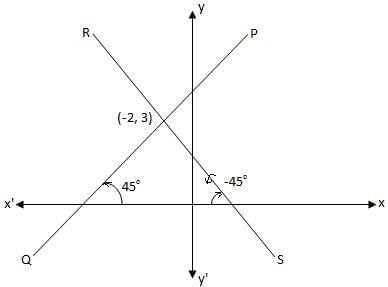
Inclined Lines
Equally inclined lines make equal angles with both x-axis and y-axis.
Steps to understand:
- For line AB, inclination θ = 45°, slope = tan 45° = 1.
- For line CD, inclination θ = -45°, slope = tan (-45°) = -1.
- Step 1: For line AB, slope m = tan 45° = 1, point (x1, y1) = (-2, 3).
- Step 2: Use point-slope form: y - y1 = m (x - x1).
- Step 3: Substitute: y - 3 = 1 (x - (-2)) → y - 3 = x + 2 → y = x + 5.
- Step 4: For line CD, slope m = tan (-45°) = -1, point (x1, y1) = (-2, 3).
- Step 5: Use point-slope form: y - 3 = -1 (x - (-2)) → y - 3 = -x - 2 → x + y = 1.
- Conclusion: Equations are y = x + 5 and x + y = 1.
To Find the Slope and Y-Intercept of a Given Line
Steps to find slope and y-intercept:- Rearrange the equation to the form y = m x + c.
- The coefficient of x is the slope (m).
- The constant term is the y-intercept (c).
- Step 1: Start with 2x - 3y - 4 = 0.
- Step 2: Solve for y: -3y = -2x + 4.
- Step 3: Divide by -3: y = (2/3)x - 4/3.
- Step 4: Identify slope: m = 2/3.
- Step 5: Identify y-intercept: c = -4/3.
- Conclusion: Slope is 2/3, y-intercept is -4/3.
Solved Examples
Example 1: Find the value of k
The line 3x - 8y = 2 passes through (k, 2). Find k.
- Step 1: Substitute x = k and y = 2 into 3x - 8y = 2.
- Step 2: Calculate: 3k - 8 × 2 = 2.
- Step 3: Simplify: 3k - 16 = 2.
- Step 4: Solve: 3k = 18 → k = 6.
- Conclusion: The value of k is 6.
Example 2: Check if a line bisects a segment
Does the line 3x = y + 1 bisect the segment joining A(-2, 3) and B(4, 1)?
- Step 1: Find midpoint of AB: [(x1 + x2)/2, (y1 + y2)/2].
- Step 2: Substitute A(-2, 3) and B(4, 1): [(-2 + 4)/2, (3 + 1)/2] = (1, 2).
- Step 3: Substitute midpoint (1, 2) into 3x = y + 1.
- Step 4: Check: 3 × 1 = 2 + 1 → 3 = 3, which is true.
- Conclusion: The line 3x = y + 1 bisects the segment joining A and B.
Example 3: Find the equation of a line
Find the equation of the line with x-intercept 8 and y-intercept -12.
- Step 1: x-intercept = 8 → point (8, 0).
- Step 2: y-intercept = -12 → point (0, -12).
- Step 3: Calculate slope: m = (y2 - y1) / (x2 - x1) = (-12 - 0) / (0 - 8) = 3/2.
- Step 4: Use point-slope form: y - y1 = m (x - x1).
- Step 5: Substitute: y - 0 = (3/2) (x - 8).
- Step 6: Simplify: 2y = 3x - 24.
- Conclusion: The equation is 2y = 3x - 24.
Example 4: Alternative method for equation of a line
Find the equation of the line through (2, 7) with y-intercept 3.
Method 1:
- Step 1: y-intercept = 3 → point (0, 3).
- Step 2: Given point (x1, y1) = (2, 7), (x2, y2) = (0, 3).
- Step 3: Calculate slope: m = (3 - 7) / (0 - 2) = -4 / -2 = 2.
- Step 4: Use point-slope form: y - y1 = m (x - x1).
- Step 5: Substitute: y - 7 = 2 (x - 2).
- Step 6: Simplify: y - 7 = 2x - 4 → y = 2x + 3.
Alternative Method:
- Step 1: Use slope-intercept form: y = m x + c, where c = 3.
- Step 2: Substitute point (2, 7): 7 = m × 2 + 3.
- Step 3: Solve for m: 7 = 2m + 3 → 2m = 4 → m = 2.
- Step 4: Substitute m and c: y = 2 x + 3.
- Conclusion: The equation is y = 2x + 3.
The document Equation of A Line Chapter Notes | Mathematics Class 10 ICSE is a part of the Class 10 Course Mathematics Class 10 ICSE.
All you need of Class 10 at this link: Class 10
|
74 videos|198 docs|30 tests
|
FAQs on Equation of A Line Chapter Notes - Mathematics Class 10 ICSE
| 1. What is the concept of slope (or gradient) in geometry? |  |
Ans. The slope (or gradient) in geometry refers to the steepness or incline of a line. It is defined as the change in the vertical direction (rise) divided by the change in the horizontal direction (run) between two points on the line. Mathematically, it is expressed as m = (y2 - y1) / (x2 - x1), where (x1, y1) and (x2, y2) are two points on the line.
| 2. How do you calculate the slope of a straight line passing through two fixed points? | |
Ans. To calculate the slope of a straight line passing through two fixed points, you use the formula m = (y2 - y1) / (x2 - x1), where (x1, y1) is the first point and (x2, y2) is the second point. By substituting the coordinates of the two points into the formula, you can determine the slope of the line.
| 3. What is the condition for two lines to be parallel? | |
Ans. Two lines are parallel if they have the same slope. This means that if the slopes of two lines are equal, they will never intersect and will continue indefinitely in the same direction without meeting.
| 4. What does it mean for two lines to be perpendicular? | |
Ans. Two lines are said to be perpendicular if the product of their slopes is equal to -1. This relationship indicates that the lines intersect at a right angle (90 degrees). For example, if one line has a slope of m1, the other line will have a slope of m2 such that m1 * m2 = -1.
| 5. How can you determine the x-intercept of a line given its equation? | |
Ans. The x-intercept of a line can be determined by setting the y-coordinate to zero in the equation of the line and solving for x. For example, in the equation y = mx + b, you would set y = 0, leading to the equation 0 = mx + b. Solving this for x gives you the x-intercept.
About this Document
4.60/5
Rating
Sep 30, 2025
Last updated
Related Exams
Document Description: Chapter Notes: Equation of A Line for Class 10 2025 is part of Mathematics Class 10 ICSE preparation.
The notes and questions for Chapter Notes: Equation of A Line have been prepared according to the Class 10 exam syllabus. Information about Chapter Notes: Equation of A Line covers topics
like Introduction, A Basic Concept, Inclination of a Line, Concept of Slope (or, Gradient), Slope (or, Gradient) of a Straight Line, The Slope of a Straight Line Passing Through Two Given Fixed Points, Parallel Lines, Perpendicular Lines, Condition for Collinearity of Three Points, X-Intercept, Y-Intercept, Equation of a Line, Equally Inclined Lines, To Find the Slope and Y-Intercept of a Given Line and Chapter Notes: Equation of A Line Example, for Class 10 2025 Exam. Find important definitions, questions, notes, meanings, examples, exercises and tests below for Chapter Notes: Equation of A Line.
Introduction of Chapter Notes: Equation of A Line in English is available as part of our Mathematics Class 10 ICSE
for Class 10 & Chapter Notes: Equation of A Line in Hindi for Mathematics Class 10 ICSE course.
Download more important topics related with notes, lectures and mock test series for Class 10
Exam by signing up for free. Class 10: Equation of A Line Chapter Notes | Mathematics Class 10 ICSE
Description
Full syllabus notes, lecture & questions for Equation of A Line Chapter Notes | Mathematics Class 10 ICSE - Class 10 | Plus excerises question with solution to help you revise complete syllabus for Mathematics Class 10 ICSE | Best notes, free PDF download
Information about Chapter Notes: Equation of A Line
In this doc you can find the meaning of Chapter Notes: Equation of A Line defined & explained in the simplest way possible. Besides explaining types of
Chapter Notes: Equation of A Line theory, EduRev gives you an ample number of questions to practice Chapter Notes: Equation of A Line tests, examples and also practice Class 10
tests
Related Searches
Sample Paper
,ppt
,Semester Notes
,past year papers
,Equation of A Line Chapter Notes | Mathematics Class 10 ICSE
,Free
,Equation of A Line Chapter Notes | Mathematics Class 10 ICSE
,video lectures
,Important questions
,Viva Questions
,Exam
,study material
,practice quizzes
,Extra Questions
,Summary
,Equation of A Line Chapter Notes | Mathematics Class 10 ICSE
,Objective type Questions
,shortcuts and tricks
,mock tests for examination
,Previous Year Questions with Solutions
,MCQs
;
Additional Information about Chapter Notes: Equation of A Line for Class 10 Preparation
Chapter Notes: Equation of A Line Free PDF Download
The Chapter Notes: Equation of A Line is an invaluable resource that delves deep into the core of the Class 10 exam.
These study notes are curated by experts and cover all the essential topics and concepts, making your preparation more efficient and effective.
With the help of these notes, you can grasp complex subjects quickly, revise important points easily,
and reinforce your understanding of key concepts. The study notes are presented in a concise and easy-to-understand manner,
allowing you to optimize your learning process. Whether you're looking for best-recommended books, sample papers, study material,
or toppers' notes, this PDF has got you covered. Download the Chapter Notes: Equation of A Line now and kickstart your journey towards success in the Class 10 exam.
Importance of Chapter Notes: Equation of A Line
The importance of Chapter Notes: Equation of A Line cannot be overstated, especially for Class 10 aspirants.
This document holds the key to success in the Class 10 exam.
It offers a detailed understanding of the concept, providing invaluable insights into the topic.
By knowing the concepts well in advance, students can plan their preparation effectively.
Utilize this indispensable guide for a well-rounded preparation and achieve your desired results.
Chapter Notes: Equation of A Line
Chapter Notes: Equation of A Line Notes offer in-depth insights into the specific topic to help you master it with ease.
This comprehensive document covers all aspects related to Chapter Notes: Equation of A Line.
It includes detailed information about the exam syllabus, recommended books, and study materials for a well-rounded preparation.
Practice papers and question papers enable you to assess your progress effectively.
Additionally, the paper analysis provides valuable tips for tackling the exam strategically.
Access to Toppers' notes gives you an edge in understanding complex concepts.
Whether you're a beginner or aiming for advanced proficiency, Chapter Notes: Equation of A Line Notes on EduRev are your ultimate resource for success.
Chapter Notes: Equation of A Line Class 10 Questions
The "Chapter Notes: Equation of A Line Class 10 Questions" guide is a valuable resource for all aspiring students preparing for the
Class 10 exam. It focuses on providing a wide range of practice questions to help students gauge
their understanding of the exam topics. These questions cover the entire syllabus, ensuring comprehensive preparation.
The guide includes previous years' question papers for students to familiarize themselves with the exam's format and difficulty level.
Additionally, it offers subject-specific question banks, allowing students to focus on weak areas and improve their performance.
Study Chapter Notes: Equation of A Line on the App
Students of Class 10 can study Chapter Notes: Equation of A Line alongwith tests & analysis from the EduRev app,
which will help them while preparing for their exam. Apart from the Chapter Notes: Equation of A Line,
students can also utilize the EduRev App for other study materials such as previous year question papers, syllabus, important questions, etc.
The EduRev App will make your learning easier as you can access it from anywhere you want.
The content of Chapter Notes: Equation of A Line is prepared as per the latest Class 10 syllabus.
|
© EduRev
|
Education Revolution
|
|
Signup to see your scores
go up within 7 days!
Access 1000+ FREE Docs, Videos and Tests
Takes less than 10 seconds to signup