Loci Chapter Notes | Mathematics Class 10 ICSE PDF Download
| Table of contents |

|
| Introduction |

|
| Locus and Its Constructions |

|
| Theorems Based on Symmetry |

|
| Applications |

|
| Summary |

|
Introduction
Imagine a point moving through space, tracing a path as it follows specific rules—like staying the same distance from two lines or circling around a fixed point! This fascinating concept is called a locus, and in this chapter, we dive into the exciting world of loci and their constructions. From straight lines to circles, we'll explore how points move to create unique shapes based on given conditions. Get ready to uncover the secrets of loci, understand their properties, and learn how to construct them step by step using rulers and compasses. Let’s embark on this geometric adventure and see how loci bring mathematics to life!
Locus and Its Constructions

- Origin of the term: The word "locus" comes from Latin, related to words like "location" and "locality."
- Definition: A locus is the path a point traces as it moves to satisfy specific conditions.
Example: Two parallel lines l and s are 4 cm apart. Find the locus of a point always equidistant from both lines.
- Step 1: Understand the condition—the point must be at the same distance from both lines.
- Step 2: Since the lines are 4 cm apart, the point is 4/2 = 2 cm from each line.
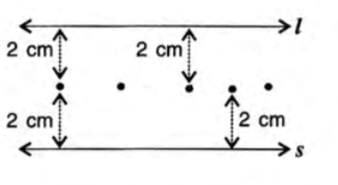
- Step 3: Mark points 2 cm from line l and 2 cm from line s.
- Step 4: Join these points to form a straight line, labeled AB.
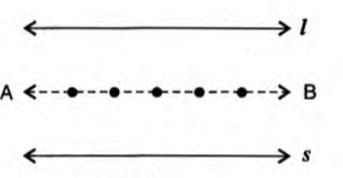
- Result: The locus is line AB, parallel to both l and s, and equidistant from them.
Process:
- Step 1: Identify the condition the moving point must satisfy.
- Step 2: Mark points that follow this condition.
- Step 3: Connect the points to trace the path, which could be a line, curve, or circle.
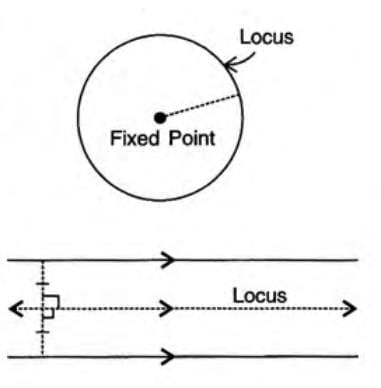
Example: Show the locus of a point equidistant from a fixed point is a circle with the fixed point as the center.
- Step 1: Let O be the fixed point, and P be the moving point.
- Step 2: Condition—distance OP is always constant, say r cm.
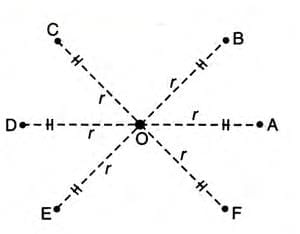
- Step 3: Mark points A, B, C, D, E, etc., each r cm from O.
- Step 4: Draw a smooth curve through these points.
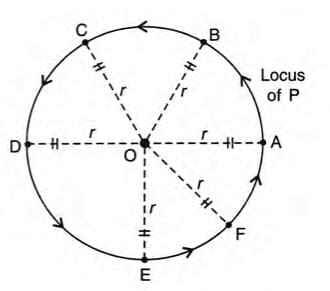
- Result: The locus is a circle with center O and radius r.
Theorems Based on Symmetry
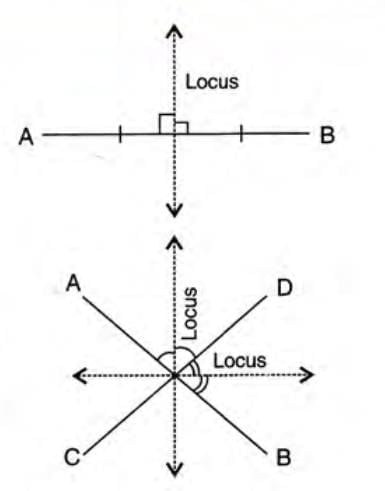
Theorem 3: The locus of a point equidistant from two intersecting lines is the bisector of the angles between them.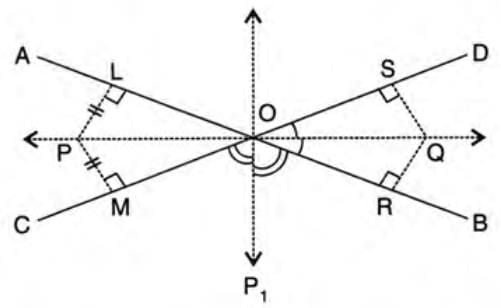
Steps to understand:
- Step 1: Consider two lines AB and CD intersecting at point O.
- Step 2: A point P is equidistant from AB and CD.
- Step 3: Draw PL perpendicular to AB and PM perpendicular to CD.
- Step 4: In triangles POL and POM, PL = PM (given), ∠PLO = ∠PMO = 90°, and PO is common.
- Step 5: Triangles are congruent by RHS (Right angle-Hypotenuse-Side).
- Step 6: Thus, ∠POL = ∠POM, so P lies on the angle bisector of ∠AOC.
- Step 7: Conversely, any point Q on the bisector is equidistant from AB and CD (prove using congruent triangles OQR and OQS by AAS or ASA).
Theorem 4: The locus of a point equidistant from two fixed points is the perpendicular bisector of the line joining them.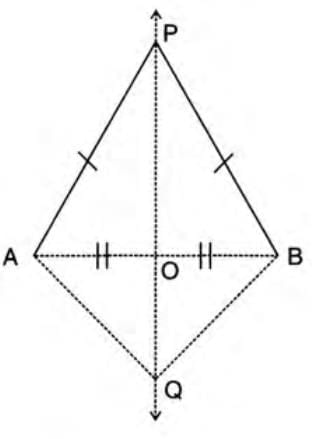 Steps to understand:
Steps to understand:
- Step 1: Take fixed points A and B, and a moving point P where PA = PB.
- Step 2: Find O, the midpoint of AB, and join P to O.
- Step 3: In triangles AOP and BOP, PA = PB (given), AO = BO (midpoint), and PO is common.
- Step 4: Triangles are congruent by SSS (Side-Side-Side).
- Step 5: Thus, ∠AOP = ∠BOP = 90°, so P lies on the perpendicular bisector of AB.
- Step 6: Conversely, any point Q on the perpendicular bisector is equidistant from A and B (prove using congruent triangles AOQ and BOQ by SAS).
Applications
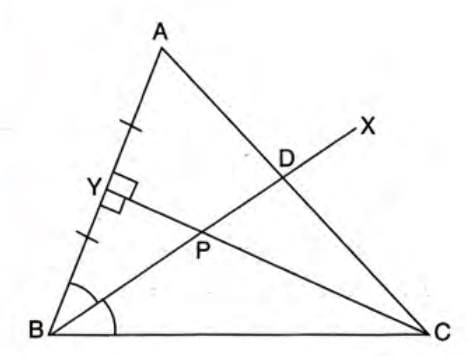
Concept: Loci are used to find points satisfying specific geometric conditions in triangles, quadrilaterals, etc.
Steps to apply:
- Step 1: Understand the given figure and conditions.
- Step 2: Use properties like angle bisectors, perpendicular bisectors, or parallel lines.
- Step 3: Construct the locus by marking points or drawing lines.
- Step 4: Prove the locus using congruent triangles or symmetry.
Example: In triangle ABC, BX bisects ∠ABC and intersects AC at D. Line CY is perpendicular to AB and intersects BX at P, where Y is the midpoint of AB. Prove: (i) P is equidistant from A and B, (ii) D is equidistant from AB and BC.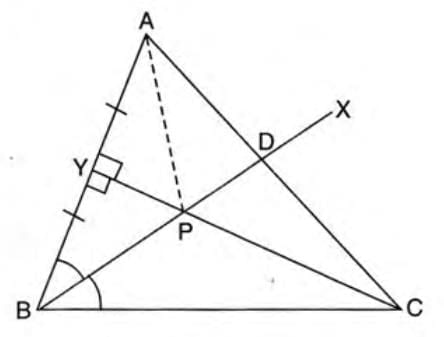
- Join A and P.
- In triangles APY and BPY:
- AY = BY (Y is midpoint).
- PY is common.
- ∠AYP = ∠BYP = 90° (CY is perpendicular to AB).
- Triangles are congruent by SAS.
- Thus, AP = BP, so P is equidistant from A and B.
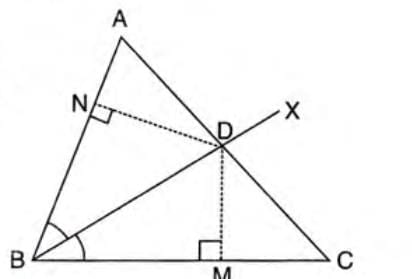
- Draw DM perpendicular to BC, DN perpendicular to BA.
- In triangles DBM and DBN:
- BD is common.
- ∠DBM = ∠DBN (BX bisects ∠ABC).
- ∠DMB = ∠DNB = 90°.
- Triangles are congruent by AAS.
- Thus, DM = DN, so D is equidistant from AB and BC.
Summary
- Locus of a point equidistant from two fixed points: The perpendicular bisector of the line segment joining them.
- Locus of a point equidistant from two intersecting lines: A pair of straight lines that bisect the angles between the given lines.
- Locus of a point at a fixed distance from a given point: The circumference of a circle with the given point as center and the fixed distance as radius.
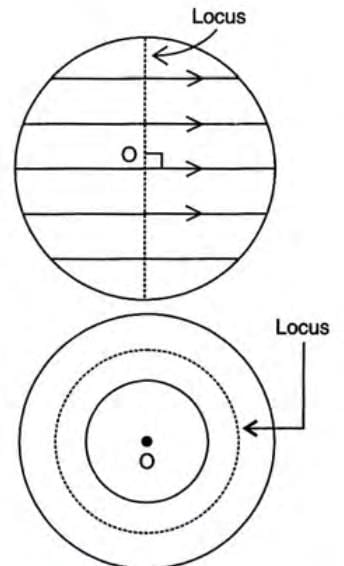
- Locus of a point equidistant from two parallel lines: A line parallel to both and midway between them.
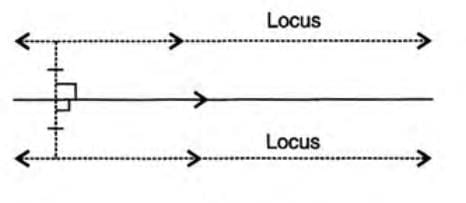
- Locus of a point at a given distance from a line: A pair of lines parallel to the given line, at the given distance on either side.
- Locus of midpoints of equal chords in a circle: The circumference of a circle concentric with the given circle, with radius equal to the distance of the chords from the center.
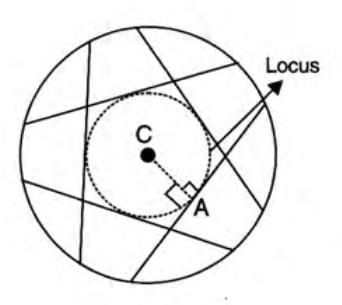
- Locus of midpoints of parallel chords in a circle: The diameter of the circle perpendicular to the parallel chords.
- Locus of a point equidistant from two concentric circles: The circumference of a circle concentric with them, midway between them.
Example: A and B are two fixed points. Draw the locus of point P such that ∠APB = 90°.
- Step 1: Join A and B.
- Step 2: Draw a circle with AB as the diameter.
- Step 3: The locus of point P is the circumference of this circle.
- Reason: The angle in a semicircle is always 90°, so ∠APB = 90° for any point P on the circle.
Important
Centroid: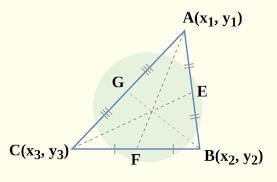 Centroid Properties
Centroid Properties
- Definition: The point where the three medians of a triangle intersect.
- Property: Divides each median in the ratio 2:1.
- Example: In triangle ABC, medians AP, BQ, and CR intersect at G, the centroid.
- Formula: AG : GP = 2:1, BG : GQ = 2:1, CG : GR = 2:1.
Incentre: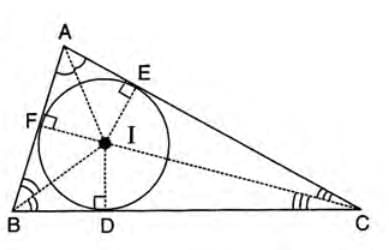
- Definition: The point where the angle bisectors of a triangle intersect.
- Property: Equidistant from all three sides of the triangle.
- Example: In triangle ABC, angle bisectors AI, BI, and CI meet at I, the incentre.
- Property: ID = IE = IF, where D, E, F are points of contact with sides BC, CA, AB.
Circumcentre: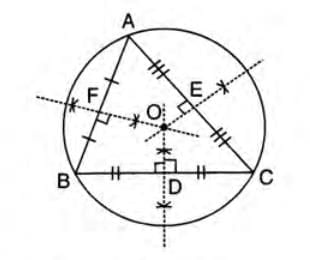
- Definition: The point where the perpendicular bisectors of the three sides of a triangle intersect.
- Property: Equidistant from the vertices A, B, and C.
- Example: In triangle ABC, perpendicular bisectors DO, EO, and FO of sides BC, CA, and AB meet at O.
- Formula: OA = OB = OC, the radius of the circumcircle.
Orthocentre: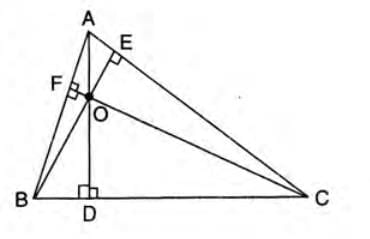
- Definition: The point where the altitudes from the vertices to the opposite sides intersect.
- Example: In triangle ABC, altitudes AD, BE, and CF from vertices A, B, C to sides BC, CA, AB meet at O, the orthocentre.
Isosceles Triangle Properties: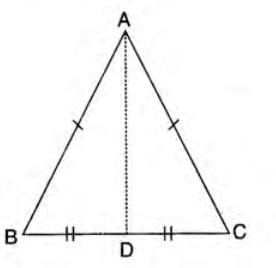
- In triangle ABC, if AD is the median to base BC:
- AD is also the angle bisector of ∠A.
- AD is the perpendicular bisector of BC.
- AD is the altitude from A to BC.
Equilateral Triangle Properties: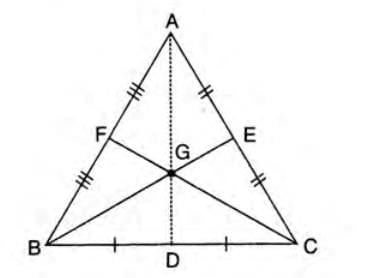
- In equilateral triangle ABC:
- Median AD = angle bisector of ∠A = perpendicular bisector of BC = altitude to BC.
- Median BE = angle bisector of ∠B = perpendicular bisector of AC = altitude to AC.
- Median CF = angle bisector of ∠C = perpendicular bisector of AB = altitude to AB.
- Centroid G = incentre = circumcentre = orthocentre.
Example:
- Concept: In triangle ABC, AP, BQ, and CR are medians intersecting at G.
- Property: G is the centroid, dividing each median in the ratio 2:1.
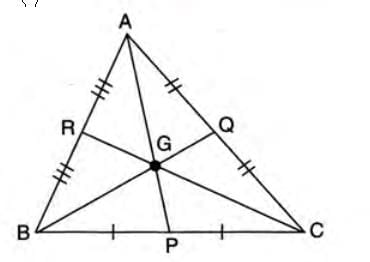
- Result: AG : GP = 2:1, BG : GQ = 2:1, CG : GR = 2:1.
|
74 videos|328 docs|30 tests
|
FAQs on Loci Chapter Notes - Mathematics Class 10 ICSE
| 1. What is the definition of a locus in geometry? |  |
| 2. What are some key theorems based on symmetry in relation to loci? |  |
| 3. How can loci be applied in real-life situations? |  |
| 4. What are some common constructions involving loci? |  |
| 5. What is the importance of studying loci in Class 10 mathematics? |  |




















