Constructions Chapter Notes | Mathematics Class 10 ICSE PDF Download
| Table of contents |

|
| Introduction |

|
| Construction of Tangents to a Given Circle |

|
| Construction of Circumscribed and Inscribed Circles of a Triangle |

|
| Circumscribing and Inscribing a Circle on Regular Hexagon |

|
Introduction
Circles have fascinated mathematicians for centuries due to their perfect symmetry and unique properties. In this chapter, we dive into the exciting world of geometric constructions related to circles, where we use only a ruler and compass to create precise figures like tangents, circumscribed circles, and inscribed circles. These constructions are not just about drawing shapes but understanding the deep relationships between points, lines, and circles in geometry. Whether it’s finding the perfect tangent to a circle or inscribing a circle within a triangle, this chapter equips you with the skills to construct these figures step-by-step, making geometry both fun and logical!
Construction of Tangents to a Given Circle
Let’s explore how to construct tangents to a circle, either from a point on its circumference or from an external point. A tangent is a line that touches the circle at exactly one point, and these constructions rely on the geometric property that the angle between the radius and the tangent at the point of contact is always 90°.
Construction 1: Tangent to a Circle Through a Point on Its Circumference
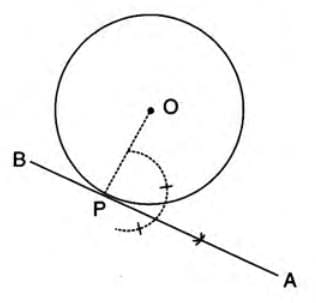
- Identify the center of the circle as O and a point P on the circle’s circumference.
- Connect point O to point P with a straight line (radius OP).
- At point P, draw a line APB such that it forms a 90° angle with OP (i.e., ∠OPA = 90°).
- The line APB is the required tangent, touching the circle at point P.
Construction 2: Tangents to a Circle from an Exterior Point
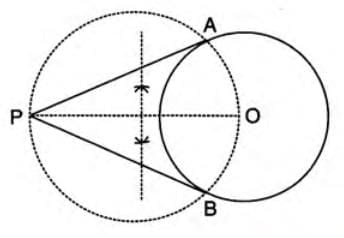
- Identify the center of the circle as O and an exterior point P outside the circle.
- Draw a line connecting points P and O.
- Construct a circle with OP as the diameter, which intersects the given circle at points A and B.
- Draw lines PA and PB from point P to points A and B, respectively.
- PA and PB are the two tangents from point P to the circle.
- Verify that the lengths of tangents PA and PB are equal (PA = PB).
- Tangents from an exterior point to a circle are equal in length: PA = PB.
- The angle at the point of contact is 90°: ∠PAO = 90° and ∠PBO = 90°.
- By Pythagoras Theorem: PA2 + OA2 = OP2, so PA = √(OP2 - OA2) = PB.
Construction of Circumscribed and Inscribed Circles of a Triangle
This section focuses on constructing circles that either pass through the vertices of a triangle (circumscribed) or touch all three sides (inscribed). These constructions highlight the roles of the circumcentre and incentre of a triangle.
Construction 3: Circumscribing Circle of a Triangle
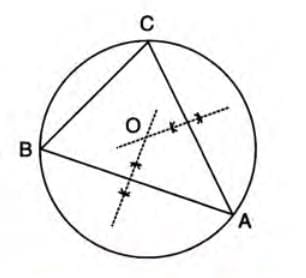
- Take a triangle ABC and draw the perpendicular bisectors of any two sides (e.g., AB and AC).
- Find the point where these perpendicular bisectors intersect, and label it O (the circumcentre).
- Using O as the center and the distance OA (or OB or OC) as the radius, draw a circle.
- This circle passes through all three vertices A, B, and C of the triangle.
- The perpendicular bisectors of a triangle’s sides are concurrent, meeting at the circumcentre O.
- The circumcentre O is equidistant from the vertices: OA = OB = OC (circumradius).
Construction 4: Inscribed Circle of a Triangle
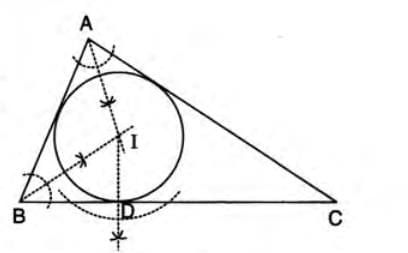
- Take a triangle ABC and draw the angle bisectors of any two angles (e.g., ∠A and ∠B).
- Find the point where these angle bisectors intersect, and label it I (the incentre).
- From point I, draw a perpendicular line ID to any side of the triangle (e.g., BC).
- Using I as the center and ID as the radius, draw a circle that touches all three sides of the triangle.
- The angle bisectors of a triangle are concurrent, meeting at the incentre I.
- The incentre I is equidistant from all three sides of the triangle.
Additional Note
The methods for constructing circumscribed and inscribed circles apply to all triangles, whether regular (equilateral) or irregular.
Circumscribing and Inscribing a Circle on Regular Hexagon
Regular hexagons, with their equal sides and angles, allow for straightforward circle constructions. We can construct both circumscribed and inscribed circles using perpendicular bisectors and angle bisectors, respectively.
Construction 5: Circumscribing Circle of a Regular Hexagon
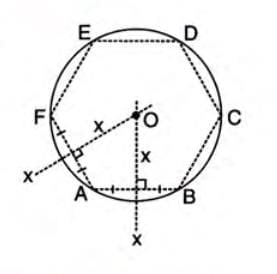
- Construct a regular hexagon ABCDEF with a given side length (e.g., 4 cm).
- Draw the perpendicular bisectors of any two sides (e.g., AB and AF), which intersect at point O.
- Using O as the center and OA as the radius, draw a circle that passes through all vertices of the hexagon.
- Formula for Interior Angle of a Regular Hexagon:
Interior angle = [(2n - 4) / n] × 90°, where n = 6 (number of sides).
= [(2 × 6 - 4) / 6] × 90° = 120°.
Alternative Method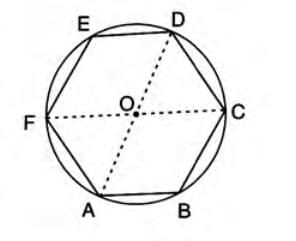
- Construct the regular hexagon ABCDEF with side length 4 cm.
- Draw two main diagonals (e.g., AD and FC), which intersect at point O.
- Using O as the center and OA as the radius, draw a circle passing through all vertices.
- Note: For a regular hexagon, the radius of the circumcircle equals the side length (e.g., 4 cm).
Construction 6: Inscribing Circle of a Regular Hexagon
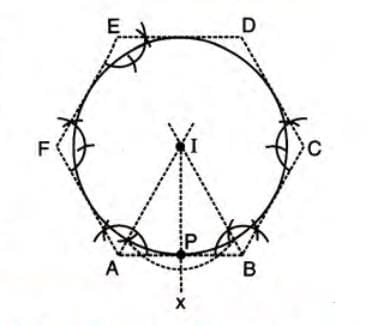
- Construct a regular hexagon ABCDEF with a given side length (e.g., 4.6 cm).
- Draw the angle bisectors of any two interior angles (e.g., at A and B), which intersect at point I.
- From point I, draw a perpendicular IP to any side (e.g., AB).
- Using I as the center and IP as the radius, draw a circle that touches all six sides of the hexagon.
- Formula for Interior Angle of a Regular Hexagon:
Interior angle = [(2 × 6 - 4) / 6] × 90° = 120°.
Additional Note
If the hexagon is not regular, it may not always be possible to construct a circumscribed or inscribed circle.
Solved Examples
- Draw a circle with center O and radius 3 cm.
- Mark point P 5 cm from O.
- Join OP and draw a circle with OP as diameter, intersecting the original circle at A and B.
- Draw lines PA and PB (tangents).
- Measure PA and PB; they should be equal, approximately √(52 - 32) = √16 = 4 cm.
- Draw an equilateral triangle ABC with each side 4.5 cm.
- Construct perpendicular bisectors of sides AB and AC, intersecting at O.
- With O as center and OA as radius, draw the circumcircle.
- Measure the radius (approximately 4.5 cm, as the circumradius of an equilateral triangle is side/√3 ≈ 2.6 cm).
- Draw a regular hexagon ABCDEF with side 4 cm.
- Draw perpendicular bisectors of sides AB and AF, intersecting at O.
- With O as center and OA (4 cm) as radius, draw the circumcircle.
- Alternatively, draw diagonals AD and FC to find O, then draw the circle with radius 4 cm.
|
74 videos|213 docs|30 tests
|
FAQs on Constructions Chapter Notes - Mathematics Class 10 ICSE
| 1. What are the steps to construct a tangent to a given circle? |  |
| 2. How can we construct the circumscribed circle of a triangle? |  |
| 3. What is the method to inscribe a circle within a triangle? |  |
| 4. How can we circumscribe and inscribe a circle on a regular hexagon? |  |
| 5. What are the applications of circle constructions in geometry? |  |














