Trigonometrical Identities Chapter Notes | Mathematics Class 10 ICSE PDF Download
Introduction
Trigonometry is like a treasure map for understanding triangles! It’s a fascinating branch of mathematics that unlocks the secrets of angles and sides, helping us measure and explore the world around us. Whether you're figuring out the height of a tree or the angle of a rocket's trajectory, trigonometry is your trusty guide. In this chapter, we dive into the exciting world of trigonometrical identities, complementary angles, and the use of four-figure tables to make calculations a breeze. Let’s embark on this mathematical adventure with enthusiasm!
Trigonometry
- Trigonometry is the study of measuring triangles, focusing on the relationships between their sides and angles.
- It helps us calculate unknown sides or angles in triangles, especially right-angled ones.
- Example: In a right-angled triangle, if you know one angle and one side, trigonometry can help find the other sides or angles.
Trigonometrical Ratios
- Trigonometrical ratios are special ratios that connect the sides of a right-angled triangle to its acute angles.
- There are six main ratios: sine (sin), cosine (cos), tangent (tan), cotangent (cot), secant (sec), and cosecant (cosec).
- These ratios are defined for an acute angle A in a right-angled triangle with sides labeled as:
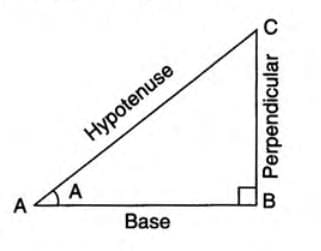
- Perpendicular (BC): The side opposite to angle A.
- Base (AB): The side adjacent to angle A.
- Hypotenuse (AC): The longest side, opposite the right angle.
- Formulas:
- sin A = Perpendicular / Hypotenuse = BC / AC
- cos A = Base / Hypotenuse = AB / AC
- tan A = Perpendicular / Base = BC / AB
- cot A = Base / Perpendicular = AB / BC
- sec A = Hypotenuse / Base = AC / AB
- cosec A = Hypotenuse / Perpendicular = AC / BC
- Key points:
- Each ratio is a unitless real number.
- The value of a ratio remains constant for a given angle, regardless of the triangle’s size.
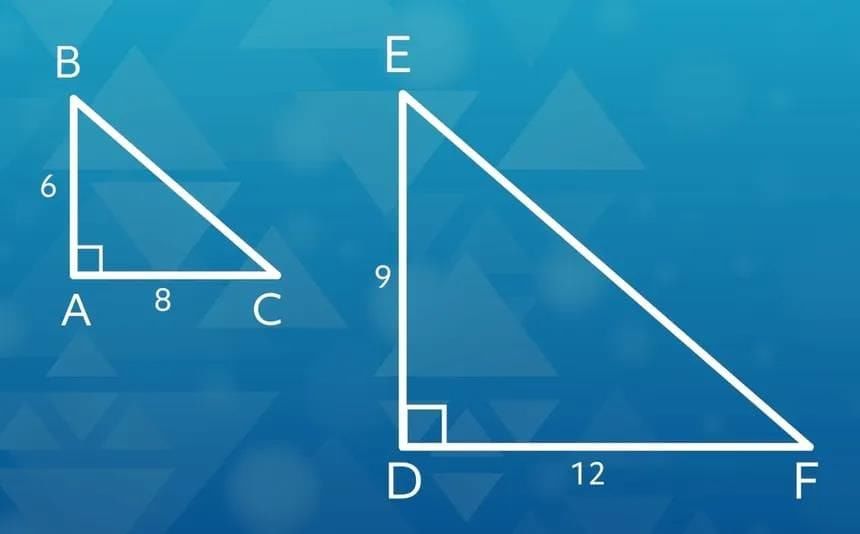
- Example: In triangle BAC, if angle C is equal to angle F in triangle EDF, then sin C = Sin F = BA / BC = ED/ EF, showing that the sine of equal angles is consistent across different triangles.
Relations Between Different Trigonometrical Ratios
Trigonometrical ratios are interconnected through specific relationships: reciprocal, quotient, and square relations.
1. Reciprocal Relations
- Some ratios are inverses of each other.
- Formulas:
- sin A = 1 / cosec A and cosec A = 1 / sin A
- cos A = 1 / sec A and sec A = 1 / cos A
- tan A = 1 / cot A and cot A = 1 / tan A
- Example: If sin A = 0.5, then cosec A = 1 / 0.5 = 2.
2. Quotient Relations
- These show how sine and cosine relate to tangent and cotangent.
- Formulas:
- tan A = sin A / cos A
- cot A = cos A / sin A
- Example: If sin A = 3/5 and cos A = 4/5, then tan A = sin A / cos A = (3/5) / (4/5) = 3/4.
3. Square Relations
- These relations use the Pythagorean theorem to connect the ratios.
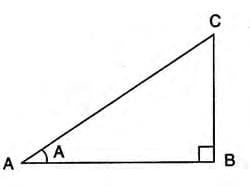
- Formulas:
- sin2 A + cos2 A = 1
- 1 + tan2 A = sec2 A
- 1 + cot2 A = cosec2 A
- Derived forms:
- sin2 A = 1 - cos2 A
- cos2 A = 1 - sin2 A
- sec2 A - tan2 A = 1
- sec2 A - 1 = tan2 A
- cosec2 A - cot2 A = 1
- cosec2 A - 1 = cot2 A
- Example: In triangle ABC, sin A = BC / AC, cos A = AB / AC. Using Pythagorean theorem (AB2 + BC2 = AC2), we get sin2 A + cos2 A = (BC2 + AB2) / AC2 = AC2 / AC2 = 1.
Trigonometric Identities
- A trigonometric identity is an equation involving trigonometric ratios that holds true for all values of the angle.
- Reciprocal, quotient, and square relations are examples of identities.
- To prove an identity:
- Start with the more complex side (LHS or RHS).
- Use known trigonometric relations to simplify it to match the other side.
- If both sides are complex, simplify both independently to a common result.
Example: Prove tan A + cot A = sec A · cosec A
- LHS = tan A + cot A = (sin A / cos A) + (cos A / sin A)
- = (sin2 A + cos2 A) / (cos A · sin A) = 1 / (cos A · sin A)
- = (1 / cos A) · (1 / sin A) = sec A · cosec A = RHS
- Example: Prove cos4 A - sin4 A = 2 cos2A - 1
- LHS = (cos2 A)2 - (sin2 A)2 = (cos2 A - sin2 A)(cos2 A + sin2 A)
- = (cos2 A - sin2 A) · 1 = cos2 A - (1 - cos2 A)
- = cos2 A - 1 + cos2 A = 2 cos2 A - 1 = RHS
Example: Prove (1 + cot A)2+ (1 - ascend desc="Example: Prove sin A / (1 + cos A) + (1 + cos A) / sin A = 2 cosec A
- LHS = [sin2 A + (1 + cos A)2] / [(1 + cos A) sin A]
- = [sin2 A + 1 + cos2 A + 2 cos A] / [(1 + cos A) sin A]
- = [1 + 2 cos A] / [(1 + cos A) sin A] = 2 / sin A = 2 cosec A = RHS
- Alternative method for (1 + cot A)2 + (1 - cot A)2 = 2 cosec2A:
- LHS = 1 + cot2 A + 2 cot A + 1 + cot2 A - 2 cot A
- = 2 + 2 cot2 A = 2 (1 + cot2 A) = 2 cosec2 A = RHS
Trigonometrical Ratios of Complementary Angles
- Complementary angles sum to 90° (e.g., A and 90° - A).
- The trigonometric ratios of complementary angles are related.
- Formulas:
- sin (90° - A) = cos A
- cos (90° - A) = sin A
- tan (90° - A) = cot A
- cot (90° - A) = tan A
- sec (90° - A) = cosec A
- cosec (90° - A) = sec A
Example: Given cos 38° sec (90° - 2A) = 1, find A.
- cos 38° sec (90° - 2A) = 1
- sec (90° - 2A) = cosec 2A, so cos 38° · (1 / sin 2A) = 1
- sin 2A = cos 38° = cos (90° - 52°) = sin 52°
- Thus, 2A = 52°, so A = 26°.
Using the Trigonometrical Tables
- Trigonometrical tables provide values of sine, cosine, and tangent for angles to four decimal places.
- Table structure:
- Left column: degrees from 0° to 89°.
- Middle columns: minutes (0’, 6’, 12’, ..., 54’).
- Right columns: additional minutes (1’, 2’, 3’, 4’, 5’).
- Note: 1° = 60 minutes (60’).
- Example: To find a ratio (e.g., sin 36° 51’):

- Locate the closest lower angle (36° 48’ = 0.5990).
- Add the difference for 3’ (0.0007).
- Result: sin 36° 51’ = 0.5990 + 0.0007 = 0.5997.
- Example: To find an angle given a ratio (e.g., sin θ = 0.5798):

- Find the angle with a sine just below 0.5798 (e.g., sin 35° 24’ = 0.5793).
- Calculate difference (0.5798 - 0.5793 = 0.0005).
- Find minutes corresponding to 0.0005 (2’).
- Result: θ = 35° 24’ + 2’ = 35° 26’.
|
74 videos|198 docs|30 tests
|
FAQs on Trigonometrical Identities Chapter Notes - Mathematics Class 10 ICSE
| 1. What are the basic trigonometric ratios, and how are they defined in a right-angled triangle? |  |
| 2. How do trigonometric identities help in solving trigonometric equations? |  |
| 3. What are the trigonometric ratios of complementary angles? |  |
| 4. How can trigonometric tables be used in calculations? |  |
| 5. What is the significance of trigonometric identities in real-world applications? |  |















