Measures of Central Tendency Chapter Notes | Mathematics Class 10 ICSE PDF Download
Introduction
Imagine you're trying to summarize a big pile of data, like the heights of all students in your school or the scores in a class test. Measures of central tendency are like the "middle ground" that help us describe the typical or central value in such data sets. These measures give us a single number that represents the whole group, making it easier to understand and compare data. They are designed to capture the essence of the data by focusing on a value that's neither too high nor too low but somewhere in the middle where most data points tend to cluster. This chapter dives into four key measures: mean, median, quartiles, and mode, each offering a unique way to summarize data!
- Measures of central tendency are numerical values that represent the characteristics of a large data set.
- They provide a central value that lies between the highest and lowest values, often where most data points are concentrated.
- The chapter covers:
- Arithmetic Mean
- Median
- Mode
- Quartiles
Arithmetic Mean
- The arithmetic mean, or simply mean, is the sum of all numbers in a set divided by the count of numbers.
- It represents the average value of the data set.
- Formula: Mean = (x1 + x2 + x3 + ... + xn) / n = Σx / n,
- where Σ (sigma) denotes the sum of numbers, and n is the number of terms.
- Steps to calculate:
- Add all the numbers in the data set (Σx).
- Count the total number of values (n).
- Divide the sum by the number of values to get the mean.
- Sum of weights = 67 + 65 + 71 + 57 + 45 = 305 kg
- Number of persons (n) = 5
- Mean = Σx / n = 305 / 5 = 61 kg
- Answer: The arithmetic mean is 61 kg.
Arithmetic Mean of Tabulated Data
For data presented in a frequency distribution table, the mean can be calculated using three methods:
- Direct Method
- Short-cut Method
- Step-deviation Method
1. Direct Method
- Uses the frequency of each value to calculate the mean.
- Formula: Mean = Σ(fx) / Σf, where f is the frequency, x is the variate, and Σf is the total frequency.
- Steps:
- Create a table with columns for variate (x), frequency (f), and product (fx).
- Multiply each variate by its frequency to get fx.
- Sum the frequencies (Σf) and the products (Σfx).
- Calculate mean by dividing Σfx by Σf.
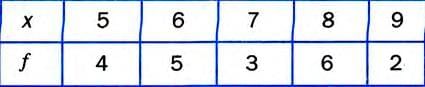 Solution:
Solution:Create a table:
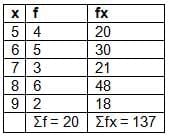
Mean = Σfx / Σf = 137 / 20 = 6.85
Answer: The mean is 6.85.2. Short-cut Method
- Simplifies calculations by using an assumed mean (A).
- Formula: Mean = A + (Σfd / Σf), where d = x - A (deviation from assumed mean).
- Steps:
- Create a table with columns for x, f, d = x - A, and fd.
- Choose an assumed mean (A), preferably a central value of x.
- Calculate deviations (d) by subtracting A from each x.
- Multiply each d by its frequency to get fd.
- Sum the frequencies (Σf) and the products (Σfd).
- Apply the formula to find the mean.
 Find the mean using the short-cut method.
Find the mean using the short-cut method.Solution:
Let assumed mean A = 67.
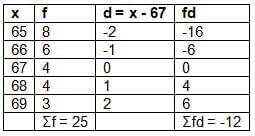
Mean = A + (Σfd / Σf) = 67 + (-12 / 25) = 67 - 0.48 = 66.52 kg
Answer: The mean weight is 66.52 kg.3. Step-deviation Method
- Further simplifies calculations by scaling deviations.
- Formula: Mean = A + (Σft / Σf) × i, where t = (x - A) / i, and i is the common factor (largest number dividing all deviations).
- Steps:
- Create a table with columns for x, f, d = x - A, t = d / i, and ft.
- Choose an assumed mean (A).
- Calculate deviations (d = x - A).
- Choose i, the largest number dividing all d values.
- Calculate t = d / i for each variate.
- Multiply each t by its frequency to get ft.
- Sum the frequencies (Σf) and the products (Σft).
- Apply the formula to find the mean.
x: 10, 30, 50, 70, 90, 110
frequency: 135, 187, 240, 273, 124, 151
Solution:
Let A = 70, i = 20 (since deviations are divisible by 20).
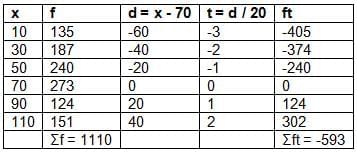
Mean = A + (Σft / Σf) × i = 70 + (-593 / 1110) × 20 = 70 - 10.68 = 59.32
Answer: The mean is 59.32.To Find Mean for Grouped Data (both continuous and discontinuous)
- Grouped data is organized into class intervals, and the mean is calculated using the mid-value of each interval.
- Three methods are used: Direct, Short-cut, and Step-deviation.
1. Direct Method
- Uses mid-values of class intervals as variates.
- Formula: Mean = Σ(fx) / Σf, where x is the mid-value of each class interval.
- Steps:
- Calculate the mid-value (x) of each class interval: x = (lower limit + upper limit) / 2.
- Create a table with columns for class interval, frequency (f), mid-value (x), and fx.
- Multiply each mid-value by its frequency to get fx.
- Sum the frequencies (Σf) and the products (Σfx).
- Calculate mean by dividing Σfx by Σf.
C.I. : 0-10, 10-20, 20-30, 30-40, 40-50
frequency: 10, 6, 8, 12, 5
Solution: C.I and f are given.

Mean = Σfx / Σf = 985 / 41 ≈ 24.02
Answer: The mean is approximately 24.02.2. Short-cut Method
- Uses an assumed mean to simplify calculations.
- Formula: Mean = A + (Σfd / Σf), where d = x - A, and x is the mid-value.
- Steps:
- Calculate mid-values (x) for each class interval.
- Choose an assumed mean (A), preferably a central mid-value.
- Calculate deviations (d = x - A).
- Multiply each d by its frequency to get fd.
- Sum the frequencies (Σf) and the products (Σfd).
- Apply the formula to find the mean.
C.I.: 35-40, 40-45, 45-50, 50-55, 55-60
frequency: 7, 6, 9, 5, 3
Solution:
Let A = 47.5.
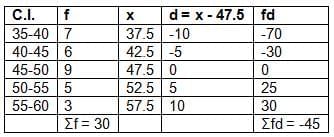
Mean = A + (Σfd / Σf) = 47.5 + (-45 / 30) = 47.5 - 1.5 = 46
Answer: The mean is 46.3. Step-deviation Method
- Uses scaled deviations to simplify calculations.
- Formula: Mean = A + (Σft / Σf) × i, where t = (x - A) / i, and i is the class size.
- Steps:
- Calculate mid-values (x) for each class interval.
- Choose an assumed mean (A).
- Calculate deviations (d = x - A).
- Choose i, the class size (upper limit - lower limit).
- Calculate t = d / i.
- Multiply each t by its frequency to get ft.
- Sum the frequencies (Σf) and the products (Σft).
- Apply the formula to find the mean.
Weight: 80-85, 85-90, 90-95, 95-100, 100-105, 105-110, 110-115
frequency: 5, 8, 10, 12, 8, 4, 3
Solution:
Let A = 97.5, i = 5.
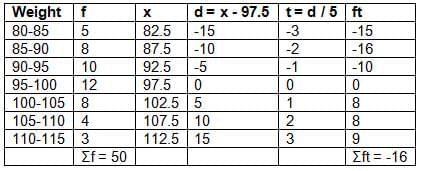
Mean = A + (Σft / Σf) × i = 97.5 + (-16 / 50) × 5 = 97.5 - 1.6 = 95.9 ≈ 96 g
Answer: The mean weight is 96 g (to the nearest gram).Median
- The median is the middle value when data is arranged in ascending or descending order.
- It divides the data into two equal parts.
Median for Raw Data
- For raw data, arrange the values in ascending or descending order and find the middle term.
- Formulas:
- If n is odd: Median = ((n + 1) / 2)th term
- If n is even: Median = [((n / 2)th term + ((n / 2) + 1)th term) / 2]
- Steps:
- Arrange data in ascending or descending order.
- Determine if n is odd or even.
- Apply the appropriate formula to find the median.
Solution:
Arrange in ascending order: 3, 4, 7, 8, 10
n = 5 (odd)
Median = ((5 + 1) / 2)th term = 3rd term = 7
Answer: The median is 7.
Median for Tabulated Data
- For frequency distribution data, use cumulative frequency to find the median.
- Steps:
- Create a cumulative frequency table.
- Find n, the total frequency.
- If n is odd, Median = ((n + 1) / 2)th term.
- Identify the value corresponding to the ((n + 1) / 2)th term using cumulative frequency.
 Find the median weight.
Find the median weight.Solution:
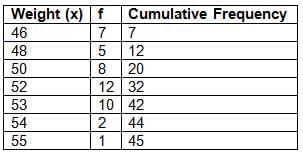
n = 45 (odd)
Median = ((45 + 1) / 2)th term = 23rd termFrom the table, the 21st to 32nd children have weight 52 kg.
Thus, the 23rd term = 52 kg.
Answer: The median weight is 52 kg.
Median for Grouped Data (both continuous and discontinuous)
- For grouped data, the median is estimated using an ogive (cumulative frequency curve).
- Steps:
- Create a cumulative frequency table.
- Plot class intervals on the x-axis and cumulative frequencies on the y-axis.
- Draw a smooth curve (ogive) through the points, starting from the lower limit of the first class to the upper limit of the last class.
- Find n, the total frequency.
- Locate the ((n / 2)th or ((n + 1) / 2)th term on the y-axis, draw a horizontal line to the ogive, then a vertical line to the x-axis to find the median.
C.I. : 0-10, 10-20, 20-30, 30-40, 40-50
frequency: 5, 7, 10, 8, 5
Solution:
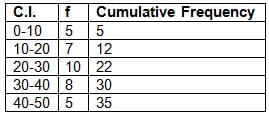
n = 35 (odd)
Median = ((35 + 1) / 2)th term = 18th termPlot points (10, 5), (20, 12), (30, 22), (40, 30), (50, 35) and draw an ogive.
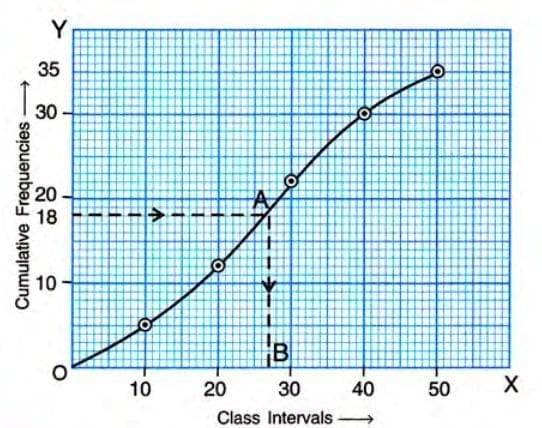 From 18 on the y-axis, draw a horizontal line to the ogive, then a vertical line to the x-axis, which gives approximately 27.
From 18 on the y-axis, draw a horizontal line to the ogive, then a vertical line to the x-axis, which gives approximately 27.Answer: The median is 27, and the median class is 20-30.
Quartiles
- Quartiles divide a data set into four equal parts when arranged in ascending order.
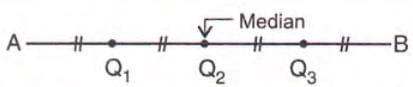
- Lower quartile (Q1): Divides the lower half of the data into two equal parts.
- Middle quartile (Q2): Same as the median.
- Upper quartile (Q3): Divides the upper half of the data into two equal parts.
- Formulas:
- If n is odd: Q1 = ((n + 1) / 4)th term, Q3 = (3(n + 1) / 4)th term
- If n is even: Q1 = (n / 4)th term, Q3 = (3n / 4)th term
- Steps:
- Arrange data in ascending order.
- Determine if n is odd or even.
- Apply the appropriate formula to find Q1 and Q3.
Solution:
Arrange in ascending order: 7, 9, 11, 13, 15, 17, 19
n = 7 (odd)
Q1 = ((7 + 1) / 4)th term = 2nd term = 9
Q3 = (3(7 + 1) / 4)th term = 6th term = 17
Inter-quartile range = Q3 - Q1 = 17 - 9 = 8
Answer: Q1 = 9, Q3 = 17, Inter-quartile range = 8.
Inter-quartile Range
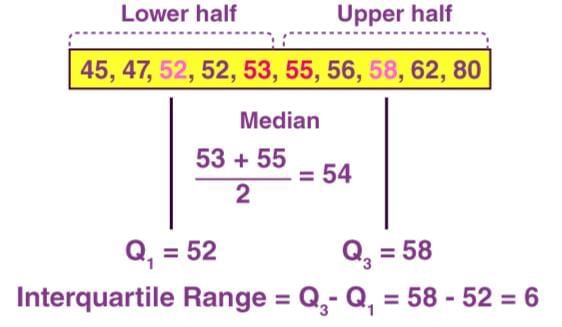
- The inter-quartile range is the difference between the upper and lower quartiles.
- Formula: Inter-quartile range = Q3 - Q1
- It measures the spread of the middle 50% of the data.
Mode
- The mode is the value that occurs most frequently in a data set.
- It represents the point of maximum frequency.
1. Mode for Raw Data
- Identify the value that appears most often in the data set.
- Steps:
- List all values in the data set.
- Count the frequency of each value.
- The value with the highest frequency is the mode.
Solution:
Count frequencies: 4 (3 times), 7 (4 times), 3 (1 time), 2 (1 time), 6 (1 time), 8 (1 time).
The value 7 occurs most frequently.
Answer: The mode is 7.
2. Mode for Tabulated Data
Identify the value with the highest frequency in the frequency distribution table.- Steps:
- Examine the frequency column in the table.
- The value (x) corresponding to the highest frequency is the mode.
 Solution:
Solution:The highest frequency is 17, corresponding to the number 13.
Answer: The mode is 13.
3. Mode for Grouped Data
- For grouped data, the mode is estimated using a histogram.
- The modal class is the class interval with the highest frequency.
- Steps:
- Draw a histogram of the frequency distribution.
- Identify the rectangle with the highest height (modal class).
- Draw two diagonal lines from the upper corners of the adjacent rectangles to intersect within the modal class rectangle.
- Draw a perpendicular line from the intersection point to the x-axis.
- The value on the x-axis is the mode.
 Solution:
Solution:The modal class is 50-60 (frequency = 11).
Using a histogram, draw diagonals from the upper corners of the 40-50 and 60-70 rectangles to intersect within the 50-60 rectangle. Drop a perpendicular to the x-axis, which gives approximately 53.
 Answer: The mode is 53, and the modal class is 50-60.
Answer: The mode is 53, and the modal class is 50-60.|
74 videos|328 docs|30 tests
|
FAQs on Measures of Central Tendency Chapter Notes - Mathematics Class 10 ICSE
| 1. What is the arithmetic mean, and how is it calculated for ungrouped data? |  |
| 2. How do you find the arithmetic mean for grouped data? |  |
| 3. What is the median, and how is it determined for raw data? |  |
| 4. How can the median be calculated for grouped data? |  |
| 5. What are quartiles, and how do you calculate the inter-quartile range? |  |
















